beginner/chatbot_tutorial

Run in Google Colab

Colab

Download Notebook

Notebook

View on GitHub

GitHub

Chatbot Tutorial

Created On: Aug 14, 2018 | Last Updated: Jan 24, 2025 | Last Verified: Nov 05, 2024

Author: Matthew Inkawhich

In this tutorial, we explore a fun and interesting use-case of recurrent sequence-to-sequence models. We will train a simple chatbot using movie scripts from the Cornell Movie-Dialogs Corpus.

Conversational models are a hot topic in artificial intelligence research. Chatbots can be found in a variety of settings, including customer service applications and online helpdesks. These bots are often powered by retrieval-based models, which output predefined responses to questions of certain forms. In a highly restricted domain like a company’s IT helpdesk, these models may be sufficient, however, they are not robust enough for more general use-cases. Teaching a machine to carry out a meaningful conversation with a human in multiple domains is a research question that is far from solved. Recently, the deep learning boom has allowed for powerful generative models like Google’s Neural Conversational Model, which marks a large step towards multi-domain generative conversational models. In this tutorial, we will implement this kind of model in PyTorch.

> hello?
Bot: hello .
> where am I?
Bot: you re in a hospital .
> who are you?
Bot: i m a lawyer .
> how are you doing?
Bot: i m fine .
> are you my friend?
Bot: no .
> you're under arrest
Bot: i m trying to help you !
> i'm just kidding
Bot: i m sorry .
> where are you from?
Bot: san francisco .
> it's time for me to leave
Bot: i know .
> goodbye
Bot: goodbye .

Tutorial Highlights

• Handle loading and preprocessing of Cornell Movie-Dialogs Corpus dataset

• Implement a sequence-to-sequence model with Luong attention mechanism(s)

• Jointly train encoder and decoder models using mini-batches

• Implement greedy-search decoding module

• Interact with trained chatbot

Acknowledgments

This tutorial borrows code from the following sources:

1. Yuan-Kuei Wu’s pytorch-chatbot implementation: ywk991112/pytorch-chatbot

2. Sean Robertson’s practical-pytorch seq2seq-translation example: spro/practical-pytorch

3. FloydHub Cornell Movie Corpus preprocessing code: floydhub/textutil-preprocess-cornell-movie-corpus

Preparations

To get started, download the Movie-Dialogs Corpus zip file.

# and put in a ``data/`` directory under the current directory.
#
# After that, let’s import some necessities.
#

import torch
from torch.jit import script, trace
import torch.nn as nn
from torch import optim
import torch.nn.functional as F
import csv
import random
import re
import os
import unicodedata
import codecs
from io import open
import itertools
import math
import json


# If the current `accelerator <https://pytorch.org/docs/stable/torch.html#accelerators>`__ is available,
# we will use it. Otherwise, we use the CPU.
device = torch.accelerator.current_accelerator().type if torch.accelerator.is_available() else "cpu"
print(f"Using {device} device")

Using cuda device

Load & Preprocess Data

The next step is to reformat our data file and load the data into structures that we can work with.

The Cornell Movie-Dialogs Corpus is a rich dataset of movie character dialog:

• 220,579 conversational exchanges between 10,292 pairs of movie characters

• 9,035 characters from 617 movies

• 304,713 total utterances

This dataset is large and diverse, and there is a great variation of language formality, time periods, sentiment, etc. Our hope is that this diversity makes our model robust to many forms of inputs and queries.

First, we’ll take a look at some lines of our datafile to see the original format.

corpus_name = "movie-corpus"
corpus = os.path.join("data", corpus_name)

def printLines(file, n=10):
    with open(file, 'rb') as datafile:
        lines = datafile.readlines()
    for line in lines[:n]:
        print(line)

printLines(os.path.join(corpus, "utterances.jsonl"))

b'{"id": "L1045", "conversation_id": "L1044", "text": "They do not!", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "They", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "not", "tag": "RB", "dep": "neg", "up": 1, "dn": []}, {"tok": "!", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": "L1044", "timestamp": null, "vectors": []}\n'
b'{"id": "L1044", "conversation_id": "L1044", "text": "They do to!", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "They", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "to", "tag": "TO", "dep": "dobj", "up": 1, "dn": []}, {"tok": "!", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L985", "conversation_id": "L984", "text": "I hope so.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "I", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "hope", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "so", "tag": "RB", "dep": "advmod", "up": 1, "dn": []}, {"tok": ".", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": "L984", "timestamp": null, "vectors": []}\n'
b'{"id": "L984", "conversation_id": "L984", "text": "She okay?", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "She", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "okay", "tag": "RB", "dep": "ROOT", "dn": [0, 2]}, {"tok": "?", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L925", "conversation_id": "L924", "text": "Let\'s go.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Let", "tag": "VB", "dep": "ROOT", "dn": [2, 3]}, {"tok": "\'s", "tag": "PRP", "dep": "nsubj", "up": 2, "dn": []}, {"tok": "go", "tag": "VB", "dep": "ccomp", "up": 0, "dn": [1]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 0, "dn": []}]}]}, "reply-to": "L924", "timestamp": null, "vectors": []}\n'
b'{"id": "L924", "conversation_id": "L924", "text": "Wow", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Wow", "tag": "UH", "dep": "ROOT", "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L872", "conversation_id": "L870", "text": "Okay -- you\'re gonna need to learn how to lie.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 4, "toks": [{"tok": "Okay", "tag": "UH", "dep": "intj", "up": 4, "dn": []}, {"tok": "--", "tag": ":", "dep": "punct", "up": 4, "dn": []}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 4, "dn": []}, {"tok": "\'re", "tag": "VBP", "dep": "aux", "up": 4, "dn": []}, {"tok": "gon", "tag": "VBG", "dep": "ROOT", "dn": [0, 1, 2, 3, 6, 12]}, {"tok": "na", "tag": "TO", "dep": "aux", "up": 6, "dn": []}, {"tok": "need", "tag": "VB", "dep": "xcomp", "up": 4, "dn": [5, 8]}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 8, "dn": []}, {"tok": "learn", "tag": "VB", "dep": "xcomp", "up": 6, "dn": [7, 11]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 11, "dn": []}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 11, "dn": []}, {"tok": "lie", "tag": "VB", "dep": "xcomp", "up": 8, "dn": [9, 10]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 4, "dn": []}]}]}, "reply-to": "L871", "timestamp": null, "vectors": []}\n'
b'{"id": "L871", "conversation_id": "L870", "text": "No", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "No", "tag": "UH", "dep": "ROOT", "dn": []}]}]}, "reply-to": "L870", "timestamp": null, "vectors": []}\n'
b'{"id": "L870", "conversation_id": "L870", "text": "I\'m kidding.  You know how sometimes you just become this \\"persona\\"?  And you don\'t know how to quit?", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 2, "toks": [{"tok": "I", "tag": "PRP", "dep": "nsubj", "up": 2, "dn": []}, {"tok": "\'m", "tag": "VBP", "dep": "aux", "up": 2, "dn": []}, {"tok": "kidding", "tag": "VBG", "dep": "ROOT", "dn": [0, 1, 3]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 2, "dn": [4]}, {"tok": " ", "tag": "_SP", "dep": "", "up": 3, "dn": []}]}, {"rt": 1, "toks": [{"tok": "You", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "know", "tag": "VBP", "dep": "ROOT", "dn": [0, 6, 11]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 3, "dn": []}, {"tok": "sometimes", "tag": "RB", "dep": "advmod", "up": 6, "dn": [2]}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 6, "dn": []}, {"tok": "just", "tag": "RB", "dep": "advmod", "up": 6, "dn": []}, {"tok": "become", "tag": "VBP", "dep": "ccomp", "up": 1, "dn": [3, 4, 5, 9]}, {"tok": "this", "tag": "DT", "dep": "det", "up": 9, "dn": []}, {"tok": "\\"", "tag": "``", "dep": "punct", "up": 9, "dn": []}, {"tok": "persona", "tag": "NN", "dep": "attr", "up": 6, "dn": [7, 8, 10]}, {"tok": "\\"", "tag": "\'\'", "dep": "punct", "up": 9, "dn": []}, {"tok": "?", "tag": ".", "dep": "punct", "up": 1, "dn": [12]}, {"tok": " ", "tag": "_SP", "dep": "", "up": 11, "dn": []}]}, {"rt": 4, "toks": [{"tok": "And", "tag": "CC", "dep": "cc", "up": 4, "dn": []}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 4, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "aux", "up": 4, "dn": []}, {"tok": "n\'t", "tag": "RB", "dep": "neg", "up": 4, "dn": []}, {"tok": "know", "tag": "VB", "dep": "ROOT", "dn": [0, 1, 2, 3, 7, 8]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 7, "dn": []}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 7, "dn": []}, {"tok": "quit", "tag": "VB", "dep": "xcomp", "up": 4, "dn": [5, 6]}, {"tok": "?", "tag": ".", "dep": "punct", "up": 4, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L869", "conversation_id": "L866", "text": "Like my fear of wearing pastels?", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Like", "tag": "IN", "dep": "ROOT", "dn": [2, 6]}, {"tok": "my", "tag": "PRP$", "dep": "poss", "up": 2, "dn": []}, {"tok": "fear", "tag": "NN", "dep": "pobj", "up": 0, "dn": [1, 3]}, {"tok": "of", "tag": "IN", "dep": "prep", "up": 2, "dn": [4]}, {"tok": "wearing", "tag": "VBG", "dep": "pcomp", "up": 3, "dn": [5]}, {"tok": "pastels", "tag": "NNS", "dep": "dobj", "up": 4, "dn": []}, {"tok": "?", "tag": ".", "dep": "punct", "up": 0, "dn": []}]}]}, "reply-to": "L868", "timestamp": null, "vectors": []}\n'

Create formatted data file

For convenience, we’ll create a nicely formatted data file in which each line contains a tab-separated query sentence and a response sentence pair.

The following functions facilitate the parsing of the raw utterances.jsonl data file.

• loadLinesAndConversations splits each line of the file into a dictionary of lines with fields: lineID, characterID, and text and then groups them into conversations with fields: conversationID, movieID, and lines.

• extractSentencePairs extracts pairs of sentences from conversations

# Splits each line of the file to create lines and conversations
def loadLinesAndConversations(fileName):
    lines = {}
    conversations = {}
    with open(fileName, 'r', encoding='iso-8859-1') as f:
        for line in f:
            lineJson = json.loads(line)
            # Extract fields for line object
            lineObj = {}
            lineObj["lineID"] = lineJson["id"]
            lineObj["characterID"] = lineJson["speaker"]
            lineObj["text"] = lineJson["text"]
            lines[lineObj['lineID']] = lineObj

            # Extract fields for conversation object
            if lineJson["conversation_id"] not in conversations:
                convObj = {}
                convObj["conversationID"] = lineJson["conversation_id"]
                convObj["movieID"] = lineJson["meta"]["movie_id"]
                convObj["lines"] = [lineObj]
            else:
                convObj = conversations[lineJson["conversation_id"]]
                convObj["lines"].insert(0, lineObj)
            conversations[convObj["conversationID"]] = convObj

    return lines, conversations


# Extracts pairs of sentences from conversations
def extractSentencePairs(conversations):
    qa_pairs = []
    for conversation in conversations.values():
        # Iterate over all the lines of the conversation
        for i in range(len(conversation["lines"]) - 1):  # We ignore the last line (no answer for it)
            inputLine = conversation["lines"][i]["text"].strip()
            targetLine = conversation["lines"][i+1]["text"].strip()
            # Filter wrong samples (if one of the lists is empty)
            if inputLine and targetLine:
                qa_pairs.append([inputLine, targetLine])
    return qa_pairs

Now we’ll call these functions and create the file. We’ll call it formatted_movie_lines.txt.

# Define path to new file
datafile = os.path.join(corpus, "formatted_movie_lines.txt")

delimiter = '\t'
# Unescape the delimiter
delimiter = str(codecs.decode(delimiter, "unicode_escape"))

# Initialize lines dict and conversations dict
lines = {}
conversations = {}
# Load lines and conversations
print("\nProcessing corpus into lines and conversations...")
lines, conversations = loadLinesAndConversations(os.path.join(corpus, "utterances.jsonl"))

# Write new csv file
print("\nWriting newly formatted file...")
with open(datafile, 'w', encoding='utf-8') as outputfile:
    writer = csv.writer(outputfile, delimiter=delimiter, lineterminator='\n')
    for pair in extractSentencePairs(conversations):
        writer.writerow(pair)

# Print a sample of lines
print("\nSample lines from file:")
printLines(datafile)

Processing corpus into lines and conversations...

Writing newly formatted file...

Sample lines from file:
b'They do to!\tThey do not!\n'
b'She okay?\tI hope so.\n'
b"Wow\tLet's go.\n"
b'"I\'m kidding.  You know how sometimes you just become this ""persona""?  And you don\'t know how to quit?"\tNo\n'
b"No\tOkay -- you're gonna need to learn how to lie.\n"
b"I figured you'd get to the good stuff eventually.\tWhat good stuff?\n"
b'What good stuff?\t"The ""real you""."\n'
b'"The ""real you""."\tLike my fear of wearing pastels?\n'
b'do you listen to this crap?\tWhat crap?\n'
b"What crap?\tMe.  This endless ...blonde babble. I'm like, boring myself.\n"

Load and trim data

Our next order of business is to create a vocabulary and load query/response sentence pairs into memory.

Note that we are dealing with sequences of words, which do not have an implicit mapping to a discrete numerical space. Thus, we must create one by mapping each unique word that we encounter in our dataset to an index value.

For this we define a Voc class, which keeps a mapping from words to indexes, a reverse mapping of indexes to words, a count of each word and a total word count. The class provides methods for adding a word to the vocabulary (addWord), adding all words in a sentence (addSentence) and trimming infrequently seen words (trim). More on trimming later.

# Default word tokens
PAD_token = 0  # Used for padding short sentences
SOS_token = 1  # Start-of-sentence token
EOS_token = 2  # End-of-sentence token

class Voc:
    def __init__(self, name):
        self.name = name
        self.trimmed = False
        self.word2index = {}
        self.word2count = {}
        self.index2word = {PAD_token: "PAD", SOS_token: "SOS", EOS_token: "EOS"}
        self.num_words = 3  # Count SOS, EOS, PAD

    def addSentence(self, sentence):
        for word in sentence.split(' '):
            self.addWord(word)

    def addWord(self, word):
        if word not in self.word2index:
            self.word2index[word] = self.num_words
            self.word2count[word] = 1
            self.index2word[self.num_words] = word
            self.num_words += 1
        else:
            self.word2count[word] += 1

    # Remove words below a certain count threshold
    def trim(self, min_count):
        if self.trimmed:
            return
        self.trimmed = True

        keep_words = []

        for k, v in self.word2count.items():
            if v >= min_count:
                keep_words.append(k)

        print('keep_words {} / {} = {:.4f}'.format(
            len(keep_words), len(self.word2index), len(keep_words) / len(self.word2index)
        ))

        # Reinitialize dictionaries
        self.word2index = {}
        self.word2count = {}
        self.index2word = {PAD_token: "PAD", SOS_token: "SOS", EOS_token: "EOS"}
        self.num_words = 3 # Count default tokens

        for word in keep_words:
            self.addWord(word)

Now we can assemble our vocabulary and query/response sentence pairs. Before we are ready to use this data, we must perform some preprocessing.

First, we must convert the Unicode strings to ASCII using unicodeToAscii. Next, we should convert all letters to lowercase and trim all non-letter characters except for basic punctuation (normalizeString). Finally, to aid in training convergence, we will filter out sentences with length greater than the MAX_LENGTH threshold (filterPairs).

MAX_LENGTH = 10  # Maximum sentence length to consider

# Turn a Unicode string to plain ASCII, thanks to
# https://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
    )

# Lowercase, trim, and remove non-letter characters
def normalizeString(s):
    s = unicodeToAscii(s.lower().strip())
    s = re.sub(r"([.!?])", r" \1", s)
    s = re.sub(r"[^a-zA-Z.!?]+", r" ", s)
    s = re.sub(r"\s+", r" ", s).strip()
    return s

# Read query/response pairs and return a voc object
def readVocs(datafile, corpus_name):
    print("Reading lines...")
    # Read the file and split into lines
    lines = open(datafile, encoding='utf-8').\
        read().strip().split('\n')
    # Split every line into pairs and normalize
    pairs = [[normalizeString(s) for s in l.split('\t')] for l in lines]
    voc = Voc(corpus_name)
    return voc, pairs

# Returns True if both sentences in a pair 'p' are under the MAX_LENGTH threshold
def filterPair(p):
    # Input sequences need to preserve the last word for EOS token
    return len(p[0].split(' ')) < MAX_LENGTH and len(p[1].split(' ')) < MAX_LENGTH

# Filter pairs using the ``filterPair`` condition
def filterPairs(pairs):
    return [pair for pair in pairs if filterPair(pair)]

# Using the functions defined above, return a populated voc object and pairs list
def loadPrepareData(corpus, corpus_name, datafile, save_dir):
    print("Start preparing training data ...")
    voc, pairs = readVocs(datafile, corpus_name)
    print("Read {!s} sentence pairs".format(len(pairs)))
    pairs = filterPairs(pairs)
    print("Trimmed to {!s} sentence pairs".format(len(pairs)))
    print("Counting words...")
    for pair in pairs:
        voc.addSentence(pair[0])
        voc.addSentence(pair[1])
    print("Counted words:", voc.num_words)
    return voc, pairs


# Load/Assemble voc and pairs
save_dir = os.path.join("data", "save")
voc, pairs = loadPrepareData(corpus, corpus_name, datafile, save_dir)
# Print some pairs to validate
print("\npairs:")
for pair in pairs[:10]:
    print(pair)

Start preparing training data ...
Reading lines...
Read 221282 sentence pairs
Trimmed to 64313 sentence pairs
Counting words...
Counted words: 18082

pairs:
['they do to !', 'they do not !']
['she okay ?', 'i hope so .']
['wow', 'let s go .']
['what good stuff ?', 'the real you .']
['the real you .', 'like my fear of wearing pastels ?']
['do you listen to this crap ?', 'what crap ?']
['well no . . .', 'then that s all you had to say .']
['then that s all you had to say .', 'but']
['but', 'you always been this selfish ?']
['have fun tonight ?', 'tons']

Another tactic that is beneficial to achieving faster convergence during training is trimming rarely used words out of our vocabulary. Decreasing the feature space will also soften the difficulty of the function that the model must learn to approximate. We will do this as a two-step process:

1. Trim words used under MIN_COUNT threshold using the voc.trim function.

2. Filter out pairs with trimmed words.

MIN_COUNT = 3    # Minimum word count threshold for trimming

def trimRareWords(voc, pairs, MIN_COUNT):
    # Trim words used under the MIN_COUNT from the voc
    voc.trim(MIN_COUNT)
    # Filter out pairs with trimmed words
    keep_pairs = []
    for pair in pairs:
        input_sentence = pair[0]
        output_sentence = pair[1]
        keep_input = True
        keep_output = True
        # Check input sentence
        for word in input_sentence.split(' '):
            if word not in voc.word2index:
                keep_input = False
                break
        # Check output sentence
        for word in output_sentence.split(' '):
            if word not in voc.word2index:
                keep_output = False
                break

        # Only keep pairs that do not contain trimmed word(s) in their input or output sentence
        if keep_input and keep_output:
            keep_pairs.append(pair)

    print("Trimmed from {} pairs to {}, {:.4f} of total".format(len(pairs), len(keep_pairs), len(keep_pairs) / len(pairs)))
    return keep_pairs


# Trim voc and pairs
pairs = trimRareWords(voc, pairs, MIN_COUNT)

keep_words 7833 / 18079 = 0.4333
Trimmed from 64313 pairs to 53131, 0.8261 of total

Prepare Data for Models

Although we have put a great deal of effort into preparing and massaging our data into a nice vocabulary object and list of sentence pairs, our models will ultimately expect numerical torch tensors as inputs. One way to prepare the processed data for the models can be found in the seq2seq translation tutorial. In that tutorial, we use a batch size of 1, meaning that all we have to do is convert the words in our sentence pairs to their corresponding indexes from the vocabulary and feed this to the models.

However, if you’re interested in speeding up training and/or would like to leverage GPU parallelization capabilities, you will need to train with mini-batches.

Using mini-batches also means that we must be mindful of the variation of sentence length in our batches. To accommodate sentences of different sizes in the same batch, we will make our batched input tensor of shape (max_length, batch_size), where sentences shorter than the max_length are zero padded after an EOS_token.

If we simply convert our English sentences to tensors by converting words to their indexes(indexesFromSentence) and zero-pad, our tensor would have shape (batch_size, max_length) and indexing the first dimension would return a full sequence across all time-steps. However, we need to be able to index our batch along time, and across all sequences in the batch. Therefore, we transpose our input batch shape to (max_length, batch_size), so that indexing across the first dimension returns a time step across all sentences in the batch. We handle this transpose implicitly in the zeroPadding function.

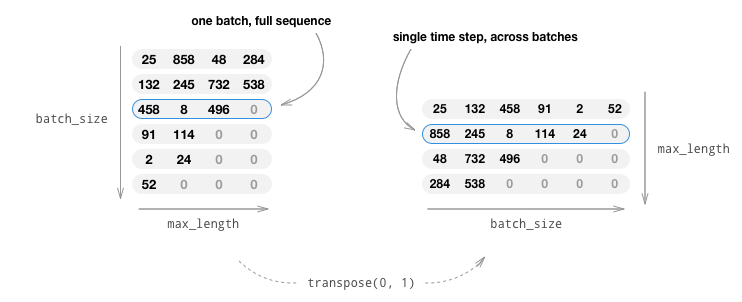
The inputVar function handles the process of converting sentences to tensor, ultimately creating a correctly shaped zero-padded tensor. It also returns a tensor of lengths for each of the sequences in the batch which will be passed to our decoder later.

The outputVar function performs a similar function to inputVar, but instead of returning a lengths tensor, it returns a binary mask tensor and a maximum target sentence length. The binary mask tensor has the same shape as the output target tensor, but every element that is a PAD_token is 0 and all others are 1.

batch2TrainData simply takes a bunch of pairs and returns the input and target tensors using the aforementioned functions.

def indexesFromSentence(voc, sentence):
    return [voc.word2index[word] for word in sentence.split(' ')] + [EOS_token]


def zeroPadding(l, fillvalue=PAD_token):
    return list(itertools.zip_longest(*l, fillvalue=fillvalue))

def binaryMatrix(l, value=PAD_token):
    m = []
    for i, seq in enumerate(l):
        m.append([])
        for token in seq:
            if token == PAD_token:
                m[i].append(0)
            else:
                m[i].append(1)
    return m

# Returns padded input sequence tensor and lengths
def inputVar(l, voc):
    indexes_batch = [indexesFromSentence(voc, sentence) for sentence in l]
    lengths = torch.tensor([len(indexes) for indexes in indexes_batch])
    padList = zeroPadding(indexes_batch)
    padVar = torch.LongTensor(padList)
    return padVar, lengths

# Returns padded target sequence tensor, padding mask, and max target length
def outputVar(l, voc):
    indexes_batch = [indexesFromSentence(voc, sentence) for sentence in l]
    max_target_len = max([len(indexes) for indexes in indexes_batch])
    padList = zeroPadding(indexes_batch)
    mask = binaryMatrix(padList)
    mask = torch.BoolTensor(mask)
    padVar = torch.LongTensor(padList)
    return padVar, mask, max_target_len

# Returns all items for a given batch of pairs
def batch2TrainData(voc, pair_batch):
    pair_batch.sort(key=lambda x: len(x[0].split(" ")), reverse=True)
    input_batch, output_batch = [], []
    for pair in pair_batch:
        input_batch.append(pair[0])
        output_batch.append(pair[1])
    inp, lengths = inputVar(input_batch, voc)
    output, mask, max_target_len = outputVar(output_batch, voc)
    return inp, lengths, output, mask, max_target_len


# Example for validation
small_batch_size = 5
batches = batch2TrainData(voc, [random.choice(pairs) for _ in range(small_batch_size)])
input_variable, lengths, target_variable, mask, max_target_len = batches

print("input_variable:", input_variable)
print("lengths:", lengths)
print("target_variable:", target_variable)
print("mask:", mask)
print("max_target_len:", max_target_len)

input_variable: tensor([[ 223, 3944,    8,   22,  774],
        [  10,   11,   95,  294,  140],
        [  14,  449,   20,  140,   14],
        [  14,  410,   35,    2,    2],
        [  14,    5,   14,    0,    0],
        [  14,   24,    2,    0,    0],
        [3191,   14,    0,    0,    0],
        [  10,    2,    0,    0,    0],
        [   2,    0,    0,    0,    0]])
lengths: tensor([9, 8, 6, 4, 4])
target_variable: tensor([[ 284,   19,    7,   34,  128],
        [ 112,   90,    5,  211,   14],
        [  14,   85,   72,   85,    2],
        [   2, 3049,   14,    2,    0],
        [   0,   10,    2,    0,    0],
        [   0,    2,    0,    0,    0]])
mask: tensor([[ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True,  True,  True,  True, False],
        [False,  True,  True, False, False],
        [False,  True, False, False, False]])
max_target_len: 6

Define Models

Seq2Seq Model

The brains of our chatbot is a sequence-to-sequence (seq2seq) model. The goal of a seq2seq model is to take a variable-length sequence as an input, and return a variable-length sequence as an output using a fixed-sized model.

Sutskever et al. discovered that by using two separate recurrent neural nets together, we can accomplish this task. One RNN acts as an encoder, which encodes a variable length input sequence to a fixed-length context vector. In theory, this context vector (the final hidden layer of the RNN) will contain semantic information about the query sentence that is input to the bot. The second RNN is a decoder, which takes an input word and the context vector, and returns a guess for the next word in the sequence and a hidden state to use in the next iteration.

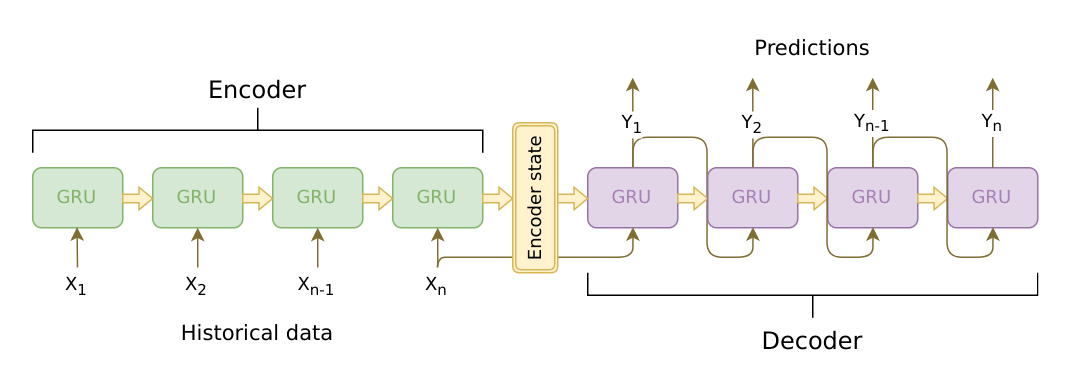
Image source: https://jeddy92.github.io/JEddy92.github.io/ts_seq2seq_intro/

Encoder

The encoder RNN iterates through the input sentence one token (e.g. word) at a time, at each time step outputting an “output” vector and a “hidden state” vector. The hidden state vector is then passed to the next time step, while the output vector is recorded. The encoder transforms the context it saw at each point in the sequence into a set of points in a high-dimensional space, which the decoder will use to generate a meaningful output for the given task.

At the heart of our encoder is a multi-layered Gated Recurrent Unit, invented by Cho et al. in 2014. We will use a bidirectional variant of the GRU, meaning that there are essentially two independent RNNs: one that is fed the input sequence in normal sequential order, and one that is fed the input sequence in reverse order. The outputs of each network are summed at each time step. Using a bidirectional GRU will give us the advantage of encoding both past and future contexts.

Bidirectional RNN:

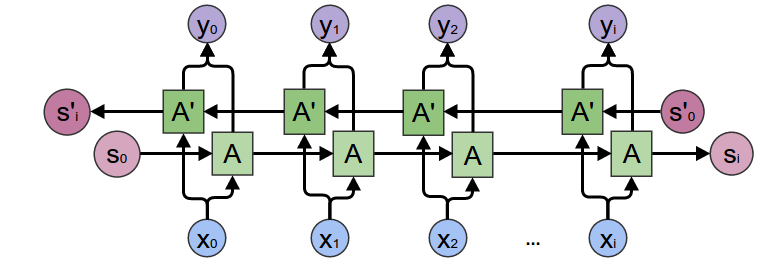
Image source: https://colah.github.io/posts/2015-09-NN-Types-FP/

Note that an embedding layer is used to encode our word indices in an arbitrarily sized feature space. For our models, this layer will map each word to a feature space of size hidden_size. When trained, these values should encode semantic similarity between similar meaning words.

Finally, if passing a padded batch of sequences to an RNN module, we must pack and unpack padding around the RNN pass using nn.utils.rnn.pack_padded_sequence and nn.utils.rnn.pad_packed_sequence respectively.

Computation Graph:

1. Convert word indexes to embeddings.

2. Pack padded batch of sequences for RNN module.

3. Forward pass through GRU.

4. Unpack padding.

5. Sum bidirectional GRU outputs.

6. Return output and final hidden state.

Inputs:

• input_seq: batch of input sentences; shape=(max_length, batch_size)

• input_lengths: list of sentence lengths corresponding to each sentence in the batch; shape=(batch_size)

• hidden: hidden state; shape=(n_layers x num_directions, batch_size, hidden_size)

Outputs:

• outputs: output features from the last hidden layer of the GRU (sum of bidirectional outputs); shape=(max_length, batch_size, hidden_size)

• hidden: updated hidden state from GRU; shape=(n_layers x num_directions, batch_size, hidden_size)

class EncoderRNN(nn.Module):
    def __init__(self, hidden_size, embedding, n_layers=1, dropout=0):
        super(EncoderRNN, self).__init__()
        self.n_layers = n_layers
        self.hidden_size = hidden_size
        self.embedding = embedding

        # Initialize GRU; the input_size and hidden_size parameters are both set to 'hidden_size'
        #   because our input size is a word embedding with number of features == hidden_size
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers,
                          dropout=(0 if n_layers == 1 else dropout), bidirectional=True)

    def forward(self, input_seq, input_lengths, hidden=None):
        # Convert word indexes to embeddings
        embedded = self.embedding(input_seq)
        # Pack padded batch of sequences for RNN module
        packed = nn.utils.rnn.pack_padded_sequence(embedded, input_lengths)
        # Forward pass through GRU
        outputs, hidden = self.gru(packed, hidden)
        # Unpack padding
        outputs, _ = nn.utils.rnn.pad_packed_sequence(outputs)
        # Sum bidirectional GRU outputs
        outputs = outputs[:, :, :self.hidden_size] + outputs[:, : ,self.hidden_size:]
        # Return output and final hidden state
        return outputs, hidden

Decoder

The decoder RNN generates the response sentence in a token-by-token fashion. It uses the encoder’s context vectors, and internal hidden states to generate the next word in the sequence. It continues generating words until it outputs an EOS_token, representing the end of the sentence. A common problem with a vanilla seq2seq decoder is that if we rely solely on the context vector to encode the entire input sequence’s meaning, it is likely that we will have information loss. This is especially the case when dealing with long input sequences, greatly limiting the capability of our decoder.

To combat this, Bahdanau et al. created an “attention mechanism” that allows the decoder to pay attention to certain parts of the input sequence, rather than using the entire fixed context at every step.

At a high level, attention is calculated using the decoder’s current hidden state and the encoder’s outputs. The output attention weights have the same shape as the input sequence, allowing us to multiply them by the encoder outputs, giving us a weighted sum which indicates the parts of encoder output to pay attention to. Sean Robertson’s figure describes this very well:

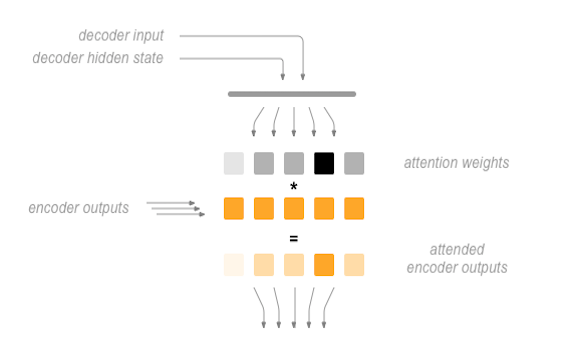
Luong et al. improved upon Bahdanau et al.’s groundwork by creating “Global attention”. The key difference is that with “Global attention”, we consider all of the encoder’s hidden states, as opposed to Bahdanau et al.’s “Local attention”, which only considers the encoder’s hidden state from the current time step. Another difference is that with “Global attention”, we calculate attention weights, or energies, using the hidden state of the decoder from the current time step only. Bahdanau et al.’s attention calculation requires knowledge of the decoder’s state from the previous time step. Also, Luong et al. provides various methods to calculate the attention energies between the encoder output and decoder output which are called “score functions”:

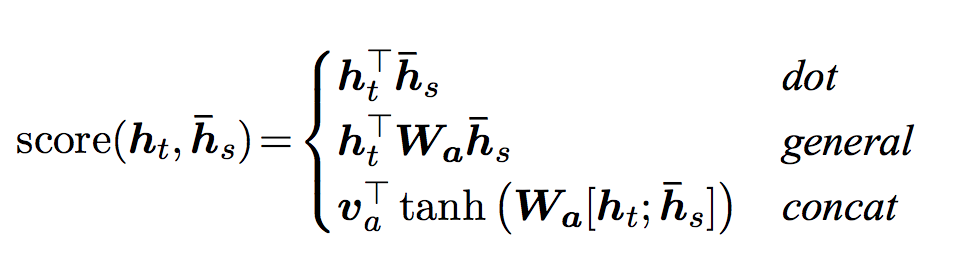
where \(h_t\) = current target decoder state and \(\bar{h}_s\) = all encoder states.

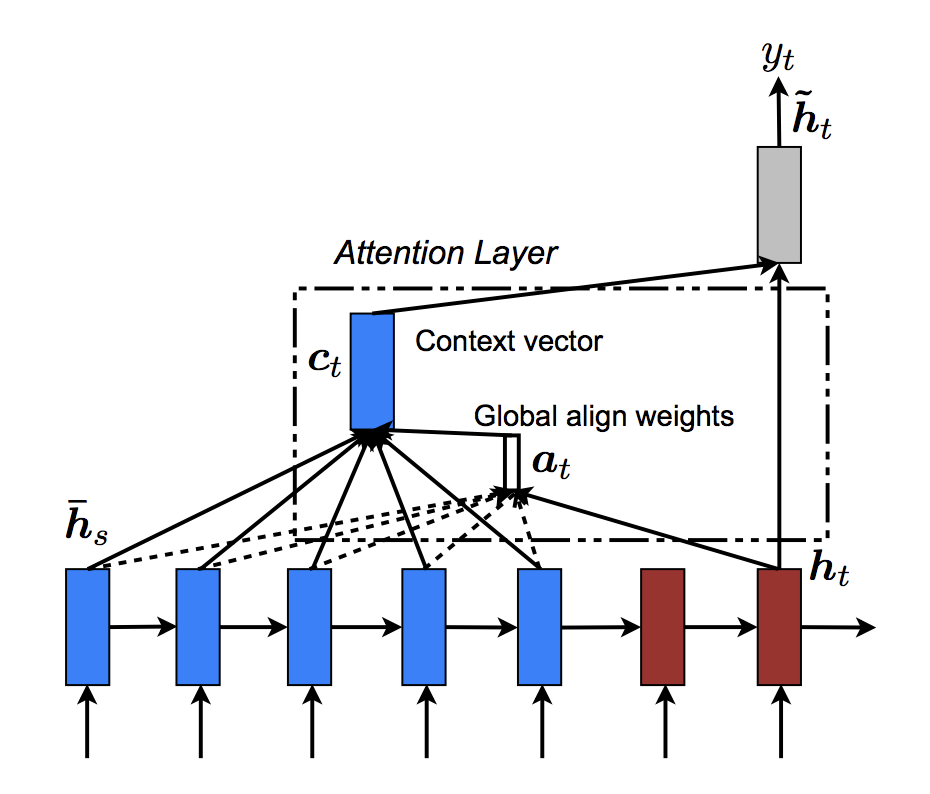
Overall, the Global attention mechanism can be summarized by the following figure. Note that we will implement the “Attention Layer” as a separate nn.Module called Attn. The output of this module is a softmax normalized weights tensor of shape (batch_size, 1, max_length).

# Luong attention layer
class Attn(nn.Module):
    def __init__(self, method, hidden_size):
        super(Attn, self).__init__()
        self.method = method
        if self.method not in ['dot', 'general', 'concat']:
            raise ValueError(self.method, "is not an appropriate attention method.")
        self.hidden_size = hidden_size
        if self.method == 'general':
            self.attn = nn.Linear(self.hidden_size, hidden_size)
        elif self.method == 'concat':
            self.attn = nn.Linear(self.hidden_size * 2, hidden_size)
            self.v = nn.Parameter(torch.FloatTensor(hidden_size))

    def dot_score(self, hidden, encoder_output):
        return torch.sum(hidden * encoder_output, dim=2)

    def general_score(self, hidden, encoder_output):
        energy = self.attn(encoder_output)
        return torch.sum(hidden * energy, dim=2)

    def concat_score(self, hidden, encoder_output):
        energy = self.attn(torch.cat((hidden.expand(encoder_output.size(0), -1, -1), encoder_output), 2)).tanh()
        return torch.sum(self.v * energy, dim=2)

    def forward(self, hidden, encoder_outputs):
        # Calculate the attention weights (energies) based on the given method
        if self.method == 'general':
            attn_energies = self.general_score(hidden, encoder_outputs)
        elif self.method == 'concat':
            attn_energies = self.concat_score(hidden, encoder_outputs)
        elif self.method == 'dot':
            attn_energies = self.dot_score(hidden, encoder_outputs)

        # Transpose max_length and batch_size dimensions
        attn_energies = attn_energies.t()

        # Return the softmax normalized probability scores (with added dimension)
        return F.softmax(attn_energies, dim=1).unsqueeze(1)

Now that we have defined our attention submodule, we can implement the actual decoder model. For the decoder, we will manually feed our batch one time step at a time. This means that our embedded word tensor and GRU output will both have shape (1, batch_size, hidden_size).

Computation Graph:

1. Get embedding of current input word.

2. Forward through unidirectional GRU.

3. Calculate attention weights from the current GRU output from (2).

4. Multiply attention weights to encoder outputs to get new “weighted sum” context vector.

5. Concatenate weighted context vector and GRU output using Luong eq. 5.

6. Predict next word using Luong eq. 6 (without softmax).

7. Return output and final hidden state.

Inputs:

• input_step: one time step (one word) of input sequence batch; shape=(1, batch_size)

• last_hidden: final hidden layer of GRU; shape=(n_layers x num_directions, batch_size, hidden_size)

• encoder_outputs: encoder model’s output; shape=(max_length, batch_size, hidden_size)

Outputs:

• output: softmax normalized tensor giving probabilities of each word being the correct next word in the decoded sequence; shape=(batch_size, voc.num_words)

• hidden: final hidden state of GRU; shape=(n_layers x num_directions, batch_size, hidden_size)

class LuongAttnDecoderRNN(nn.Module):
    def __init__(self, attn_model, embedding, hidden_size, output_size, n_layers=1, dropout=0.1):
        super(LuongAttnDecoderRNN, self).__init__()

        # Keep for reference
        self.attn_model = attn_model
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.n_layers = n_layers
        self.dropout = dropout

        # Define layers
        self.embedding = embedding
        self.embedding_dropout = nn.Dropout(dropout)
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers, dropout=(0 if n_layers == 1 else dropout))
        self.concat = nn.Linear(hidden_size * 2, hidden_size)
        self.out = nn.Linear(hidden_size, output_size)

        self.attn = Attn(attn_model, hidden_size)

    def forward(self, input_step, last_hidden, encoder_outputs):
        # Note: we run this one step (word) at a time
        # Get embedding of current input word
        embedded = self.embedding(input_step)
        embedded = self.embedding_dropout(embedded)
        # Forward through unidirectional GRU
        rnn_output, hidden = self.gru(embedded, last_hidden)
        # Calculate attention weights from the current GRU output
        attn_weights = self.attn(rnn_output, encoder_outputs)
        # Multiply attention weights to encoder outputs to get new "weighted sum" context vector
        context = attn_weights.bmm(encoder_outputs.transpose(0, 1))
        # Concatenate weighted context vector and GRU output using Luong eq. 5
        rnn_output = rnn_output.squeeze(0)
        context = context.squeeze(1)
        concat_input = torch.cat((rnn_output, context), 1)
        concat_output = torch.tanh(self.concat(concat_input))
        # Predict next word using Luong eq. 6
        output = self.out(concat_output)
        output = F.softmax(output, dim=1)
        # Return output and final hidden state
        return output, hidden

Define Training Procedure

Masked loss

Since we are dealing with batches of padded sequences, we cannot simply consider all elements of the tensor when calculating loss. We define maskNLLLoss to calculate our loss based on our decoder’s output tensor, the target tensor, and a binary mask tensor describing the padding of the target tensor. This loss function calculates the average negative log likelihood of the elements that correspond to a 1 in the mask tensor.

def maskNLLLoss(inp, target, mask):
    nTotal = mask.sum()
    crossEntropy = -torch.log(torch.gather(inp, 1, target.view(-1, 1)).squeeze(1))
    loss = crossEntropy.masked_select(mask).mean()
    loss = loss.to(device)
    return loss, nTotal.item()

Single training iteration

The train function contains the algorithm for a single training iteration (a single batch of inputs).

We will use a couple of clever tricks to aid in convergence:

• The first trick is using teacher forcing. This means that at some probability, set by teacher_forcing_ratio, we use the current target word as the decoder’s next input rather than using the decoder’s current guess. This technique acts as training wheels for the decoder, aiding in more efficient training. However, teacher forcing can lead to model instability during inference, as the decoder may not have a sufficient chance to truly craft its own output sequences during training. Thus, we must be mindful of how we are setting the teacher_forcing_ratio, and not be fooled by fast convergence.

• The second trick that we implement is gradient clipping. This is a commonly used technique for countering the “exploding gradient” problem. In essence, by clipping or thresholding gradients to a maximum value, we prevent the gradients from growing exponentially and either overflow (NaN), or overshoot steep cliffs in the cost function.

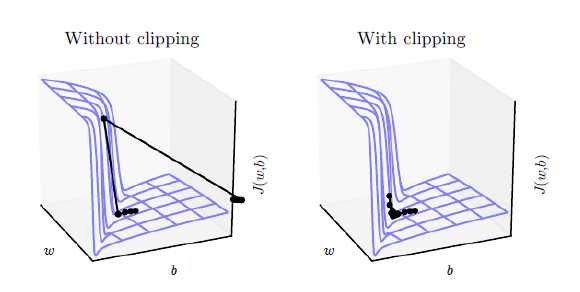
Image source: Goodfellow et al. Deep Learning. 2016. https://www.deeplearningbook.org/

Sequence of Operations:

1. Forward pass entire input batch through encoder.

2. Initialize decoder inputs as SOS_token, and hidden state as the encoder’s final hidden state.

3. Forward input batch sequence through decoder one time step at a time.

4. If teacher forcing: set next decoder input as the current target; else: set next decoder input as current decoder output.

5. Calculate and accumulate loss.

6. Perform backpropagation.

7. Clip gradients.

8. Update encoder and decoder model parameters.

Note

PyTorch’s RNN modules (RNN, LSTM, GRU) can be used like any other non-recurrent layers by simply passing them the entire input sequence (or batch of sequences). We use the GRU layer like this in the encoder. The reality is that under the hood, there is an iterative process looping over each time step calculating hidden states. Alternatively, you can run these modules one time-step at a time. In this case, we manually loop over the sequences during the training process like we must do for the decoder model. As long as you maintain the correct conceptual model of these modules, implementing sequential models can be very straightforward.

def train(input_variable, lengths, target_variable, mask, max_target_len, encoder, decoder, embedding,
          encoder_optimizer, decoder_optimizer, batch_size, clip, max_length=MAX_LENGTH):

    # Zero gradients
    encoder_optimizer.zero_grad()
    decoder_optimizer.zero_grad()

    # Set device options
    input_variable = input_variable.to(device)
    target_variable = target_variable.to(device)
    mask = mask.to(device)
    # Lengths for RNN packing should always be on the CPU
    lengths = lengths.to("cpu")

    # Initialize variables
    loss = 0
    print_losses = []
    n_totals = 0

    # Forward pass through encoder
    encoder_outputs, encoder_hidden = encoder(input_variable, lengths)

    # Create initial decoder input (start with SOS tokens for each sentence)
    decoder_input = torch.LongTensor([[SOS_token for _ in range(batch_size)]])
    decoder_input = decoder_input.to(device)

    # Set initial decoder hidden state to the encoder's final hidden state
    decoder_hidden = encoder_hidden[:decoder.n_layers]

    # Determine if we are using teacher forcing this iteration
    use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False

    # Forward batch of sequences through decoder one time step at a time
    if use_teacher_forcing:
        for t in range(max_target_len):
            decoder_output, decoder_hidden = decoder(
                decoder_input, decoder_hidden, encoder_outputs
            )
            # Teacher forcing: next input is current target
            decoder_input = target_variable[t].view(1, -1)
            # Calculate and accumulate loss
            mask_loss, nTotal = maskNLLLoss(decoder_output, target_variable[t], mask[t])
            loss += mask_loss
            print_losses.append(mask_loss.item() * nTotal)
            n_totals += nTotal
    else:
        for t in range(max_target_len):
            decoder_output, decoder_hidden = decoder(
                decoder_input, decoder_hidden, encoder_outputs
            )
            # No teacher forcing: next input is decoder's own current output
            _, topi = decoder_output.topk(1)
            decoder_input = torch.LongTensor([[topi[i][0] for i in range(batch_size)]])
            decoder_input = decoder_input.to(device)
            # Calculate and accumulate loss
            mask_loss, nTotal = maskNLLLoss(decoder_output, target_variable[t], mask[t])
            loss += mask_loss
            print_losses.append(mask_loss.item() * nTotal)
            n_totals += nTotal

    # Perform backpropagation
    loss.backward()

    # Clip gradients: gradients are modified in place
    _ = nn.utils.clip_grad_norm_(encoder.parameters(), clip)
    _ = nn.utils.clip_grad_norm_(decoder.parameters(), clip)

    # Adjust model weights
    encoder_optimizer.step()
    decoder_optimizer.step()

    return sum(print_losses) / n_totals

Training iterations

It is finally time to tie the full training procedure together with the data. The trainIters function is responsible for running n_iterations of training given the passed models, optimizers, data, etc. This function is quite self explanatory, as we have done the heavy lifting with the train function.

One thing to note is that when we save our model, we save a tarball containing the encoder and decoder state_dicts (parameters), the optimizers’ state_dicts, the loss, the iteration, etc. Saving the model in this way will give us the ultimate flexibility with the checkpoint. After loading a checkpoint, we will be able to use the model parameters to run inference, or we can continue training right where we left off.

def trainIters(model_name, voc, pairs, encoder, decoder, encoder_optimizer, decoder_optimizer, embedding, encoder_n_layers, decoder_n_layers, save_dir, n_iteration, batch_size, print_every, save_every, clip, corpus_name, loadFilename):

    # Load batches for each iteration
    training_batches = [batch2TrainData(voc, [random.choice(pairs) for _ in range(batch_size)])
                      for _ in range(n_iteration)]

    # Initializations
    print('Initializing ...')
    start_iteration = 1
    print_loss = 0
    if loadFilename:
        start_iteration = checkpoint['iteration'] + 1

    # Training loop
    print("Training...")
    for iteration in range(start_iteration, n_iteration + 1):
        training_batch = training_batches[iteration - 1]
        # Extract fields from batch
        input_variable, lengths, target_variable, mask, max_target_len = training_batch

        # Run a training iteration with batch
        loss = train(input_variable, lengths, target_variable, mask, max_target_len, encoder,
                     decoder, embedding, encoder_optimizer, decoder_optimizer, batch_size, clip)
        print_loss += loss

        # Print progress
        if iteration % print_every == 0:
            print_loss_avg = print_loss / print_every
            print("Iteration: {}; Percent complete: {:.1f}%; Average loss: {:.4f}".format(iteration, iteration / n_iteration * 100, print_loss_avg))
            print_loss = 0

        # Save checkpoint
        if (iteration % save_every == 0):
            directory = os.path.join(save_dir, model_name, corpus_name, '{}-{}_{}'.format(encoder_n_layers, decoder_n_layers, hidden_size))
            if not os.path.exists(directory):
                os.makedirs(directory)
            torch.save({
                'iteration': iteration,
                'en': encoder.state_dict(),
                'de': decoder.state_dict(),
                'en_opt': encoder_optimizer.state_dict(),
                'de_opt': decoder_optimizer.state_dict(),
                'loss': loss,
                'voc_dict': voc.__dict__,
                'embedding': embedding.state_dict()
            }, os.path.join(directory, '{}_{}.tar'.format(iteration, 'checkpoint')))

Define Evaluation

After training a model, we want to be able to talk to the bot ourselves. First, we must define how we want the model to decode the encoded input.

Greedy decoding

Greedy decoding is the decoding method that we use during training when we are NOT using teacher forcing. In other words, for each time step, we simply choose the word from decoder_output with the highest softmax value. This decoding method is optimal on a single time-step level.

To facilitate the greedy decoding operation, we define a GreedySearchDecoder class. When run, an object of this class takes an input sequence (input_seq) of shape (input_seq length, 1), a scalar input length (input_length) tensor, and a max_length to bound the response sentence length. The input sentence is evaluated using the following computational graph:

Computation Graph:

1. Forward input through encoder model.

2. Prepare encoder’s final hidden layer to be first hidden input to the decoder.

3. Initialize decoder’s first input as SOS_token.

4. Initialize tensors to append decoded words to.

5. Iteratively decode one word token at a time:

   1. Forward pass through decoder.

   2. Obtain most likely word token and its softmax score.

   3. Record token and score.

   4. Prepare current token to be next decoder input.

6. Return collections of word tokens and scores.

class GreedySearchDecoder(nn.Module):
    def __init__(self, encoder, decoder):
        super(GreedySearchDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, input_seq, input_length, max_length):
        # Forward input through encoder model
        encoder_outputs, encoder_hidden = self.encoder(input_seq, input_length)
        # Prepare encoder's final hidden layer to be first hidden input to the decoder
        decoder_hidden = encoder_hidden[:self.decoder.n_layers]
        # Initialize decoder input with SOS_token
        decoder_input = torch.ones(1, 1, device=device, dtype=torch.long) * SOS_token
        # Initialize tensors to append decoded words to
        all_tokens = torch.zeros([0], device=device, dtype=torch.long)
        all_scores = torch.zeros([0], device=device)
        # Iteratively decode one word token at a time
        for _ in range(max_length):
            # Forward pass through decoder
            decoder_output, decoder_hidden = self.decoder(decoder_input, decoder_hidden, encoder_outputs)
            # Obtain most likely word token and its softmax score
            decoder_scores, decoder_input = torch.max(decoder_output, dim=1)
            # Record token and score
            all_tokens = torch.cat((all_tokens, decoder_input), dim=0)
            all_scores = torch.cat((all_scores, decoder_scores), dim=0)
            # Prepare current token to be next decoder input (add a dimension)
            decoder_input = torch.unsqueeze(decoder_input, 0)
        # Return collections of word tokens and scores
        return all_tokens, all_scores

Evaluate my text

Now that we have our decoding method defined, we can write functions for evaluating a string input sentence. The evaluate function manages the low-level process of handling the input sentence. We first format the sentence as an input batch of word indexes with batch_size==1. We do this by converting the words of the sentence to their corresponding indexes, and transposing the dimensions to prepare the tensor for our models. We also create a lengths tensor which contains the length of our input sentence. In this case, lengths is scalar because we are only evaluating one sentence at a time (batch_size==1). Next, we obtain the decoded response sentence tensor using our GreedySearchDecoder object (searcher). Finally, we convert the response’s indexes to words and return the list of decoded words.

evaluateInput acts as the user interface for our chatbot. When called, an input text field will spawn in which we can enter our query sentence. After typing our input sentence and pressing Enter, our text is normalized in the same way as our training data, and is ultimately fed to the evaluate function to obtain a decoded output sentence. We loop this process, so we can keep chatting with our bot until we enter either “q” or “quit”.

Finally, if a sentence is entered that contains a word that is not in the vocabulary, we handle this gracefully by printing an error message and prompting the user to enter another sentence.

def evaluate(encoder, decoder, searcher, voc, sentence, max_length=MAX_LENGTH):
    ### Format input sentence as a batch
    # words -> indexes
    indexes_batch = [indexesFromSentence(voc, sentence)]
    # Create lengths tensor
    lengths = torch.tensor([len(indexes) for indexes in indexes_batch])
    # Transpose dimensions of batch to match models' expectations
    input_batch = torch.LongTensor(indexes_batch).transpose(0, 1)
    # Use appropriate device
    input_batch = input_batch.to(device)
    lengths = lengths.to("cpu")
    # Decode sentence with searcher
    tokens, scores = searcher(input_batch, lengths, max_length)
    # indexes -> words
    decoded_words = [voc.index2word[token.item()] for token in tokens]
    return decoded_words


def evaluateInput(encoder, decoder, searcher, voc):
    input_sentence = ''
    while(1):
        try:
            # Get input sentence
            input_sentence = input('> ')
            # Check if it is quit case
            if input_sentence == 'q' or input_sentence == 'quit': break
            # Normalize sentence
            input_sentence = normalizeString(input_sentence)
            # Evaluate sentence
            output_words = evaluate(encoder, decoder, searcher, voc, input_sentence)
            # Format and print response sentence
            output_words[:] = [x for x in output_words if not (x == 'EOS' or x == 'PAD')]
            print('Bot:', ' '.join(output_words))

        except KeyError:
            print("Error: Encountered unknown word.")

Run Model

Finally, it is time to run our model!

Regardless of whether we want to train or test the chatbot model, we must initialize the individual encoder and decoder models. In the following block, we set our desired configurations, choose to start from scratch or set a checkpoint to load from, and build and initialize the models. Feel free to play with different model configurations to optimize performance.

# Configure models
model_name = 'cb_model'
attn_model = 'dot'
#``attn_model = 'general'``
#``attn_model = 'concat'``
hidden_size = 500
encoder_n_layers = 2
decoder_n_layers = 2
dropout = 0.1
batch_size = 64

# Set checkpoint to load from; set to None if starting from scratch
loadFilename = None
checkpoint_iter = 4000

Sample code to load from a checkpoint:

loadFilename = os.path.join(save_dir, model_name, corpus_name,
                    '{}-{}_{}'.format(encoder_n_layers, decoder_n_layers, hidden_size),
                    '{}_checkpoint.tar'.format(checkpoint_iter))

# Load model if a ``loadFilename`` is provided
if loadFilename:
    # If loading on same machine the model was trained on
    checkpoint = torch.load(loadFilename)
    # If loading a model trained on GPU to CPU
    #checkpoint = torch.load(loadFilename, map_location=torch.device('cpu'))
    encoder_sd = checkpoint['en']
    decoder_sd = checkpoint['de']
    encoder_optimizer_sd = checkpoint['en_opt']
    decoder_optimizer_sd = checkpoint['de_opt']
    embedding_sd = checkpoint['embedding']
    voc.__dict__ = checkpoint['voc_dict']


print('Building encoder and decoder ...')
# Initialize word embeddings
embedding = nn.Embedding(voc.num_words, hidden_size)
if loadFilename:
    embedding.load_state_dict(embedding_sd)
# Initialize encoder & decoder models
encoder = EncoderRNN(hidden_size, embedding, encoder_n_layers, dropout)
decoder = LuongAttnDecoderRNN(attn_model, embedding, hidden_size, voc.num_words, decoder_n_layers, dropout)
if loadFilename:
    encoder.load_state_dict(encoder_sd)
    decoder.load_state_dict(decoder_sd)
# Use appropriate device
encoder = encoder.to(device)
decoder = decoder.to(device)
print('Models built and ready to go!')

Building encoder and decoder ...
Models built and ready to go!

Run Training

Run the following block if you want to train the model.

First we set training parameters, then we initialize our optimizers, and finally we call the trainIters function to run our training iterations.

# Configure training/optimization
clip = 50.0
teacher_forcing_ratio = 1.0
learning_rate = 0.0001
decoder_learning_ratio = 5.0
n_iteration = 4000
print_every = 1
save_every = 500

# Ensure dropout layers are in train mode
encoder.train()
decoder.train()

# Initialize optimizers
print('Building optimizers ...')
encoder_optimizer = optim.Adam(encoder.parameters(), lr=learning_rate)
decoder_optimizer = optim.Adam(decoder.parameters(), lr=learning_rate * decoder_learning_ratio)
if loadFilename:
    encoder_optimizer.load_state_dict(encoder_optimizer_sd)
    decoder_optimizer.load_state_dict(decoder_optimizer_sd)

# If you have an accelerator, configure it to call
for state in encoder_optimizer.state.values():
    for k, v in state.items():
        if isinstance(v, torch.Tensor):
            state[k] = v.to(device)

for state in decoder_optimizer.state.values():
    for k, v in state.items():
        if isinstance(v, torch.Tensor):
            state[k] = v.to(device)

# Run training iterations
print("Starting Training!")
trainIters(model_name, voc, pairs, encoder, decoder, encoder_optimizer, decoder_optimizer,
           embedding, encoder_n_layers, decoder_n_layers, save_dir, n_iteration, batch_size,
           print_every, save_every, clip, corpus_name, loadFilename)

Building optimizers ...
Starting Training!
Initializing ...
Training...
Iteration: 1; Percent complete: 0.0%; Average loss: 8.9593
Iteration: 2; Percent complete: 0.1%; Average loss: 8.8472
Iteration: 3; Percent complete: 0.1%; Average loss: 8.6653
Iteration: 4; Percent complete: 0.1%; Average loss: 8.4047
Iteration: 5; Percent complete: 0.1%; Average loss: 7.9620
Iteration: 6; Percent complete: 0.1%; Average loss: 7.3211
Iteration: 7; Percent complete: 0.2%; Average loss: 6.8639
Iteration: 8; Percent complete: 0.2%; Average loss: 6.7443
Iteration: 9; Percent complete: 0.2%; Average loss: 6.7959
Iteration: 10; Percent complete: 0.2%; Average loss: 6.6435
Iteration: 11; Percent complete: 0.3%; Average loss: 6.2495
Iteration: 12; Percent complete: 0.3%; Average loss: 5.8797
Iteration: 13; Percent complete: 0.3%; Average loss: 5.7192
Iteration: 14; Percent complete: 0.4%; Average loss: 5.4747
Iteration: 15; Percent complete: 0.4%; Average loss: 5.7640
Iteration: 16; Percent complete: 0.4%; Average loss: 5.5544
Iteration: 17; Percent complete: 0.4%; Average loss: 5.3071
Iteration: 18; Percent complete: 0.4%; Average loss: 5.2403
Iteration: 19; Percent complete: 0.5%; Average loss: 5.1796
Iteration: 20; Percent complete: 0.5%; Average loss: 5.0320
Iteration: 21; Percent complete: 0.5%; Average loss: 5.1562
Iteration: 22; Percent complete: 0.5%; Average loss: 4.8736
Iteration: 23; Percent complete: 0.6%; Average loss: 4.7804
Iteration: 24; Percent complete: 0.6%; Average loss: 4.8263
Iteration: 25; Percent complete: 0.6%; Average loss: 5.0634
Iteration: 26; Percent complete: 0.7%; Average loss: 4.8902
Iteration: 27; Percent complete: 0.7%; Average loss: 4.5832
Iteration: 28; Percent complete: 0.7%; Average loss: 4.7284
Iteration: 29; Percent complete: 0.7%; Average loss: 4.8047
Iteration: 30; Percent complete: 0.8%; Average loss: 4.7321
Iteration: 31; Percent complete: 0.8%; Average loss: 4.7071
Iteration: 32; Percent complete: 0.8%; Average loss: 4.7398
Iteration: 33; Percent complete: 0.8%; Average loss: 4.8656
Iteration: 34; Percent complete: 0.9%; Average loss: 4.6802
Iteration: 35; Percent complete: 0.9%; Average loss: 4.8539
Iteration: 36; Percent complete: 0.9%; Average loss: 5.1105
Iteration: 37; Percent complete: 0.9%; Average loss: 4.6751
Iteration: 38; Percent complete: 0.9%; Average loss: 4.7030
Iteration: 39; Percent complete: 1.0%; Average loss: 4.6700
Iteration: 40; Percent complete: 1.0%; Average loss: 5.0425
Iteration: 41; Percent complete: 1.0%; Average loss: 4.6704
Iteration: 42; Percent complete: 1.1%; Average loss: 4.8265
Iteration: 43; Percent complete: 1.1%; Average loss: 4.5477
Iteration: 44; Percent complete: 1.1%; Average loss: 4.6787
Iteration: 45; Percent complete: 1.1%; Average loss: 4.6418
Iteration: 46; Percent complete: 1.1%; Average loss: 4.6529
Iteration: 47; Percent complete: 1.2%; Average loss: 4.6123
Iteration: 48; Percent complete: 1.2%; Average loss: 4.6810
Iteration: 49; Percent complete: 1.2%; Average loss: 4.9625
Iteration: 50; Percent complete: 1.2%; Average loss: 4.6176
Iteration: 51; Percent complete: 1.3%; Average loss: 4.8487
Iteration: 52; Percent complete: 1.3%; Average loss: 4.5462
Iteration: 53; Percent complete: 1.3%; Average loss: 4.4331
Iteration: 54; Percent complete: 1.4%; Average loss: 4.7906
Iteration: 55; Percent complete: 1.4%; Average loss: 4.4676
Iteration: 56; Percent complete: 1.4%; Average loss: 4.4178
Iteration: 57; Percent complete: 1.4%; Average loss: 4.5971
Iteration: 58; Percent complete: 1.5%; Average loss: 4.5439
Iteration: 59; Percent complete: 1.5%; Average loss: 4.6777
Iteration: 60; Percent complete: 1.5%; Average loss: 4.4335
Iteration: 61; Percent complete: 1.5%; Average loss: 4.6212
Iteration: 62; Percent complete: 1.6%; Average loss: 4.6249
Iteration: 63; Percent complete: 1.6%; Average loss: 4.5420
Iteration: 64; Percent complete: 1.6%; Average loss: 4.7584
Iteration: 65; Percent complete: 1.6%; Average loss: 4.5151
Iteration: 66; Percent complete: 1.7%; Average loss: 4.4806
Iteration: 67; Percent complete: 1.7%; Average loss: 4.5057
Iteration: 68; Percent complete: 1.7%; Average loss: 4.5137
Iteration: 69; Percent complete: 1.7%; Average loss: 4.6782
Iteration: 70; Percent complete: 1.8%; Average loss: 4.4321
Iteration: 71; Percent complete: 1.8%; Average loss: 4.4393
Iteration: 72; Percent complete: 1.8%; Average loss: 4.4653
Iteration: 73; Percent complete: 1.8%; Average loss: 4.6589
Iteration: 74; Percent complete: 1.8%; Average loss: 4.5167
Iteration: 75; Percent complete: 1.9%; Average loss: 4.5851
Iteration: 76; Percent complete: 1.9%; Average loss: 4.5281
Iteration: 77; Percent complete: 1.9%; Average loss: 4.5567
Iteration: 78; Percent complete: 1.9%; Average loss: 4.5989
Iteration: 79; Percent complete: 2.0%; Average loss: 4.4800
Iteration: 80; Percent complete: 2.0%; Average loss: 4.6004
Iteration: 81; Percent complete: 2.0%; Average loss: 4.6403
Iteration: 82; Percent complete: 2.1%; Average loss: 4.3536
Iteration: 83; Percent complete: 2.1%; Average loss: 4.6622
Iteration: 84; Percent complete: 2.1%; Average loss: 4.3472
Iteration: 85; Percent complete: 2.1%; Average loss: 4.6298
Iteration: 86; Percent complete: 2.1%; Average loss: 4.5869
Iteration: 87; Percent complete: 2.2%; Average loss: 4.5427
Iteration: 88; Percent complete: 2.2%; Average loss: 4.6469
Iteration: 89; Percent complete: 2.2%; Average loss: 4.5998
Iteration: 90; Percent complete: 2.2%; Average loss: 4.4985
Iteration: 91; Percent complete: 2.3%; Average loss: 4.4448
Iteration: 92; Percent complete: 2.3%; Average loss: 4.5478
Iteration: 93; Percent complete: 2.3%; Average loss: 4.4148
Iteration: 94; Percent complete: 2.4%; Average loss: 4.7306
Iteration: 95; Percent complete: 2.4%; Average loss: 4.5339
Iteration: 96; Percent complete: 2.4%; Average loss: 4.5407
Iteration: 97; Percent complete: 2.4%; Average loss: 4.6130
Iteration: 98; Percent complete: 2.5%; Average loss: 4.5783
Iteration: 99; Percent complete: 2.5%; Average loss: 4.3342
Iteration: 100; Percent complete: 2.5%; Average loss: 4.5073
Iteration: 101; Percent complete: 2.5%; Average loss: 4.5573
Iteration: 102; Percent complete: 2.5%; Average loss: 4.4550
Iteration: 103; Percent complete: 2.6%; Average loss: 4.4272
Iteration: 104; Percent complete: 2.6%; Average loss: 4.4306
Iteration: 105; Percent complete: 2.6%; Average loss: 4.3232
Iteration: 106; Percent complete: 2.6%; Average loss: 4.5353
Iteration: 107; Percent complete: 2.7%; Average loss: 4.2801
Iteration: 108; Percent complete: 2.7%; Average loss: 4.2249
Iteration: 109; Percent complete: 2.7%; Average loss: 4.1911
Iteration: 110; Percent complete: 2.8%; Average loss: 4.3876
Iteration: 111; Percent complete: 2.8%; Average loss: 4.3892
Iteration: 112; Percent complete: 2.8%; Average loss: 4.3454
Iteration: 113; Percent complete: 2.8%; Average loss: 4.2302
Iteration: 114; Percent complete: 2.9%; Average loss: 4.4349
Iteration: 115; Percent complete: 2.9%; Average loss: 4.3253
Iteration: 116; Percent complete: 2.9%; Average loss: 4.3720
Iteration: 117; Percent complete: 2.9%; Average loss: 4.4408
Iteration: 118; Percent complete: 2.9%; Average loss: 4.2546
Iteration: 119; Percent complete: 3.0%; Average loss: 4.2743
Iteration: 120; Percent complete: 3.0%; Average loss: 4.4487
Iteration: 121; Percent complete: 3.0%; Average loss: 4.6132
Iteration: 122; Percent complete: 3.0%; Average loss: 4.2870
Iteration: 123; Percent complete: 3.1%; Average loss: 4.6049
Iteration: 124; Percent complete: 3.1%; Average loss: 4.2827
Iteration: 125; Percent complete: 3.1%; Average loss: 4.1421
Iteration: 126; Percent complete: 3.1%; Average loss: 4.1383
Iteration: 127; Percent complete: 3.2%; Average loss: 4.3451
Iteration: 128; Percent complete: 3.2%; Average loss: 4.3673
Iteration: 129; Percent complete: 3.2%; Average loss: 4.1818
Iteration: 130; Percent complete: 3.2%; Average loss: 4.3564
Iteration: 131; Percent complete: 3.3%; Average loss: 4.2683
Iteration: 132; Percent complete: 3.3%; Average loss: 4.4326
Iteration: 133; Percent complete: 3.3%; Average loss: 4.4287
Iteration: 134; Percent complete: 3.4%; Average loss: 4.2107
Iteration: 135; Percent complete: 3.4%; Average loss: 4.3633
Iteration: 136; Percent complete: 3.4%; Average loss: 4.4046
Iteration: 137; Percent complete: 3.4%; Average loss: 4.0548
Iteration: 138; Percent complete: 3.5%; Average loss: 4.3662
Iteration: 139; Percent complete: 3.5%; Average loss: 4.1950
Iteration: 140; Percent complete: 3.5%; Average loss: 4.2784
Iteration: 141; Percent complete: 3.5%; Average loss: 4.2290
Iteration: 142; Percent complete: 3.5%; Average loss: 4.2270
Iteration: 143; Percent complete: 3.6%; Average loss: 3.9679
Iteration: 144; Percent complete: 3.6%; Average loss: 4.1348
Iteration: 145; Percent complete: 3.6%; Average loss: 4.4784
Iteration: 146; Percent complete: 3.6%; Average loss: 4.4069
Iteration: 147; Percent complete: 3.7%; Average loss: 4.3790
Iteration: 148; Percent complete: 3.7%; Average loss: 3.9888
Iteration: 149; Percent complete: 3.7%; Average loss: 4.1557
Iteration: 150; Percent complete: 3.8%; Average loss: 4.3400
Iteration: 151; Percent complete: 3.8%; Average loss: 4.3081
Iteration: 152; Percent complete: 3.8%; Average loss: 4.5631
Iteration: 153; Percent complete: 3.8%; Average loss: 4.1315
Iteration: 154; Percent complete: 3.9%; Average loss: 4.0034
Iteration: 155; Percent complete: 3.9%; Average loss: 4.2004
Iteration: 156; Percent complete: 3.9%; Average loss: 4.3940
Iteration: 157; Percent complete: 3.9%; Average loss: 4.2039
Iteration: 158; Percent complete: 4.0%; Average loss: 4.1580
Iteration: 159; Percent complete: 4.0%; Average loss: 4.3536
Iteration: 160; Percent complete: 4.0%; Average loss: 4.4848
Iteration: 161; Percent complete: 4.0%; Average loss: 4.1957
Iteration: 162; Percent complete: 4.0%; Average loss: 4.3004
Iteration: 163; Percent complete: 4.1%; Average loss: 4.1515
Iteration: 164; Percent complete: 4.1%; Average loss: 4.1793
Iteration: 165; Percent complete: 4.1%; Average loss: 4.1029
Iteration: 166; Percent complete: 4.2%; Average loss: 3.9772
Iteration: 167; Percent complete: 4.2%; Average loss: 4.5324
Iteration: 168; Percent complete: 4.2%; Average loss: 3.9004
Iteration: 169; Percent complete: 4.2%; Average loss: 4.1583
Iteration: 170; Percent complete: 4.2%; Average loss: 4.3400
Iteration: 171; Percent complete: 4.3%; Average loss: 3.9570
Iteration: 172; Percent complete: 4.3%; Average loss: 4.0705
Iteration: 173; Percent complete: 4.3%; Average loss: 4.1178
Iteration: 174; Percent complete: 4.3%; Average loss: 4.0946
Iteration: 175; Percent complete: 4.4%; Average loss: 4.3531
Iteration: 176; Percent complete: 4.4%; Average loss: 4.1943
Iteration: 177; Percent complete: 4.4%; Average loss: 4.0386
Iteration: 178; Percent complete: 4.5%; Average loss: 4.1303
Iteration: 179; Percent complete: 4.5%; Average loss: 4.1000
Iteration: 180; Percent complete: 4.5%; Average loss: 4.3553
Iteration: 181; Percent complete: 4.5%; Average loss: 4.1854
Iteration: 182; Percent complete: 4.5%; Average loss: 4.2616
Iteration: 183; Percent complete: 4.6%; Average loss: 4.1199
Iteration: 184; Percent complete: 4.6%; Average loss: 4.1040
Iteration: 185; Percent complete: 4.6%; Average loss: 3.9708
Iteration: 186; Percent complete: 4.7%; Average loss: 4.3033
Iteration: 187; Percent complete: 4.7%; Average loss: 4.3823
Iteration: 188; Percent complete: 4.7%; Average loss: 4.4481
Iteration: 189; Percent complete: 4.7%; Average loss: 4.1277
Iteration: 190; Percent complete: 4.8%; Average loss: 4.1850
Iteration: 191; Percent complete: 4.8%; Average loss: 4.2930
Iteration: 192; Percent complete: 4.8%; Average loss: 4.2519
Iteration: 193; Percent complete: 4.8%; Average loss: 4.0494
Iteration: 194; Percent complete: 4.9%; Average loss: 4.0533
Iteration: 195; Percent complete: 4.9%; Average loss: 4.2194
Iteration: 196; Percent complete: 4.9%; Average loss: 4.0419
Iteration: 197; Percent complete: 4.9%; Average loss: 3.8985
Iteration: 198; Percent complete: 5.0%; Average loss: 4.3023
Iteration: 199; Percent complete: 5.0%; Average loss: 4.1445
Iteration: 200; Percent complete: 5.0%; Average loss: 4.1074
Iteration: 201; Percent complete: 5.0%; Average loss: 4.2756
Iteration: 202; Percent complete: 5.1%; Average loss: 4.1767
Iteration: 203; Percent complete: 5.1%; Average loss: 4.1922
Iteration: 204; Percent complete: 5.1%; Average loss: 3.9076
Iteration: 205; Percent complete: 5.1%; Average loss: 4.2431
Iteration: 206; Percent complete: 5.1%; Average loss: 3.9489
Iteration: 207; Percent complete: 5.2%; Average loss: 4.3070
Iteration: 208; Percent complete: 5.2%; Average loss: 3.9109
Iteration: 209; Percent complete: 5.2%; Average loss: 3.8726
Iteration: 210; Percent complete: 5.2%; Average loss: 4.0917
Iteration: 211; Percent complete: 5.3%; Average loss: 4.2007
Iteration: 212; Percent complete: 5.3%; Average loss: 4.2044
Iteration: 213; Percent complete: 5.3%; Average loss: 4.1330
Iteration: 214; Percent complete: 5.3%; Average loss: 4.2194
Iteration: 215; Percent complete: 5.4%; Average loss: 3.8391
Iteration: 216; Percent complete: 5.4%; Average loss: 4.1030
Iteration: 217; Percent complete: 5.4%; Average loss: 3.9809
Iteration: 218; Percent complete: 5.5%; Average loss: 4.0140
Iteration: 219; Percent complete: 5.5%; Average loss: 4.0752
Iteration: 220; Percent complete: 5.5%; Average loss: 4.0725
Iteration: 221; Percent complete: 5.5%; Average loss: 4.2150
Iteration: 222; Percent complete: 5.5%; Average loss: 3.8631
Iteration: 223; Percent complete: 5.6%; Average loss: 3.9445
Iteration: 224; Percent complete: 5.6%; Average loss: 4.2058
Iteration: 225; Percent complete: 5.6%; Average loss: 4.1089
Iteration: 226; Percent complete: 5.7%; Average loss: 4.0165
Iteration: 227; Percent complete: 5.7%; Average loss: 3.7707
Iteration: 228; Percent complete: 5.7%; Average loss: 3.8709
Iteration: 229; Percent complete: 5.7%; Average loss: 3.9952
Iteration: 230; Percent complete: 5.8%; Average loss: 4.1963
Iteration: 231; Percent complete: 5.8%; Average loss: 4.1791
Iteration: 232; Percent complete: 5.8%; Average loss: 4.1398
Iteration: 233; Percent complete: 5.8%; Average loss: 4.1461
Iteration: 234; Percent complete: 5.9%; Average loss: 4.0053
Iteration: 235; Percent complete: 5.9%; Average loss: 4.2647
Iteration: 236; Percent complete: 5.9%; Average loss: 3.9447
Iteration: 237; Percent complete: 5.9%; Average loss: 3.8255
Iteration: 238; Percent complete: 5.9%; Average loss: 4.2394
Iteration: 239; Percent complete: 6.0%; Average loss: 3.8456
Iteration: 240; Percent complete: 6.0%; Average loss: 4.0987
Iteration: 241; Percent complete: 6.0%; Average loss: 4.2535
Iteration: 242; Percent complete: 6.0%; Average loss: 3.9507
Iteration: 243; Percent complete: 6.1%; Average loss: 4.1112
Iteration: 244; Percent complete: 6.1%; Average loss: 3.9541
Iteration: 245; Percent complete: 6.1%; Average loss: 3.9355
Iteration: 246; Percent complete: 6.2%; Average loss: 4.0023
Iteration: 247; Percent complete: 6.2%; Average loss: 4.1820
Iteration: 248; Percent complete: 6.2%; Average loss: 3.8539
Iteration: 249; Percent complete: 6.2%; Average loss: 3.8043
Iteration: 250; Percent complete: 6.2%; Average loss: 3.9720
Iteration: 251; Percent complete: 6.3%; Average loss: 4.3986
Iteration: 252; Percent complete: 6.3%; Average loss: 3.8389
Iteration: 253; Percent complete: 6.3%; Average loss: 3.9434
Iteration: 254; Percent complete: 6.3%; Average loss: 3.7063
Iteration: 255; Percent complete: 6.4%; Average loss: 3.9748
Iteration: 256; Percent complete: 6.4%; Average loss: 3.8536
Iteration: 257; Percent complete: 6.4%; Average loss: 4.1303
Iteration: 258; Percent complete: 6.5%; Average loss: 4.0024
Iteration: 259; Percent complete: 6.5%; Average loss: 3.9873
Iteration: 260; Percent complete: 6.5%; Average loss: 3.8084
Iteration: 261; Percent complete: 6.5%; Average loss: 4.0853
Iteration: 262; Percent complete: 6.6%; Average loss: 3.8095
Iteration: 263; Percent complete: 6.6%; Average loss: 4.0856
Iteration: 264; Percent complete: 6.6%; Average loss: 3.8345
Iteration: 265; Percent complete: 6.6%; Average loss: 3.8303
Iteration: 266; Percent complete: 6.7%; Average loss: 4.1457
Iteration: 267; Percent complete: 6.7%; Average loss: 3.6852
Iteration: 268; Percent complete: 6.7%; Average loss: 3.7948
Iteration: 269; Percent complete: 6.7%; Average loss: 4.1753
Iteration: 270; Percent complete: 6.8%; Average loss: 3.9155
Iteration: 271; Percent complete: 6.8%; Average loss: 3.7520
Iteration: 272; Percent complete: 6.8%; Average loss: 3.9056
Iteration: 273; Percent complete: 6.8%; Average loss: 3.8919
Iteration: 274; Percent complete: 6.9%; Average loss: 4.0330
Iteration: 275; Percent complete: 6.9%; Average loss: 4.1079
Iteration: 276; Percent complete: 6.9%; Average loss: 4.0373
Iteration: 277; Percent complete: 6.9%; Average loss: 3.9118
Iteration: 278; Percent complete: 7.0%; Average loss: 4.1698
Iteration: 279; Percent complete: 7.0%; Average loss: 3.8019
Iteration: 280; Percent complete: 7.0%; Average loss: 4.0669
Iteration: 281; Percent complete: 7.0%; Average loss: 3.7545
Iteration: 282; Percent complete: 7.0%; Average loss: 4.0579
Iteration: 283; Percent complete: 7.1%; Average loss: 3.9881
Iteration: 284; Percent complete: 7.1%; Average loss: 3.8612
Iteration: 285; Percent complete: 7.1%; Average loss: 3.8630
Iteration: 286; Percent complete: 7.1%; Average loss: 4.1072
Iteration: 287; Percent complete: 7.2%; Average loss: 4.0799
Iteration: 288; Percent complete: 7.2%; Average loss: 4.2736
Iteration: 289; Percent complete: 7.2%; Average loss: 3.7678
Iteration: 290; Percent complete: 7.2%; Average loss: 3.8528
Iteration: 291; Percent complete: 7.3%; Average loss: 3.9492
Iteration: 292; Percent complete: 7.3%; Average loss: 4.1858
Iteration: 293; Percent complete: 7.3%; Average loss: 3.8409
Iteration: 294; Percent complete: 7.3%; Average loss: 4.1362
Iteration: 295; Percent complete: 7.4%; Average loss: 4.0525
Iteration: 296; Percent complete: 7.4%; Average loss: 3.8770
Iteration: 297; Percent complete: 7.4%; Average loss: 3.7530
Iteration: 298; Percent complete: 7.4%; Average loss: 4.0661
Iteration: 299; Percent complete: 7.5%; Average loss: 3.7899
Iteration: 300; Percent complete: 7.5%; Average loss: 4.2544
Iteration: 301; Percent complete: 7.5%; Average loss: 3.9104
Iteration: 302; Percent complete: 7.5%; Average loss: 3.7920
Iteration: 303; Percent complete: 7.6%; Average loss: 4.1264
Iteration: 304; Percent complete: 7.6%; Average loss: 3.9854
Iteration: 305; Percent complete: 7.6%; Average loss: 3.9249
Iteration: 306; Percent complete: 7.6%; Average loss: 3.6512
Iteration: 307; Percent complete: 7.7%; Average loss: 4.0736
Iteration: 308; Percent complete: 7.7%; Average loss: 3.8574
Iteration: 309; Percent complete: 7.7%; Average loss: 3.7592
Iteration: 310; Percent complete: 7.8%; Average loss: 4.1177
Iteration: 311; Percent complete: 7.8%; Average loss: 3.9124
Iteration: 312; Percent complete: 7.8%; Average loss: 3.9536
Iteration: 313; Percent complete: 7.8%; Average loss: 3.8323
Iteration: 314; Percent complete: 7.8%; Average loss: 3.9195
Iteration: 315; Percent complete: 7.9%; Average loss: 3.9315
Iteration: 316; Percent complete: 7.9%; Average loss: 4.0970
Iteration: 317; Percent complete: 7.9%; Average loss: 4.1048
Iteration: 318; Percent complete: 8.0%; Average loss: 4.1663
Iteration: 319; Percent complete: 8.0%; Average loss: 3.7576
Iteration: 320; Percent complete: 8.0%; Average loss: 3.7679
Iteration: 321; Percent complete: 8.0%; Average loss: 3.6503
Iteration: 322; Percent complete: 8.1%; Average loss: 4.1565
Iteration: 323; Percent complete: 8.1%; Average loss: 3.8728
Iteration: 324; Percent complete: 8.1%; Average loss: 4.0254
Iteration: 325; Percent complete: 8.1%; Average loss: 3.6823
Iteration: 326; Percent complete: 8.2%; Average loss: 3.8821
Iteration: 327; Percent complete: 8.2%; Average loss: 3.9548
Iteration: 328; Percent complete: 8.2%; Average loss: 4.0258
Iteration: 329; Percent complete: 8.2%; Average loss: 3.9607
Iteration: 330; Percent complete: 8.2%; Average loss: 3.9788
Iteration: 331; Percent complete: 8.3%; Average loss: 4.1168
Iteration: 332; Percent complete: 8.3%; Average loss: 3.5741
Iteration: 333; Percent complete: 8.3%; Average loss: 3.8899
Iteration: 334; Percent complete: 8.3%; Average loss: 3.8563
Iteration: 335; Percent complete: 8.4%; Average loss: 4.2089
Iteration: 336; Percent complete: 8.4%; Average loss: 3.9633
Iteration: 337; Percent complete: 8.4%; Average loss: 3.8235
Iteration: 338; Percent complete: 8.5%; Average loss: 3.8286
Iteration: 339; Percent complete: 8.5%; Average loss: 3.8186
Iteration: 340; Percent complete: 8.5%; Average loss: 3.8443
Iteration: 341; Percent complete: 8.5%; Average loss: 3.8430
Iteration: 342; Percent complete: 8.6%; Average loss: 3.8205
Iteration: 343; Percent complete: 8.6%; Average loss: 4.0368
Iteration: 344; Percent complete: 8.6%; Average loss: 3.9795
Iteration: 345; Percent complete: 8.6%; Average loss: 3.8423
Iteration: 346; Percent complete: 8.6%; Average loss: 4.1615
Iteration: 347; Percent complete: 8.7%; Average loss: 3.8655
Iteration: 348; Percent complete: 8.7%; Average loss: 4.0717
Iteration: 349; Percent complete: 8.7%; Average loss: 3.9484
Iteration: 350; Percent complete: 8.8%; Average loss: 3.8271
Iteration: 351; Percent complete: 8.8%; Average loss: 3.7187
Iteration: 352; Percent complete: 8.8%; Average loss: 3.8340
Iteration: 353; Percent complete: 8.8%; Average loss: 3.9542
Iteration: 354; Percent complete: 8.8%; Average loss: 3.6857
Iteration: 355; Percent complete: 8.9%; Average loss: 3.5153
Iteration: 356; Percent complete: 8.9%; Average loss: 4.0032
Iteration: 357; Percent complete: 8.9%; Average loss: 3.7836
Iteration: 358; Percent complete: 8.9%; Average loss: 3.7636
Iteration: 359; Percent complete: 9.0%; Average loss: 3.8494
Iteration: 360; Percent complete: 9.0%; Average loss: 3.7220
Iteration: 361; Percent complete: 9.0%; Average loss: 3.8158
Iteration: 362; Percent complete: 9.0%; Average loss: 3.9703
Iteration: 363; Percent complete: 9.1%; Average loss: 3.7899
Iteration: 364; Percent complete: 9.1%; Average loss: 3.7184
Iteration: 365; Percent complete: 9.1%; Average loss: 3.9077
Iteration: 366; Percent complete: 9.2%; Average loss: 3.7486
Iteration: 367; Percent complete: 9.2%; Average loss: 3.8215
Iteration: 368; Percent complete: 9.2%; Average loss: 3.8328
Iteration: 369; Percent complete: 9.2%; Average loss: 3.9024
Iteration: 370; Percent complete: 9.2%; Average loss: 3.8267
Iteration: 371; Percent complete: 9.3%; Average loss: 4.2183
Iteration: 372; Percent complete: 9.3%; Average loss: 3.9856
Iteration: 373; Percent complete: 9.3%; Average loss: 4.0821
Iteration: 374; Percent complete: 9.3%; Average loss: 4.0290
Iteration: 375; Percent complete: 9.4%; Average loss: 3.8477
Iteration: 376; Percent complete: 9.4%; Average loss: 3.9600
Iteration: 377; Percent complete: 9.4%; Average loss: 3.8235
Iteration: 378; Percent complete: 9.4%; Average loss: 4.0711
Iteration: 379; Percent complete: 9.5%; Average loss: 3.7405
Iteration: 380; Percent complete: 9.5%; Average loss: 3.6503
Iteration: 381; Percent complete: 9.5%; Average loss: 3.7631
Iteration: 382; Percent complete: 9.6%; Average loss: 3.7343
Iteration: 383; Percent complete: 9.6%; Average loss: 3.7362
Iteration: 384; Percent complete: 9.6%; Average loss: 3.7828
Iteration: 385; Percent complete: 9.6%; Average loss: 3.8998
Iteration: 386; Percent complete: 9.7%; Average loss: 3.6771
Iteration: 387; Percent complete: 9.7%; Average loss: 3.9335
Iteration: 388; Percent complete: 9.7%; Average loss: 3.9583
Iteration: 389; Percent complete: 9.7%; Average loss: 3.8574
Iteration: 390; Percent complete: 9.8%; Average loss: 3.6371
Iteration: 391; Percent complete: 9.8%; Average loss: 3.6817
Iteration: 392; Percent complete: 9.8%; Average loss: 4.0134
Iteration: 393; Percent complete: 9.8%; Average loss: 4.0628
Iteration: 394; Percent complete: 9.8%; Average loss: 3.8610
Iteration: 395; Percent complete: 9.9%; Average loss: 3.8071
Iteration: 396; Percent complete: 9.9%; Average loss: 4.1399
Iteration: 397; Percent complete: 9.9%; Average loss: 3.8319
Iteration: 398; Percent complete: 10.0%; Average loss: 3.7781
Iteration: 399; Percent complete: 10.0%; Average loss: 3.7585
Iteration: 400; Percent complete: 10.0%; Average loss: 3.7145
Iteration: 401; Percent complete: 10.0%; Average loss: 3.6450
Iteration: 402; Percent complete: 10.1%; Average loss: 4.0713
Iteration: 403; Percent complete: 10.1%; Average loss: 3.5382
Iteration: 404; Percent complete: 10.1%; Average loss: 3.6763
Iteration: 405; Percent complete: 10.1%; Average loss: 3.7159
Iteration: 406; Percent complete: 10.2%; Average loss: 3.7218
Iteration: 407; Percent complete: 10.2%; Average loss: 3.8507
Iteration: 408; Percent complete: 10.2%; Average loss: 4.0023
Iteration: 409; Percent complete: 10.2%; Average loss: 3.7232
Iteration: 410; Percent complete: 10.2%; Average loss: 4.0149
Iteration: 411; Percent complete: 10.3%; Average loss: 3.9551
Iteration: 412; Percent complete: 10.3%; Average loss: 3.9125
Iteration: 413; Percent complete: 10.3%; Average loss: 4.0622
Iteration: 414; Percent complete: 10.3%; Average loss: 3.8236
Iteration: 415; Percent complete: 10.4%; Average loss: 3.7414
Iteration: 416; Percent complete: 10.4%; Average loss: 3.9144
Iteration: 417; Percent complete: 10.4%; Average loss: 3.7852
Iteration: 418; Percent complete: 10.4%; Average loss: 3.9505
Iteration: 419; Percent complete: 10.5%; Average loss: 4.0037
Iteration: 420; Percent complete: 10.5%; Average loss: 3.8543
Iteration: 421; Percent complete: 10.5%; Average loss: 3.6483
Iteration: 422; Percent complete: 10.5%; Average loss: 3.8967
Iteration: 423; Percent complete: 10.6%; Average loss: 3.7419
Iteration: 424; Percent complete: 10.6%; Average loss: 3.9552
Iteration: 425; Percent complete: 10.6%; Average loss: 3.9251
Iteration: 426; Percent complete: 10.7%; Average loss: 3.8727
Iteration: 427; Percent complete: 10.7%; Average loss: 3.7482
Iteration: 428; Percent complete: 10.7%; Average loss: 3.7193
Iteration: 429; Percent complete: 10.7%; Average loss: 3.7143
Iteration: 430; Percent complete: 10.8%; Average loss: 3.9710
Iteration: 431; Percent complete: 10.8%; Average loss: 3.6732
Iteration: 432; Percent complete: 10.8%; Average loss: 3.6823
Iteration: 433; Percent complete: 10.8%; Average loss: 3.6733
Iteration: 434; Percent complete: 10.8%; Average loss: 3.8525
Iteration: 435; Percent complete: 10.9%; Average loss: 3.7475
Iteration: 436; Percent complete: 10.9%; Average loss: 3.6755
Iteration: 437; Percent complete: 10.9%; Average loss: 3.6399
Iteration: 438; Percent complete: 10.9%; Average loss: 3.8141
Iteration: 439; Percent complete: 11.0%; Average loss: 3.9201
Iteration: 440; Percent complete: 11.0%; Average loss: 3.6257
Iteration: 441; Percent complete: 11.0%; Average loss: 4.0331
Iteration: 442; Percent complete: 11.1%; Average loss: 4.0121
Iteration: 443; Percent complete: 11.1%; Average loss: 3.7036
Iteration: 444; Percent complete: 11.1%; Average loss: 4.0100
Iteration: 445; Percent complete: 11.1%; Average loss: 3.6350
Iteration: 446; Percent complete: 11.2%; Average loss: 4.0496
Iteration: 447; Percent complete: 11.2%; Average loss: 3.9086
Iteration: 448; Percent complete: 11.2%; Average loss: 3.8360
Iteration: 449; Percent complete: 11.2%; Average loss: 3.8767
Iteration: 450; Percent complete: 11.2%; Average loss: 3.6600
Iteration: 451; Percent complete: 11.3%; Average loss: 3.5081
Iteration: 452; Percent complete: 11.3%; Average loss: 3.5347
Iteration: 453; Percent complete: 11.3%; Average loss: 3.5127
Iteration: 454; Percent complete: 11.3%; Average loss: 3.6288
Iteration: 455; Percent complete: 11.4%; Average loss: 3.8699
Iteration: 456; Percent complete: 11.4%; Average loss: 3.6518
Iteration: 457; Percent complete: 11.4%; Average loss: 4.1302
Iteration: 458; Percent complete: 11.5%; Average loss: 3.5999
Iteration: 459; Percent complete: 11.5%; Average loss: 3.9544
Iteration: 460; Percent complete: 11.5%; Average loss: 3.9086
Iteration: 461; Percent complete: 11.5%; Average loss: 3.9633
Iteration: 462; Percent complete: 11.6%; Average loss: 3.5339
Iteration: 463; Percent complete: 11.6%; Average loss: 3.7288
Iteration: 464; Percent complete: 11.6%; Average loss: 3.7750
Iteration: 465; Percent complete: 11.6%; Average loss: 3.6061
Iteration: 466; Percent complete: 11.7%; Average loss: 4.1877
Iteration: 467; Percent complete: 11.7%; Average loss: 3.9388
Iteration: 468; Percent complete: 11.7%; Average loss: 3.8212
Iteration: 469; Percent complete: 11.7%; Average loss: 3.6989
Iteration: 470; Percent complete: 11.8%; Average loss: 3.5593
Iteration: 471; Percent complete: 11.8%; Average loss: 3.5784
Iteration: 472; Percent complete: 11.8%; Average loss: 3.7153
Iteration: 473; Percent complete: 11.8%; Average loss: 3.6385
Iteration: 474; Percent complete: 11.8%; Average loss: 3.8274
Iteration: 475; Percent complete: 11.9%; Average loss: 3.5783
Iteration: 476; Percent complete: 11.9%; Average loss: 3.6519
Iteration: 477; Percent complete: 11.9%; Average loss: 3.8041
Iteration: 478; Percent complete: 11.9%; Average loss: 3.7013
Iteration: 479; Percent complete: 12.0%; Average loss: 3.5652
Iteration: 480; Percent complete: 12.0%; Average loss: 3.8202
Iteration: 481; Percent complete: 12.0%; Average loss: 3.7590
Iteration: 482; Percent complete: 12.0%; Average loss: 3.6681
Iteration: 483; Percent complete: 12.1%; Average loss: 3.6569
Iteration: 484; Percent complete: 12.1%; Average loss: 3.6522
Iteration: 485; Percent complete: 12.1%; Average loss: 3.6967
Iteration: 486; Percent complete: 12.2%; Average loss: 3.7874
Iteration: 487; Percent complete: 12.2%; Average loss: 3.7049
Iteration: 488; Percent complete: 12.2%; Average loss: 3.9728
Iteration: 489; Percent complete: 12.2%; Average loss: 3.8207
Iteration: 490; Percent complete: 12.2%; Average loss: 3.7917
Iteration: 491; Percent complete: 12.3%; Average loss: 3.7360
Iteration: 492; Percent complete: 12.3%; Average loss: 3.7364
Iteration: 493; Percent complete: 12.3%; Average loss: 3.4418
Iteration: 494; Percent complete: 12.3%; Average loss: 3.5935
Iteration: 495; Percent complete: 12.4%; Average loss: 3.6265
Iteration: 496; Percent complete: 12.4%; Average loss: 3.8493
Iteration: 497; Percent complete: 12.4%; Average loss: 3.2536
Iteration: 498; Percent complete: 12.4%; Average loss: 3.5935
Iteration: 499; Percent complete: 12.5%; Average loss: 3.9840
Iteration: 500; Percent complete: 12.5%; Average loss: 3.8465
Iteration: 501; Percent complete: 12.5%; Average loss: 3.6511
Iteration: 502; Percent complete: 12.6%; Average loss: 3.6601
Iteration: 503; Percent complete: 12.6%; Average loss: 3.7214
Iteration: 504; Percent complete: 12.6%; Average loss: 3.6963
Iteration: 505; Percent complete: 12.6%; Average loss: 3.8245
Iteration: 506; Percent complete: 12.7%; Average loss: 3.6235
Iteration: 507; Percent complete: 12.7%; Average loss: 3.5950
Iteration: 508; Percent complete: 12.7%; Average loss: 3.7619
Iteration: 509; Percent complete: 12.7%; Average loss: 3.8069
Iteration: 510; Percent complete: 12.8%; Average loss: 3.6812
Iteration: 511; Percent complete: 12.8%; Average loss: 3.5033
Iteration: 512; Percent complete: 12.8%; Average loss: 3.5128
Iteration: 513; Percent complete: 12.8%; Average loss: 3.8524
Iteration: 514; Percent complete: 12.8%; Average loss: 3.8338
Iteration: 515; Percent complete: 12.9%; Average loss: 3.6048
Iteration: 516; Percent complete: 12.9%; Average loss: 3.8825
Iteration: 517; Percent complete: 12.9%; Average loss: 3.6929
Iteration: 518; Percent complete: 13.0%; Average loss: 3.9309
Iteration: 519; Percent complete: 13.0%; Average loss: 3.8239
Iteration: 520; Percent complete: 13.0%; Average loss: 3.6996
Iteration: 521; Percent complete: 13.0%; Average loss: 3.7923
Iteration: 522; Percent complete: 13.1%; Average loss: 3.8344
Iteration: 523; Percent complete: 13.1%; Average loss: 3.8034
Iteration: 524; Percent complete: 13.1%; Average loss: 3.6513
Iteration: 525; Percent complete: 13.1%; Average loss: 3.7306
Iteration: 526; Percent complete: 13.2%; Average loss: 3.5232
Iteration: 527; Percent complete: 13.2%; Average loss: 3.7586
Iteration: 528; Percent complete: 13.2%; Average loss: 3.6345
Iteration: 529; Percent complete: 13.2%; Average loss: 3.7348
Iteration: 530; Percent complete: 13.2%; Average loss: 3.6078
Iteration: 531; Percent complete: 13.3%; Average loss: 3.6354
Iteration: 532; Percent complete: 13.3%; Average loss: 3.7097
Iteration: 533; Percent complete: 13.3%; Average loss: 3.6355
Iteration: 534; Percent complete: 13.4%; Average loss: 3.5342
Iteration: 535; Percent complete: 13.4%; Average loss: 3.6552
Iteration: 536; Percent complete: 13.4%; Average loss: 3.4923
Iteration: 537; Percent complete: 13.4%; Average loss: 3.5025
Iteration: 538; Percent complete: 13.5%; Average loss: 3.5253
Iteration: 539; Percent complete: 13.5%; Average loss: 3.8002
Iteration: 540; Percent complete: 13.5%; Average loss: 3.4259
Iteration: 541; Percent complete: 13.5%; Average loss: 3.8783
Iteration: 542; Percent complete: 13.6%; Average loss: 3.6831
Iteration: 543; Percent complete: 13.6%; Average loss: 3.8010
Iteration: 544; Percent complete: 13.6%; Average loss: 4.0014
Iteration: 545; Percent complete: 13.6%; Average loss: 3.6643
Iteration: 546; Percent complete: 13.7%; Average loss: 3.4686
Iteration: 547; Percent complete: 13.7%; Average loss: 4.0184
Iteration: 548; Percent complete: 13.7%; Average loss: 3.7910
Iteration: 549; Percent complete: 13.7%; Average loss: 3.9154
Iteration: 550; Percent complete: 13.8%; Average loss: 3.8003
Iteration: 551; Percent complete: 13.8%; Average loss: 3.5892
Iteration: 552; Percent complete: 13.8%; Average loss: 3.7066
Iteration: 553; Percent complete: 13.8%; Average loss: 3.8304
Iteration: 554; Percent complete: 13.9%; Average loss: 3.6913
Iteration: 555; Percent complete: 13.9%; Average loss: 3.6299
Iteration: 556; Percent complete: 13.9%; Average loss: 3.7127
Iteration: 557; Percent complete: 13.9%; Average loss: 3.9960
Iteration: 558; Percent complete: 14.0%; Average loss: 3.8977
Iteration: 559; Percent complete: 14.0%; Average loss: 3.7741
Iteration: 560; Percent complete: 14.0%; Average loss: 3.7830
Iteration: 561; Percent complete: 14.0%; Average loss: 3.7705
Iteration: 562; Percent complete: 14.1%; Average loss: 3.7695
Iteration: 563; Percent complete: 14.1%; Average loss: 3.9734
Iteration: 564; Percent complete: 14.1%; Average loss: 3.7455
Iteration: 565; Percent complete: 14.1%; Average loss: 3.9667
Iteration: 566; Percent complete: 14.1%; Average loss: 3.5774
Iteration: 567; Percent complete: 14.2%; Average loss: 3.7528
Iteration: 568; Percent complete: 14.2%; Average loss: 3.6883
Iteration: 569; Percent complete: 14.2%; Average loss: 3.7331
Iteration: 570; Percent complete: 14.2%; Average loss: 3.5482
Iteration: 571; Percent complete: 14.3%; Average loss: 3.3319
Iteration: 572; Percent complete: 14.3%; Average loss: 3.6765
Iteration: 573; Percent complete: 14.3%; Average loss: 3.5211
Iteration: 574; Percent complete: 14.3%; Average loss: 3.7702
Iteration: 575; Percent complete: 14.4%; Average loss: 3.8108
Iteration: 576; Percent complete: 14.4%; Average loss: 3.8215
Iteration: 577; Percent complete: 14.4%; Average loss: 3.6850
Iteration: 578; Percent complete: 14.4%; Average loss: 3.8227
Iteration: 579; Percent complete: 14.5%; Average loss: 3.5420
Iteration: 580; Percent complete: 14.5%; Average loss: 3.5853
Iteration: 581; Percent complete: 14.5%; Average loss: 3.3015
Iteration: 582; Percent complete: 14.5%; Average loss: 3.5829
Iteration: 583; Percent complete: 14.6%; Average loss: 3.8893
Iteration: 584; Percent complete: 14.6%; Average loss: 3.5899
Iteration: 585; Percent complete: 14.6%; Average loss: 3.7231
Iteration: 586; Percent complete: 14.6%; Average loss: 3.4872
Iteration: 587; Percent complete: 14.7%; Average loss: 3.8011
Iteration: 588; Percent complete: 14.7%; Average loss: 3.8383
Iteration: 589; Percent complete: 14.7%; Average loss: 3.7222
Iteration: 590; Percent complete: 14.8%; Average loss: 3.8363
Iteration: 591; Percent complete: 14.8%; Average loss: 3.7049
Iteration: 592; Percent complete: 14.8%; Average loss: 3.6442
Iteration: 593; Percent complete: 14.8%; Average loss: 3.7405
Iteration: 594; Percent complete: 14.8%; Average loss: 3.7668
Iteration: 595; Percent complete: 14.9%; Average loss: 3.7775
Iteration: 596; Percent complete: 14.9%; Average loss: 3.5802
Iteration: 597; Percent complete: 14.9%; Average loss: 3.8968
Iteration: 598; Percent complete: 14.9%; Average loss: 3.6388
Iteration: 599; Percent complete: 15.0%; Average loss: 3.5596
Iteration: 600; Percent complete: 15.0%; Average loss: 3.8260
Iteration: 601; Percent complete: 15.0%; Average loss: 3.6184
Iteration: 602; Percent complete: 15.0%; Average loss: 3.7620
Iteration: 603; Percent complete: 15.1%; Average loss: 3.5146
Iteration: 604; Percent complete: 15.1%; Average loss: 3.6643
Iteration: 605; Percent complete: 15.1%; Average loss: 3.5151
Iteration: 606; Percent complete: 15.2%; Average loss: 3.9727
Iteration: 607; Percent complete: 15.2%; Average loss: 3.4541
Iteration: 608; Percent complete: 15.2%; Average loss: 3.6500
Iteration: 609; Percent complete: 15.2%; Average loss: 3.8407
Iteration: 610; Percent complete: 15.2%; Average loss: 3.6924
Iteration: 611; Percent complete: 15.3%; Average loss: 3.8288
Iteration: 612; Percent complete: 15.3%; Average loss: 3.5708
Iteration: 613; Percent complete: 15.3%; Average loss: 3.9662
Iteration: 614; Percent complete: 15.3%; Average loss: 3.7712
Iteration: 615; Percent complete: 15.4%; Average loss: 3.5896
Iteration: 616; Percent complete: 15.4%; Average loss: 3.6708
Iteration: 617; Percent complete: 15.4%; Average loss: 3.3829
Iteration: 618; Percent complete: 15.4%; Average loss: 3.3672
Iteration: 619; Percent complete: 15.5%; Average loss: 3.5592
Iteration: 620; Percent complete: 15.5%; Average loss: 3.5960
Iteration: 621; Percent complete: 15.5%; Average loss: 3.7056
Iteration: 622; Percent complete: 15.6%; Average loss: 3.5767
Iteration: 623; Percent complete: 15.6%; Average loss: 3.6003
Iteration: 624; Percent complete: 15.6%; Average loss: 3.4053
Iteration: 625; Percent complete: 15.6%; Average loss: 3.6168
Iteration: 626; Percent complete: 15.7%; Average loss: 3.8760
Iteration: 627; Percent complete: 15.7%; Average loss: 3.7757
Iteration: 628; Percent complete: 15.7%; Average loss: 3.4038
Iteration: 629; Percent complete: 15.7%; Average loss: 3.6747
Iteration: 630; Percent complete: 15.8%; Average loss: 3.5785
Iteration: 631; Percent complete: 15.8%; Average loss: 3.6714
Iteration: 632; Percent complete: 15.8%; Average loss: 3.4819
Iteration: 633; Percent complete: 15.8%; Average loss: 3.8562
Iteration: 634; Percent complete: 15.8%; Average loss: 3.6363
Iteration: 635; Percent complete: 15.9%; Average loss: 3.8210
Iteration: 636; Percent complete: 15.9%; Average loss: 3.5603
Iteration: 637; Percent complete: 15.9%; Average loss: 3.4718
Iteration: 638; Percent complete: 16.0%; Average loss: 3.5398
Iteration: 639; Percent complete: 16.0%; Average loss: 3.8014
Iteration: 640; Percent complete: 16.0%; Average loss: 3.7387
Iteration: 641; Percent complete: 16.0%; Average loss: 3.3103
Iteration: 642; Percent complete: 16.1%; Average loss: 3.5477
Iteration: 643; Percent complete: 16.1%; Average loss: 3.5930
Iteration: 644; Percent complete: 16.1%; Average loss: 3.7211
Iteration: 645; Percent complete: 16.1%; Average loss: 3.5177
Iteration: 646; Percent complete: 16.2%; Average loss: 3.3603
Iteration: 647; Percent complete: 16.2%; Average loss: 3.6840
Iteration: 648; Percent complete: 16.2%; Average loss: 3.7141
Iteration: 649; Percent complete: 16.2%; Average loss: 3.6235
Iteration: 650; Percent complete: 16.2%; Average loss: 3.6609
Iteration: 651; Percent complete: 16.3%; Average loss: 3.6797
Iteration: 652; Percent complete: 16.3%; Average loss: 3.4028
Iteration: 653; Percent complete: 16.3%; Average loss: 3.7093
Iteration: 654; Percent complete: 16.4%; Average loss: 3.5327
Iteration: 655; Percent complete: 16.4%; Average loss: 3.5232
Iteration: 656; Percent complete: 16.4%; Average loss: 3.4665
Iteration: 657; Percent complete: 16.4%; Average loss: 3.5602
Iteration: 658; Percent complete: 16.4%; Average loss: 3.6484
Iteration: 659; Percent complete: 16.5%; Average loss: 3.5103
Iteration: 660; Percent complete: 16.5%; Average loss: 3.7179
Iteration: 661; Percent complete: 16.5%; Average loss: 3.8020
Iteration: 662; Percent complete: 16.6%; Average loss: 3.7197
Iteration: 663; Percent complete: 16.6%; Average loss: 3.8875
Iteration: 664; Percent complete: 16.6%; Average loss: 3.4165
Iteration: 665; Percent complete: 16.6%; Average loss: 3.7912
Iteration: 666; Percent complete: 16.7%; Average loss: 3.7400
Iteration: 667; Percent complete: 16.7%; Average loss: 3.6007
Iteration: 668; Percent complete: 16.7%; Average loss: 3.3483
Iteration: 669; Percent complete: 16.7%; Average loss: 3.5386
Iteration: 670; Percent complete: 16.8%; Average loss: 3.8356
Iteration: 671; Percent complete: 16.8%; Average loss: 3.5827
Iteration: 672; Percent complete: 16.8%; Average loss: 3.8179
Iteration: 673; Percent complete: 16.8%; Average loss: 3.7087
Iteration: 674; Percent complete: 16.9%; Average loss: 3.5298
Iteration: 675; Percent complete: 16.9%; Average loss: 3.8278
Iteration: 676; Percent complete: 16.9%; Average loss: 3.5060
Iteration: 677; Percent complete: 16.9%; Average loss: 3.6074
Iteration: 678; Percent complete: 17.0%; Average loss: 3.5143
Iteration: 679; Percent complete: 17.0%; Average loss: 3.7810
Iteration: 680; Percent complete: 17.0%; Average loss: 3.6118
Iteration: 681; Percent complete: 17.0%; Average loss: 3.7940
Iteration: 682; Percent complete: 17.1%; Average loss: 3.6501
Iteration: 683; Percent complete: 17.1%; Average loss: 3.5430
Iteration: 684; Percent complete: 17.1%; Average loss: 3.5911
Iteration: 685; Percent complete: 17.1%; Average loss: 3.8132
Iteration: 686; Percent complete: 17.2%; Average loss: 3.7408
Iteration: 687; Percent complete: 17.2%; Average loss: 3.4601
Iteration: 688; Percent complete: 17.2%; Average loss: 3.4211
Iteration: 689; Percent complete: 17.2%; Average loss: 3.5452
Iteration: 690; Percent complete: 17.2%; Average loss: 3.4848
Iteration: 691; Percent complete: 17.3%; Average loss: 3.6621
Iteration: 692; Percent complete: 17.3%; Average loss: 3.3564
Iteration: 693; Percent complete: 17.3%; Average loss: 3.6612
Iteration: 694; Percent complete: 17.3%; Average loss: 3.6393
Iteration: 695; Percent complete: 17.4%; Average loss: 3.6401
Iteration: 696; Percent complete: 17.4%; Average loss: 3.4874
Iteration: 697; Percent complete: 17.4%; Average loss: 3.6076
Iteration: 698; Percent complete: 17.4%; Average loss: 3.6549
Iteration: 699; Percent complete: 17.5%; Average loss: 3.7190
Iteration: 700; Percent complete: 17.5%; Average loss: 3.4838
Iteration: 701; Percent complete: 17.5%; Average loss: 3.2584
Iteration: 702; Percent complete: 17.5%; Average loss: 3.3415
Iteration: 703; Percent complete: 17.6%; Average loss: 3.3136
Iteration: 704; Percent complete: 17.6%; Average loss: 3.6190
Iteration: 705; Percent complete: 17.6%; Average loss: 3.3581
Iteration: 706; Percent complete: 17.6%; Average loss: 3.5384
Iteration: 707; Percent complete: 17.7%; Average loss: 3.6031
Iteration: 708; Percent complete: 17.7%; Average loss: 3.3743
Iteration: 709; Percent complete: 17.7%; Average loss: 4.1402
Iteration: 710; Percent complete: 17.8%; Average loss: 3.6570
Iteration: 711; Percent complete: 17.8%; Average loss: 3.6585
Iteration: 712; Percent complete: 17.8%; Average loss: 3.5566
Iteration: 713; Percent complete: 17.8%; Average loss: 3.8146
Iteration: 714; Percent complete: 17.8%; Average loss: 3.8579
Iteration: 715; Percent complete: 17.9%; Average loss: 3.5669
Iteration: 716; Percent complete: 17.9%; Average loss: 3.6869
Iteration: 717; Percent complete: 17.9%; Average loss: 3.7031
Iteration: 718; Percent complete: 17.9%; Average loss: 3.5471
Iteration: 719; Percent complete: 18.0%; Average loss: 3.7741
Iteration: 720; Percent complete: 18.0%; Average loss: 3.7064
Iteration: 721; Percent complete: 18.0%; Average loss: 3.4053
Iteration: 722; Percent complete: 18.1%; Average loss: 3.6208
Iteration: 723; Percent complete: 18.1%; Average loss: 3.9206
Iteration: 724; Percent complete: 18.1%; Average loss: 3.4138
Iteration: 725; Percent complete: 18.1%; Average loss: 3.7051
Iteration: 726; Percent complete: 18.1%; Average loss: 3.5103
Iteration: 727; Percent complete: 18.2%; Average loss: 3.5366
Iteration: 728; Percent complete: 18.2%; Average loss: 3.2374
Iteration: 729; Percent complete: 18.2%; Average loss: 3.3994
Iteration: 730; Percent complete: 18.2%; Average loss: 3.7027
Iteration: 731; Percent complete: 18.3%; Average loss: 3.9243
Iteration: 732; Percent complete: 18.3%; Average loss: 3.4539
Iteration: 733; Percent complete: 18.3%; Average loss: 3.5875
Iteration: 734; Percent complete: 18.4%; Average loss: 3.6370
Iteration: 735; Percent complete: 18.4%; Average loss: 3.7427
Iteration: 736; Percent complete: 18.4%; Average loss: 3.5140
Iteration: 737; Percent complete: 18.4%; Average loss: 3.5601
Iteration: 738; Percent complete: 18.4%; Average loss: 3.5290
Iteration: 739; Percent complete: 18.5%; Average loss: 3.6709
Iteration: 740; Percent complete: 18.5%; Average loss: 3.4954
Iteration: 741; Percent complete: 18.5%; Average loss: 3.7258
Iteration: 742; Percent complete: 18.6%; Average loss: 3.3853
Iteration: 743; Percent complete: 18.6%; Average loss: 3.4530
Iteration: 744; Percent complete: 18.6%; Average loss: 3.8445
Iteration: 745; Percent complete: 18.6%; Average loss: 3.5947
Iteration: 746; Percent complete: 18.6%; Average loss: 3.7880
Iteration: 747; Percent complete: 18.7%; Average loss: 3.6578
Iteration: 748; Percent complete: 18.7%; Average loss: 3.5709
Iteration: 749; Percent complete: 18.7%; Average loss: 3.7174
Iteration: 750; Percent complete: 18.8%; Average loss: 3.6205
Iteration: 751; Percent complete: 18.8%; Average loss: 3.9207
Iteration: 752; Percent complete: 18.8%; Average loss: 3.3684
Iteration: 753; Percent complete: 18.8%; Average loss: 3.7347
Iteration: 754; Percent complete: 18.9%; Average loss: 3.3953
Iteration: 755; Percent complete: 18.9%; Average loss: 3.6418
Iteration: 756; Percent complete: 18.9%; Average loss: 3.6742
Iteration: 757; Percent complete: 18.9%; Average loss: 3.7203
Iteration: 758; Percent complete: 18.9%; Average loss: 3.5889
Iteration: 759; Percent complete: 19.0%; Average loss: 3.3331
Iteration: 760; Percent complete: 19.0%; Average loss: 3.4423
Iteration: 761; Percent complete: 19.0%; Average loss: 3.7556
Iteration: 762; Percent complete: 19.1%; Average loss: 3.5243
Iteration: 763; Percent complete: 19.1%; Average loss: 3.4865
Iteration: 764; Percent complete: 19.1%; Average loss: 3.4383
Iteration: 765; Percent complete: 19.1%; Average loss: 3.6327
Iteration: 766; Percent complete: 19.1%; Average loss: 3.6768
Iteration: 767; Percent complete: 19.2%; Average loss: 3.4112
Iteration: 768; Percent complete: 19.2%; Average loss: 3.3786
Iteration: 769; Percent complete: 19.2%; Average loss: 3.6448
Iteration: 770; Percent complete: 19.2%; Average loss: 3.6389
Iteration: 771; Percent complete: 19.3%; Average loss: 3.7959
Iteration: 772; Percent complete: 19.3%; Average loss: 3.6639
Iteration: 773; Percent complete: 19.3%; Average loss: 3.3948
Iteration: 774; Percent complete: 19.4%; Average loss: 3.6142
Iteration: 775; Percent complete: 19.4%; Average loss: 3.3460
Iteration: 776; Percent complete: 19.4%; Average loss: 3.4153
Iteration: 777; Percent complete: 19.4%; Average loss: 3.5649
Iteration: 778; Percent complete: 19.4%; Average loss: 3.0549
Iteration: 779; Percent complete: 19.5%; Average loss: 3.3801
Iteration: 780; Percent complete: 19.5%; Average loss: 3.5868
Iteration: 781; Percent complete: 19.5%; Average loss: 3.6560
Iteration: 782; Percent complete: 19.6%; Average loss: 4.0150
Iteration: 783; Percent complete: 19.6%; Average loss: 3.4336
Iteration: 784; Percent complete: 19.6%; Average loss: 3.5996
Iteration: 785; Percent complete: 19.6%; Average loss: 3.5736
Iteration: 786; Percent complete: 19.7%; Average loss: 3.9570
Iteration: 787; Percent complete: 19.7%; Average loss: 3.3527
Iteration: 788; Percent complete: 19.7%; Average loss: 3.5091
Iteration: 789; Percent complete: 19.7%; Average loss: 3.5420
Iteration: 790; Percent complete: 19.8%; Average loss: 3.4538
Iteration: 791; Percent complete: 19.8%; Average loss: 3.5085
Iteration: 792; Percent complete: 19.8%; Average loss: 3.7773
Iteration: 793; Percent complete: 19.8%; Average loss: 3.6682
Iteration: 794; Percent complete: 19.9%; Average loss: 3.4078
Iteration: 795; Percent complete: 19.9%; Average loss: 3.6989
Iteration: 796; Percent complete: 19.9%; Average loss: 3.6624
Iteration: 797; Percent complete: 19.9%; Average loss: 3.3440
Iteration: 798; Percent complete: 20.0%; Average loss: 3.4091
Iteration: 799; Percent complete: 20.0%; Average loss: 3.8606
Iteration: 800; Percent complete: 20.0%; Average loss: 3.5693
Iteration: 801; Percent complete: 20.0%; Average loss: 3.5429
Iteration: 802; Percent complete: 20.1%; Average loss: 3.5217
Iteration: 803; Percent complete: 20.1%; Average loss: 3.6944
Iteration: 804; Percent complete: 20.1%; Average loss: 3.5574
Iteration: 805; Percent complete: 20.1%; Average loss: 3.4991
Iteration: 806; Percent complete: 20.2%; Average loss: 3.5495
Iteration: 807; Percent complete: 20.2%; Average loss: 3.8877
Iteration: 808; Percent complete: 20.2%; Average loss: 3.2798
Iteration: 809; Percent complete: 20.2%; Average loss: 4.0319
Iteration: 810; Percent complete: 20.2%; Average loss: 3.7273
Iteration: 811; Percent complete: 20.3%; Average loss: 3.4511
Iteration: 812; Percent complete: 20.3%; Average loss: 3.7143
Iteration: 813; Percent complete: 20.3%; Average loss: 3.5287
Iteration: 814; Percent complete: 20.3%; Average loss: 3.4278
Iteration: 815; Percent complete: 20.4%; Average loss: 3.5237
Iteration: 816; Percent complete: 20.4%; Average loss: 3.6824
Iteration: 817; Percent complete: 20.4%; Average loss: 3.5981
Iteration: 818; Percent complete: 20.4%; Average loss: 3.6322
Iteration: 819; Percent complete: 20.5%; Average loss: 3.5522
Iteration: 820; Percent complete: 20.5%; Average loss: 3.4838
Iteration: 821; Percent complete: 20.5%; Average loss: 3.4496
Iteration: 822; Percent complete: 20.5%; Average loss: 3.4377
Iteration: 823; Percent complete: 20.6%; Average loss: 3.5574
Iteration: 824; Percent complete: 20.6%; Average loss: 3.3739
Iteration: 825; Percent complete: 20.6%; Average loss: 3.4910
Iteration: 826; Percent complete: 20.6%; Average loss: 3.4315
Iteration: 827; Percent complete: 20.7%; Average loss: 3.6305
Iteration: 828; Percent complete: 20.7%; Average loss: 3.5197
Iteration: 829; Percent complete: 20.7%; Average loss: 3.4634
Iteration: 830; Percent complete: 20.8%; Average loss: 3.4037
Iteration: 831; Percent complete: 20.8%; Average loss: 3.6431
Iteration: 832; Percent complete: 20.8%; Average loss: 3.7093
Iteration: 833; Percent complete: 20.8%; Average loss: 3.4993
Iteration: 834; Percent complete: 20.8%; Average loss: 3.6902
Iteration: 835; Percent complete: 20.9%; Average loss: 3.6638
Iteration: 836; Percent complete: 20.9%; Average loss: 3.4649
Iteration: 837; Percent complete: 20.9%; Average loss: 3.6551
Iteration: 838; Percent complete: 20.9%; Average loss: 3.5175
Iteration: 839; Percent complete: 21.0%; Average loss: 3.5063
Iteration: 840; Percent complete: 21.0%; Average loss: 3.5676
Iteration: 841; Percent complete: 21.0%; Average loss: 3.4351
Iteration: 842; Percent complete: 21.1%; Average loss: 3.6413
Iteration: 843; Percent complete: 21.1%; Average loss: 3.7943
Iteration: 844; Percent complete: 21.1%; Average loss: 3.5528
Iteration: 845; Percent complete: 21.1%; Average loss: 3.3326
Iteration: 846; Percent complete: 21.1%; Average loss: 3.6690
Iteration: 847; Percent complete: 21.2%; Average loss: 3.4797
Iteration: 848; Percent complete: 21.2%; Average loss: 3.5358
Iteration: 849; Percent complete: 21.2%; Average loss: 3.7692
Iteration: 850; Percent complete: 21.2%; Average loss: 3.3864
Iteration: 851; Percent complete: 21.3%; Average loss: 3.4590
Iteration: 852; Percent complete: 21.3%; Average loss: 3.7621
Iteration: 853; Percent complete: 21.3%; Average loss: 3.5510
Iteration: 854; Percent complete: 21.3%; Average loss: 3.5115
Iteration: 855; Percent complete: 21.4%; Average loss: 3.8854
Iteration: 856; Percent complete: 21.4%; Average loss: 3.5947
Iteration: 857; Percent complete: 21.4%; Average loss: 3.4474
Iteration: 858; Percent complete: 21.4%; Average loss: 3.5624
Iteration: 859; Percent complete: 21.5%; Average loss: 3.4584
Iteration: 860; Percent complete: 21.5%; Average loss: 3.3964
Iteration: 861; Percent complete: 21.5%; Average loss: 3.7997
Iteration: 862; Percent complete: 21.6%; Average loss: 3.4389
Iteration: 863; Percent complete: 21.6%; Average loss: 3.8095
Iteration: 864; Percent complete: 21.6%; Average loss: 3.7223
Iteration: 865; Percent complete: 21.6%; Average loss: 3.0490
Iteration: 866; Percent complete: 21.6%; Average loss: 3.5104
Iteration: 867; Percent complete: 21.7%; Average loss: 3.6380
Iteration: 868; Percent complete: 21.7%; Average loss: 3.5409
Iteration: 869; Percent complete: 21.7%; Average loss: 3.5852
Iteration: 870; Percent complete: 21.8%; Average loss: 3.5429
Iteration: 871; Percent complete: 21.8%; Average loss: 3.3967
Iteration: 872; Percent complete: 21.8%; Average loss: 3.5671
Iteration: 873; Percent complete: 21.8%; Average loss: 3.8199
Iteration: 874; Percent complete: 21.9%; Average loss: 3.6086
Iteration: 875; Percent complete: 21.9%; Average loss: 3.3901
Iteration: 876; Percent complete: 21.9%; Average loss: 3.3243
Iteration: 877; Percent complete: 21.9%; Average loss: 3.4625
Iteration: 878; Percent complete: 21.9%; Average loss: 3.5529
Iteration: 879; Percent complete: 22.0%; Average loss: 3.2390
Iteration: 880; Percent complete: 22.0%; Average loss: 3.6025
Iteration: 881; Percent complete: 22.0%; Average loss: 3.6321
Iteration: 882; Percent complete: 22.1%; Average loss: 3.3949
Iteration: 883; Percent complete: 22.1%; Average loss: 3.8890
Iteration: 884; Percent complete: 22.1%; Average loss: 3.6950
Iteration: 885; Percent complete: 22.1%; Average loss: 3.3688
Iteration: 886; Percent complete: 22.1%; Average loss: 3.6253
Iteration: 887; Percent complete: 22.2%; Average loss: 3.3235
Iteration: 888; Percent complete: 22.2%; Average loss: 3.6884
Iteration: 889; Percent complete: 22.2%; Average loss: 3.4986
Iteration: 890; Percent complete: 22.2%; Average loss: 3.2977
Iteration: 891; Percent complete: 22.3%; Average loss: 3.4888
Iteration: 892; Percent complete: 22.3%; Average loss: 3.4145
Iteration: 893; Percent complete: 22.3%; Average loss: 3.1096
Iteration: 894; Percent complete: 22.4%; Average loss: 3.3408
Iteration: 895; Percent complete: 22.4%; Average loss: 3.5473
Iteration: 896; Percent complete: 22.4%; Average loss: 3.5614
Iteration: 897; Percent complete: 22.4%; Average loss: 3.6471
Iteration: 898; Percent complete: 22.4%; Average loss: 3.2993
Iteration: 899; Percent complete: 22.5%; Average loss: 3.5873
Iteration: 900; Percent complete: 22.5%; Average loss: 3.8453
Iteration: 901; Percent complete: 22.5%; Average loss: 3.4406
Iteration: 902; Percent complete: 22.6%; Average loss: 3.4832
Iteration: 903; Percent complete: 22.6%; Average loss: 3.4207
Iteration: 904; Percent complete: 22.6%; Average loss: 3.5743
Iteration: 905; Percent complete: 22.6%; Average loss: 3.4582
Iteration: 906; Percent complete: 22.7%; Average loss: 3.3667
Iteration: 907; Percent complete: 22.7%; Average loss: 3.3727
Iteration: 908; Percent complete: 22.7%; Average loss: 3.5824
Iteration: 909; Percent complete: 22.7%; Average loss: 3.5567
Iteration: 910; Percent complete: 22.8%; Average loss: 3.4709
Iteration: 911; Percent complete: 22.8%; Average loss: 3.5178
Iteration: 912; Percent complete: 22.8%; Average loss: 3.6222
Iteration: 913; Percent complete: 22.8%; Average loss: 3.3694
Iteration: 914; Percent complete: 22.9%; Average loss: 3.5517
Iteration: 915; Percent complete: 22.9%; Average loss: 3.5737
Iteration: 916; Percent complete: 22.9%; Average loss: 3.5853
Iteration: 917; Percent complete: 22.9%; Average loss: 3.5079
Iteration: 918; Percent complete: 22.9%; Average loss: 3.4208
Iteration: 919; Percent complete: 23.0%; Average loss: 3.7019
Iteration: 920; Percent complete: 23.0%; Average loss: 3.6271
Iteration: 921; Percent complete: 23.0%; Average loss: 3.2787
Iteration: 922; Percent complete: 23.1%; Average loss: 3.5761
Iteration: 923; Percent complete: 23.1%; Average loss: 3.3220
Iteration: 924; Percent complete: 23.1%; Average loss: 3.2881
Iteration: 925; Percent complete: 23.1%; Average loss: 3.6370
Iteration: 926; Percent complete: 23.2%; Average loss: 3.4291
Iteration: 927; Percent complete: 23.2%; Average loss: 3.5912
Iteration: 928; Percent complete: 23.2%; Average loss: 3.5802
Iteration: 929; Percent complete: 23.2%; Average loss: 3.5022
Iteration: 930; Percent complete: 23.2%; Average loss: 3.4319
Iteration: 931; Percent complete: 23.3%; Average loss: 3.4474
Iteration: 932; Percent complete: 23.3%; Average loss: 3.4339
Iteration: 933; Percent complete: 23.3%; Average loss: 3.1553
Iteration: 934; Percent complete: 23.4%; Average loss: 3.4027
Iteration: 935; Percent complete: 23.4%; Average loss: 3.8287
Iteration: 936; Percent complete: 23.4%; Average loss: 3.6209
Iteration: 937; Percent complete: 23.4%; Average loss: 3.4450
Iteration: 938; Percent complete: 23.4%; Average loss: 3.5986
Iteration: 939; Percent complete: 23.5%; Average loss: 3.6583
Iteration: 940; Percent complete: 23.5%; Average loss: 3.4533
Iteration: 941; Percent complete: 23.5%; Average loss: 3.5109
Iteration: 942; Percent complete: 23.5%; Average loss: 3.4085
Iteration: 943; Percent complete: 23.6%; Average loss: 3.4424
Iteration: 944; Percent complete: 23.6%; Average loss: 3.5572
Iteration: 945; Percent complete: 23.6%; Average loss: 3.4118
Iteration: 946; Percent complete: 23.6%; Average loss: 3.3752
Iteration: 947; Percent complete: 23.7%; Average loss: 3.2920
Iteration: 948; Percent complete: 23.7%; Average loss: 3.7975
Iteration: 949; Percent complete: 23.7%; Average loss: 3.5973
Iteration: 950; Percent complete: 23.8%; Average loss: 3.4450
Iteration: 951; Percent complete: 23.8%; Average loss: 3.8621
Iteration: 952; Percent complete: 23.8%; Average loss: 3.3209
Iteration: 953; Percent complete: 23.8%; Average loss: 3.3641
Iteration: 954; Percent complete: 23.8%; Average loss: 3.2609
Iteration: 955; Percent complete: 23.9%; Average loss: 3.4884
Iteration: 956; Percent complete: 23.9%; Average loss: 3.6754
Iteration: 957; Percent complete: 23.9%; Average loss: 3.3461
Iteration: 958; Percent complete: 23.9%; Average loss: 3.4707
Iteration: 959; Percent complete: 24.0%; Average loss: 3.4884
Iteration: 960; Percent complete: 24.0%; Average loss: 3.5299
Iteration: 961; Percent complete: 24.0%; Average loss: 3.3482
Iteration: 962; Percent complete: 24.1%; Average loss: 3.3945
Iteration: 963; Percent complete: 24.1%; Average loss: 3.5881
Iteration: 964; Percent complete: 24.1%; Average loss: 3.3144
Iteration: 965; Percent complete: 24.1%; Average loss: 3.4570
Iteration: 966; Percent complete: 24.1%; Average loss: 3.2718
Iteration: 967; Percent complete: 24.2%; Average loss: 3.8598
Iteration: 968; Percent complete: 24.2%; Average loss: 3.3648
Iteration: 969; Percent complete: 24.2%; Average loss: 3.3774
Iteration: 970; Percent complete: 24.2%; Average loss: 3.8062
Iteration: 971; Percent complete: 24.3%; Average loss: 3.5632
Iteration: 972; Percent complete: 24.3%; Average loss: 3.2860
Iteration: 973; Percent complete: 24.3%; Average loss: 3.3954
Iteration: 974; Percent complete: 24.3%; Average loss: 3.6381
Iteration: 975; Percent complete: 24.4%; Average loss: 3.4003
Iteration: 976; Percent complete: 24.4%; Average loss: 3.5173
Iteration: 977; Percent complete: 24.4%; Average loss: 3.5985
Iteration: 978; Percent complete: 24.4%; Average loss: 3.5645
Iteration: 979; Percent complete: 24.5%; Average loss: 3.2724
Iteration: 980; Percent complete: 24.5%; Average loss: 3.5022
Iteration: 981; Percent complete: 24.5%; Average loss: 3.7490
Iteration: 982; Percent complete: 24.6%; Average loss: 3.5153
Iteration: 983; Percent complete: 24.6%; Average loss: 3.3242
Iteration: 984; Percent complete: 24.6%; Average loss: 3.4940
Iteration: 985; Percent complete: 24.6%; Average loss: 3.2924
Iteration: 986; Percent complete: 24.6%; Average loss: 3.6159
Iteration: 987; Percent complete: 24.7%; Average loss: 3.5092
Iteration: 988; Percent complete: 24.7%; Average loss: 3.1650
Iteration: 989; Percent complete: 24.7%; Average loss: 3.4428
Iteration: 990; Percent complete: 24.8%; Average loss: 3.4637
Iteration: 991; Percent complete: 24.8%; Average loss: 3.4727
Iteration: 992; Percent complete: 24.8%; Average loss: 3.6312
Iteration: 993; Percent complete: 24.8%; Average loss: 3.4884
Iteration: 994; Percent complete: 24.9%; Average loss: 3.5849
Iteration: 995; Percent complete: 24.9%; Average loss: 3.3557
Iteration: 996; Percent complete: 24.9%; Average loss: 3.2668
Iteration: 997; Percent complete: 24.9%; Average loss: 3.3219
Iteration: 998; Percent complete: 24.9%; Average loss: 3.3498
Iteration: 999; Percent complete: 25.0%; Average loss: 3.2003
Iteration: 1000; Percent complete: 25.0%; Average loss: 3.4872
Iteration: 1001; Percent complete: 25.0%; Average loss: 3.8544
Iteration: 1002; Percent complete: 25.1%; Average loss: 3.6656
Iteration: 1003; Percent complete: 25.1%; Average loss: 3.5623
Iteration: 1004; Percent complete: 25.1%; Average loss: 3.4700
Iteration: 1005; Percent complete: 25.1%; Average loss: 3.6828
Iteration: 1006; Percent complete: 25.1%; Average loss: 3.3585
Iteration: 1007; Percent complete: 25.2%; Average loss: 3.7551
Iteration: 1008; Percent complete: 25.2%; Average loss: 3.2769
Iteration: 1009; Percent complete: 25.2%; Average loss: 3.4719
Iteration: 1010; Percent complete: 25.2%; Average loss: 3.5711
Iteration: 1011; Percent complete: 25.3%; Average loss: 3.2510
Iteration: 1012; Percent complete: 25.3%; Average loss: 3.6189
Iteration: 1013; Percent complete: 25.3%; Average loss: 3.4905
Iteration: 1014; Percent complete: 25.4%; Average loss: 3.6845
Iteration: 1015; Percent complete: 25.4%; Average loss: 3.1448
Iteration: 1016; Percent complete: 25.4%; Average loss: 3.3185
Iteration: 1017; Percent complete: 25.4%; Average loss: 3.6900
Iteration: 1018; Percent complete: 25.4%; Average loss: 3.4992
Iteration: 1019; Percent complete: 25.5%; Average loss: 3.5172
Iteration: 1020; Percent complete: 25.5%; Average loss: 3.4248
Iteration: 1021; Percent complete: 25.5%; Average loss: 3.6229
Iteration: 1022; Percent complete: 25.6%; Average loss: 3.4687
Iteration: 1023; Percent complete: 25.6%; Average loss: 3.4424
Iteration: 1024; Percent complete: 25.6%; Average loss: 3.8235
Iteration: 1025; Percent complete: 25.6%; Average loss: 3.4971
Iteration: 1026; Percent complete: 25.7%; Average loss: 3.3183
Iteration: 1027; Percent complete: 25.7%; Average loss: 3.3431
Iteration: 1028; Percent complete: 25.7%; Average loss: 3.6884
Iteration: 1029; Percent complete: 25.7%; Average loss: 3.5919
Iteration: 1030; Percent complete: 25.8%; Average loss: 3.4621
Iteration: 1031; Percent complete: 25.8%; Average loss: 3.8175
Iteration: 1032; Percent complete: 25.8%; Average loss: 3.4358
Iteration: 1033; Percent complete: 25.8%; Average loss: 3.0230
Iteration: 1034; Percent complete: 25.9%; Average loss: 3.5215
Iteration: 1035; Percent complete: 25.9%; Average loss: 3.6084
Iteration: 1036; Percent complete: 25.9%; Average loss: 3.4859
Iteration: 1037; Percent complete: 25.9%; Average loss: 3.6356
Iteration: 1038; Percent complete: 25.9%; Average loss: 3.8803
Iteration: 1039; Percent complete: 26.0%; Average loss: 3.6233
Iteration: 1040; Percent complete: 26.0%; Average loss: 3.6527
Iteration: 1041; Percent complete: 26.0%; Average loss: 3.2279
Iteration: 1042; Percent complete: 26.1%; Average loss: 3.1798
Iteration: 1043; Percent complete: 26.1%; Average loss: 3.5130
Iteration: 1044; Percent complete: 26.1%; Average loss: 3.5915
Iteration: 1045; Percent complete: 26.1%; Average loss: 3.3605
Iteration: 1046; Percent complete: 26.2%; Average loss: 3.4311
Iteration: 1047; Percent complete: 26.2%; Average loss: 3.3859
Iteration: 1048; Percent complete: 26.2%; Average loss: 3.3836
Iteration: 1049; Percent complete: 26.2%; Average loss: 3.4402
Iteration: 1050; Percent complete: 26.2%; Average loss: 3.5923
Iteration: 1051; Percent complete: 26.3%; Average loss: 3.7887
Iteration: 1052; Percent complete: 26.3%; Average loss: 3.5061
Iteration: 1053; Percent complete: 26.3%; Average loss: 3.4963
Iteration: 1054; Percent complete: 26.4%; Average loss: 3.3367
Iteration: 1055; Percent complete: 26.4%; Average loss: 3.5048
Iteration: 1056; Percent complete: 26.4%; Average loss: 3.4390
Iteration: 1057; Percent complete: 26.4%; Average loss: 3.2311
Iteration: 1058; Percent complete: 26.5%; Average loss: 3.6569
Iteration: 1059; Percent complete: 26.5%; Average loss: 3.3164
Iteration: 1060; Percent complete: 26.5%; Average loss: 3.5268
Iteration: 1061; Percent complete: 26.5%; Average loss: 3.5255
Iteration: 1062; Percent complete: 26.6%; Average loss: 3.2869
Iteration: 1063; Percent complete: 26.6%; Average loss: 3.4248
Iteration: 1064; Percent complete: 26.6%; Average loss: 3.2704
Iteration: 1065; Percent complete: 26.6%; Average loss: 3.4290
Iteration: 1066; Percent complete: 26.7%; Average loss: 3.5003
Iteration: 1067; Percent complete: 26.7%; Average loss: 3.3283
Iteration: 1068; Percent complete: 26.7%; Average loss: 3.7557
Iteration: 1069; Percent complete: 26.7%; Average loss: 3.4967
Iteration: 1070; Percent complete: 26.8%; Average loss: 3.4647
Iteration: 1071; Percent complete: 26.8%; Average loss: 3.7736
Iteration: 1072; Percent complete: 26.8%; Average loss: 3.5138
Iteration: 1073; Percent complete: 26.8%; Average loss: 3.5193
Iteration: 1074; Percent complete: 26.9%; Average loss: 3.5778
Iteration: 1075; Percent complete: 26.9%; Average loss: 3.5531
Iteration: 1076; Percent complete: 26.9%; Average loss: 3.4109
Iteration: 1077; Percent complete: 26.9%; Average loss: 3.4992
Iteration: 1078; Percent complete: 27.0%; Average loss: 3.5084
Iteration: 1079; Percent complete: 27.0%; Average loss: 3.4643
Iteration: 1080; Percent complete: 27.0%; Average loss: 3.0723
Iteration: 1081; Percent complete: 27.0%; Average loss: 3.4982
Iteration: 1082; Percent complete: 27.1%; Average loss: 3.4758
Iteration: 1083; Percent complete: 27.1%; Average loss: 3.5815
Iteration: 1084; Percent complete: 27.1%; Average loss: 3.6103
Iteration: 1085; Percent complete: 27.1%; Average loss: 3.3178
Iteration: 1086; Percent complete: 27.2%; Average loss: 3.2966
Iteration: 1087; Percent complete: 27.2%; Average loss: 3.6029
Iteration: 1088; Percent complete: 27.2%; Average loss: 3.3743
Iteration: 1089; Percent complete: 27.2%; Average loss: 3.1857
Iteration: 1090; Percent complete: 27.3%; Average loss: 3.3934
Iteration: 1091; Percent complete: 27.3%; Average loss: 3.1867
Iteration: 1092; Percent complete: 27.3%; Average loss: 3.5611
Iteration: 1093; Percent complete: 27.3%; Average loss: 3.4533
Iteration: 1094; Percent complete: 27.4%; Average loss: 3.4705
Iteration: 1095; Percent complete: 27.4%; Average loss: 3.7388
Iteration: 1096; Percent complete: 27.4%; Average loss: 3.3847
Iteration: 1097; Percent complete: 27.4%; Average loss: 3.5296
Iteration: 1098; Percent complete: 27.5%; Average loss: 3.5349
Iteration: 1099; Percent complete: 27.5%; Average loss: 3.2996
Iteration: 1100; Percent complete: 27.5%; Average loss: 3.5545
Iteration: 1101; Percent complete: 27.5%; Average loss: 3.3433
Iteration: 1102; Percent complete: 27.6%; Average loss: 3.3553
Iteration: 1103; Percent complete: 27.6%; Average loss: 3.1691
Iteration: 1104; Percent complete: 27.6%; Average loss: 3.4612
Iteration: 1105; Percent complete: 27.6%; Average loss: 3.4606
Iteration: 1106; Percent complete: 27.7%; Average loss: 3.3276
Iteration: 1107; Percent complete: 27.7%; Average loss: 3.4118
Iteration: 1108; Percent complete: 27.7%; Average loss: 3.5662
Iteration: 1109; Percent complete: 27.7%; Average loss: 3.3092
Iteration: 1110; Percent complete: 27.8%; Average loss: 3.5933
Iteration: 1111; Percent complete: 27.8%; Average loss: 3.2453
Iteration: 1112; Percent complete: 27.8%; Average loss: 3.6600
Iteration: 1113; Percent complete: 27.8%; Average loss: 3.6058
Iteration: 1114; Percent complete: 27.9%; Average loss: 3.2881
Iteration: 1115; Percent complete: 27.9%; Average loss: 3.5583
Iteration: 1116; Percent complete: 27.9%; Average loss: 3.3307
Iteration: 1117; Percent complete: 27.9%; Average loss: 3.5117
Iteration: 1118; Percent complete: 28.0%; Average loss: 2.9897
Iteration: 1119; Percent complete: 28.0%; Average loss: 3.5887
Iteration: 1120; Percent complete: 28.0%; Average loss: 3.2526
Iteration: 1121; Percent complete: 28.0%; Average loss: 3.4913
Iteration: 1122; Percent complete: 28.1%; Average loss: 3.4393
Iteration: 1123; Percent complete: 28.1%; Average loss: 3.3721
Iteration: 1124; Percent complete: 28.1%; Average loss: 3.3686
Iteration: 1125; Percent complete: 28.1%; Average loss: 3.3339
Iteration: 1126; Percent complete: 28.1%; Average loss: 3.4897
Iteration: 1127; Percent complete: 28.2%; Average loss: 3.6130
Iteration: 1128; Percent complete: 28.2%; Average loss: 3.3740
Iteration: 1129; Percent complete: 28.2%; Average loss: 3.4080
Iteration: 1130; Percent complete: 28.2%; Average loss: 3.5162
Iteration: 1131; Percent complete: 28.3%; Average loss: 3.5502
Iteration: 1132; Percent complete: 28.3%; Average loss: 3.1863
Iteration: 1133; Percent complete: 28.3%; Average loss: 3.4661
Iteration: 1134; Percent complete: 28.3%; Average loss: 3.3546
Iteration: 1135; Percent complete: 28.4%; Average loss: 3.2590
Iteration: 1136; Percent complete: 28.4%; Average loss: 3.2258
Iteration: 1137; Percent complete: 28.4%; Average loss: 3.4518
Iteration: 1138; Percent complete: 28.4%; Average loss: 3.3536
Iteration: 1139; Percent complete: 28.5%; Average loss: 3.2633
Iteration: 1140; Percent complete: 28.5%; Average loss: 3.5984
Iteration: 1141; Percent complete: 28.5%; Average loss: 3.8193
Iteration: 1142; Percent complete: 28.5%; Average loss: 3.4040
Iteration: 1143; Percent complete: 28.6%; Average loss: 3.4012
Iteration: 1144; Percent complete: 28.6%; Average loss: 3.5520
Iteration: 1145; Percent complete: 28.6%; Average loss: 3.2561
Iteration: 1146; Percent complete: 28.6%; Average loss: 3.4164
Iteration: 1147; Percent complete: 28.7%; Average loss: 3.4309
Iteration: 1148; Percent complete: 28.7%; Average loss: 3.4156
Iteration: 1149; Percent complete: 28.7%; Average loss: 3.5077
Iteration: 1150; Percent complete: 28.7%; Average loss: 3.2217
Iteration: 1151; Percent complete: 28.8%; Average loss: 3.3073
Iteration: 1152; Percent complete: 28.8%; Average loss: 3.6923
Iteration: 1153; Percent complete: 28.8%; Average loss: 3.3872
Iteration: 1154; Percent complete: 28.8%; Average loss: 3.5498
Iteration: 1155; Percent complete: 28.9%; Average loss: 3.5230
Iteration: 1156; Percent complete: 28.9%; Average loss: 3.3777
Iteration: 1157; Percent complete: 28.9%; Average loss: 3.4221
Iteration: 1158; Percent complete: 28.9%; Average loss: 3.5279
Iteration: 1159; Percent complete: 29.0%; Average loss: 3.3207
Iteration: 1160; Percent complete: 29.0%; Average loss: 3.4095
Iteration: 1161; Percent complete: 29.0%; Average loss: 3.6650
Iteration: 1162; Percent complete: 29.0%; Average loss: 3.2738
Iteration: 1163; Percent complete: 29.1%; Average loss: 3.7024
Iteration: 1164; Percent complete: 29.1%; Average loss: 3.4286
Iteration: 1165; Percent complete: 29.1%; Average loss: 3.3582
Iteration: 1166; Percent complete: 29.1%; Average loss: 3.1744
Iteration: 1167; Percent complete: 29.2%; Average loss: 3.4612
Iteration: 1168; Percent complete: 29.2%; Average loss: 3.4571
Iteration: 1169; Percent complete: 29.2%; Average loss: 3.3405
Iteration: 1170; Percent complete: 29.2%; Average loss: 3.5395
Iteration: 1171; Percent complete: 29.3%; Average loss: 3.3033
Iteration: 1172; Percent complete: 29.3%; Average loss: 3.4264
Iteration: 1173; Percent complete: 29.3%; Average loss: 3.3294
Iteration: 1174; Percent complete: 29.3%; Average loss: 3.2282
Iteration: 1175; Percent complete: 29.4%; Average loss: 3.4357
Iteration: 1176; Percent complete: 29.4%; Average loss: 3.4345
Iteration: 1177; Percent complete: 29.4%; Average loss: 3.7204
Iteration: 1178; Percent complete: 29.4%; Average loss: 3.5692
Iteration: 1179; Percent complete: 29.5%; Average loss: 3.3134
Iteration: 1180; Percent complete: 29.5%; Average loss: 3.6395
Iteration: 1181; Percent complete: 29.5%; Average loss: 3.4991
Iteration: 1182; Percent complete: 29.5%; Average loss: 3.6298
Iteration: 1183; Percent complete: 29.6%; Average loss: 3.6161
Iteration: 1184; Percent complete: 29.6%; Average loss: 3.4503
Iteration: 1185; Percent complete: 29.6%; Average loss: 3.3284
Iteration: 1186; Percent complete: 29.6%; Average loss: 3.3689
Iteration: 1187; Percent complete: 29.7%; Average loss: 3.5950
Iteration: 1188; Percent complete: 29.7%; Average loss: 3.4256
Iteration: 1189; Percent complete: 29.7%; Average loss: 3.6191
Iteration: 1190; Percent complete: 29.8%; Average loss: 3.4404
Iteration: 1191; Percent complete: 29.8%; Average loss: 3.3747
Iteration: 1192; Percent complete: 29.8%; Average loss: 3.3502
Iteration: 1193; Percent complete: 29.8%; Average loss: 3.3788
Iteration: 1194; Percent complete: 29.8%; Average loss: 3.2694
Iteration: 1195; Percent complete: 29.9%; Average loss: 3.2853
Iteration: 1196; Percent complete: 29.9%; Average loss: 3.3277
Iteration: 1197; Percent complete: 29.9%; Average loss: 3.2933
Iteration: 1198; Percent complete: 29.9%; Average loss: 3.5857
Iteration: 1199; Percent complete: 30.0%; Average loss: 3.5407
Iteration: 1200; Percent complete: 30.0%; Average loss: 3.6762
Iteration: 1201; Percent complete: 30.0%; Average loss: 3.3860
Iteration: 1202; Percent complete: 30.0%; Average loss: 3.3208
Iteration: 1203; Percent complete: 30.1%; Average loss: 3.5518
Iteration: 1204; Percent complete: 30.1%; Average loss: 3.7564
Iteration: 1205; Percent complete: 30.1%; Average loss: 3.4354
Iteration: 1206; Percent complete: 30.1%; Average loss: 3.3566
Iteration: 1207; Percent complete: 30.2%; Average loss: 3.2711
Iteration: 1208; Percent complete: 30.2%; Average loss: 3.3205
Iteration: 1209; Percent complete: 30.2%; Average loss: 3.5178
Iteration: 1210; Percent complete: 30.2%; Average loss: 3.4496
Iteration: 1211; Percent complete: 30.3%; Average loss: 3.4019
Iteration: 1212; Percent complete: 30.3%; Average loss: 3.5852
Iteration: 1213; Percent complete: 30.3%; Average loss: 3.1096
Iteration: 1214; Percent complete: 30.3%; Average loss: 3.3044
Iteration: 1215; Percent complete: 30.4%; Average loss: 3.4885
Iteration: 1216; Percent complete: 30.4%; Average loss: 3.7294
Iteration: 1217; Percent complete: 30.4%; Average loss: 3.2810
Iteration: 1218; Percent complete: 30.4%; Average loss: 3.5160
Iteration: 1219; Percent complete: 30.5%; Average loss: 3.3837
Iteration: 1220; Percent complete: 30.5%; Average loss: 3.3137
Iteration: 1221; Percent complete: 30.5%; Average loss: 3.5503
Iteration: 1222; Percent complete: 30.6%; Average loss: 3.4638
Iteration: 1223; Percent complete: 30.6%; Average loss: 3.2969
Iteration: 1224; Percent complete: 30.6%; Average loss: 3.5458
Iteration: 1225; Percent complete: 30.6%; Average loss: 3.1569
Iteration: 1226; Percent complete: 30.6%; Average loss: 3.3007
Iteration: 1227; Percent complete: 30.7%; Average loss: 3.1881
Iteration: 1228; Percent complete: 30.7%; Average loss: 3.4935
Iteration: 1229; Percent complete: 30.7%; Average loss: 3.1512
Iteration: 1230; Percent complete: 30.8%; Average loss: 3.3010
Iteration: 1231; Percent complete: 30.8%; Average loss: 3.6302
Iteration: 1232; Percent complete: 30.8%; Average loss: 3.5801
Iteration: 1233; Percent complete: 30.8%; Average loss: 3.4603
Iteration: 1234; Percent complete: 30.9%; Average loss: 3.5682
Iteration: 1235; Percent complete: 30.9%; Average loss: 3.3117
Iteration: 1236; Percent complete: 30.9%; Average loss: 3.3098
Iteration: 1237; Percent complete: 30.9%; Average loss: 3.4507
Iteration: 1238; Percent complete: 30.9%; Average loss: 3.4023
Iteration: 1239; Percent complete: 31.0%; Average loss: 3.4576
Iteration: 1240; Percent complete: 31.0%; Average loss: 3.6101
Iteration: 1241; Percent complete: 31.0%; Average loss: 3.2351
Iteration: 1242; Percent complete: 31.1%; Average loss: 3.4683
Iteration: 1243; Percent complete: 31.1%; Average loss: 3.5446
Iteration: 1244; Percent complete: 31.1%; Average loss: 3.3684
Iteration: 1245; Percent complete: 31.1%; Average loss: 3.5095
Iteration: 1246; Percent complete: 31.1%; Average loss: 3.3798
Iteration: 1247; Percent complete: 31.2%; Average loss: 3.2559
Iteration: 1248; Percent complete: 31.2%; Average loss: 3.3188
Iteration: 1249; Percent complete: 31.2%; Average loss: 3.1712
Iteration: 1250; Percent complete: 31.2%; Average loss: 3.2782
Iteration: 1251; Percent complete: 31.3%; Average loss: 3.3124
Iteration: 1252; Percent complete: 31.3%; Average loss: 3.3001
Iteration: 1253; Percent complete: 31.3%; Average loss: 3.6182
Iteration: 1254; Percent complete: 31.4%; Average loss: 3.6227
Iteration: 1255; Percent complete: 31.4%; Average loss: 3.2699
Iteration: 1256; Percent complete: 31.4%; Average loss: 3.4462
Iteration: 1257; Percent complete: 31.4%; Average loss: 3.5194
Iteration: 1258; Percent complete: 31.4%; Average loss: 3.2072
Iteration: 1259; Percent complete: 31.5%; Average loss: 3.7606
Iteration: 1260; Percent complete: 31.5%; Average loss: 3.4329
Iteration: 1261; Percent complete: 31.5%; Average loss: 3.3591
Iteration: 1262; Percent complete: 31.6%; Average loss: 3.4238
Iteration: 1263; Percent complete: 31.6%; Average loss: 3.2219
Iteration: 1264; Percent complete: 31.6%; Average loss: 3.2932
Iteration: 1265; Percent complete: 31.6%; Average loss: 3.4036
Iteration: 1266; Percent complete: 31.6%; Average loss: 3.4101
Iteration: 1267; Percent complete: 31.7%; Average loss: 3.2133
Iteration: 1268; Percent complete: 31.7%; Average loss: 3.4745
Iteration: 1269; Percent complete: 31.7%; Average loss: 3.4521
Iteration: 1270; Percent complete: 31.8%; Average loss: 3.3188
Iteration: 1271; Percent complete: 31.8%; Average loss: 3.2920
Iteration: 1272; Percent complete: 31.8%; Average loss: 3.3997
Iteration: 1273; Percent complete: 31.8%; Average loss: 3.2646
Iteration: 1274; Percent complete: 31.9%; Average loss: 3.2926
Iteration: 1275; Percent complete: 31.9%; Average loss: 3.2209
Iteration: 1276; Percent complete: 31.9%; Average loss: 3.1511
Iteration: 1277; Percent complete: 31.9%; Average loss: 3.6325
Iteration: 1278; Percent complete: 31.9%; Average loss: 3.3733
Iteration: 1279; Percent complete: 32.0%; Average loss: 3.1905
Iteration: 1280; Percent complete: 32.0%; Average loss: 3.2734
Iteration: 1281; Percent complete: 32.0%; Average loss: 3.6147
Iteration: 1282; Percent complete: 32.0%; Average loss: 3.5460
Iteration: 1283; Percent complete: 32.1%; Average loss: 3.2406
Iteration: 1284; Percent complete: 32.1%; Average loss: 3.2533
Iteration: 1285; Percent complete: 32.1%; Average loss: 3.4935
Iteration: 1286; Percent complete: 32.1%; Average loss: 3.4593
Iteration: 1287; Percent complete: 32.2%; Average loss: 3.2415
Iteration: 1288; Percent complete: 32.2%; Average loss: 3.4803
Iteration: 1289; Percent complete: 32.2%; Average loss: 3.6386
Iteration: 1290; Percent complete: 32.2%; Average loss: 3.5069
Iteration: 1291; Percent complete: 32.3%; Average loss: 3.3806
Iteration: 1292; Percent complete: 32.3%; Average loss: 3.2001
Iteration: 1293; Percent complete: 32.3%; Average loss: 3.4048
Iteration: 1294; Percent complete: 32.4%; Average loss: 3.4837
Iteration: 1295; Percent complete: 32.4%; Average loss: 3.4840
Iteration: 1296; Percent complete: 32.4%; Average loss: 3.2480
Iteration: 1297; Percent complete: 32.4%; Average loss: 3.3299
Iteration: 1298; Percent complete: 32.5%; Average loss: 3.1023
Iteration: 1299; Percent complete: 32.5%; Average loss: 3.1146
Iteration: 1300; Percent complete: 32.5%; Average loss: 3.6748
Iteration: 1301; Percent complete: 32.5%; Average loss: 3.7209
Iteration: 1302; Percent complete: 32.6%; Average loss: 3.4553
Iteration: 1303; Percent complete: 32.6%; Average loss: 3.5933
Iteration: 1304; Percent complete: 32.6%; Average loss: 3.5286
Iteration: 1305; Percent complete: 32.6%; Average loss: 3.4181
Iteration: 1306; Percent complete: 32.6%; Average loss: 3.4865
Iteration: 1307; Percent complete: 32.7%; Average loss: 3.5189
Iteration: 1308; Percent complete: 32.7%; Average loss: 3.5368
Iteration: 1309; Percent complete: 32.7%; Average loss: 3.4270
Iteration: 1310; Percent complete: 32.8%; Average loss: 3.5959
Iteration: 1311; Percent complete: 32.8%; Average loss: 3.0740
Iteration: 1312; Percent complete: 32.8%; Average loss: 3.3799
Iteration: 1313; Percent complete: 32.8%; Average loss: 3.4871
Iteration: 1314; Percent complete: 32.9%; Average loss: 3.3671
Iteration: 1315; Percent complete: 32.9%; Average loss: 3.4274
Iteration: 1316; Percent complete: 32.9%; Average loss: 3.2748
Iteration: 1317; Percent complete: 32.9%; Average loss: 3.6972
Iteration: 1318; Percent complete: 33.0%; Average loss: 3.2400
Iteration: 1319; Percent complete: 33.0%; Average loss: 3.4576
Iteration: 1320; Percent complete: 33.0%; Average loss: 3.0902
Iteration: 1321; Percent complete: 33.0%; Average loss: 3.1947
Iteration: 1322; Percent complete: 33.1%; Average loss: 3.3297
Iteration: 1323; Percent complete: 33.1%; Average loss: 3.3101
Iteration: 1324; Percent complete: 33.1%; Average loss: 3.5221
Iteration: 1325; Percent complete: 33.1%; Average loss: 3.2948
Iteration: 1326; Percent complete: 33.1%; Average loss: 3.5066
Iteration: 1327; Percent complete: 33.2%; Average loss: 3.3889
Iteration: 1328; Percent complete: 33.2%; Average loss: 3.2062
Iteration: 1329; Percent complete: 33.2%; Average loss: 3.4641
Iteration: 1330; Percent complete: 33.2%; Average loss: 3.1375
Iteration: 1331; Percent complete: 33.3%; Average loss: 3.4720
Iteration: 1332; Percent complete: 33.3%; Average loss: 3.4578
Iteration: 1333; Percent complete: 33.3%; Average loss: 3.2677
Iteration: 1334; Percent complete: 33.4%; Average loss: 3.1549
Iteration: 1335; Percent complete: 33.4%; Average loss: 3.3338
Iteration: 1336; Percent complete: 33.4%; Average loss: 3.2325
Iteration: 1337; Percent complete: 33.4%; Average loss: 3.1854
Iteration: 1338; Percent complete: 33.5%; Average loss: 3.2034
Iteration: 1339; Percent complete: 33.5%; Average loss: 3.4426
Iteration: 1340; Percent complete: 33.5%; Average loss: 3.3887
Iteration: 1341; Percent complete: 33.5%; Average loss: 3.2303
Iteration: 1342; Percent complete: 33.6%; Average loss: 3.5545
Iteration: 1343; Percent complete: 33.6%; Average loss: 3.3741
Iteration: 1344; Percent complete: 33.6%; Average loss: 3.7304
Iteration: 1345; Percent complete: 33.6%; Average loss: 3.4930
Iteration: 1346; Percent complete: 33.7%; Average loss: 3.2414
Iteration: 1347; Percent complete: 33.7%; Average loss: 3.4180
Iteration: 1348; Percent complete: 33.7%; Average loss: 3.3882
Iteration: 1349; Percent complete: 33.7%; Average loss: 3.3570
Iteration: 1350; Percent complete: 33.8%; Average loss: 3.1598
Iteration: 1351; Percent complete: 33.8%; Average loss: 3.1032
Iteration: 1352; Percent complete: 33.8%; Average loss: 3.3302
Iteration: 1353; Percent complete: 33.8%; Average loss: 3.0545
Iteration: 1354; Percent complete: 33.9%; Average loss: 3.2856
Iteration: 1355; Percent complete: 33.9%; Average loss: 3.6337
Iteration: 1356; Percent complete: 33.9%; Average loss: 3.3797
Iteration: 1357; Percent complete: 33.9%; Average loss: 3.2831
Iteration: 1358; Percent complete: 34.0%; Average loss: 3.4590
Iteration: 1359; Percent complete: 34.0%; Average loss: 3.0371
Iteration: 1360; Percent complete: 34.0%; Average loss: 3.4222
Iteration: 1361; Percent complete: 34.0%; Average loss: 3.3357
Iteration: 1362; Percent complete: 34.1%; Average loss: 3.4398
Iteration: 1363; Percent complete: 34.1%; Average loss: 3.3684
Iteration: 1364; Percent complete: 34.1%; Average loss: 3.2454
Iteration: 1365; Percent complete: 34.1%; Average loss: 3.3550
Iteration: 1366; Percent complete: 34.2%; Average loss: 3.2988
Iteration: 1367; Percent complete: 34.2%; Average loss: 3.2793
Iteration: 1368; Percent complete: 34.2%; Average loss: 3.3623
Iteration: 1369; Percent complete: 34.2%; Average loss: 3.1654
Iteration: 1370; Percent complete: 34.2%; Average loss: 3.4821
Iteration: 1371; Percent complete: 34.3%; Average loss: 3.4916
Iteration: 1372; Percent complete: 34.3%; Average loss: 3.2444
Iteration: 1373; Percent complete: 34.3%; Average loss: 3.2431
Iteration: 1374; Percent complete: 34.4%; Average loss: 3.3614
Iteration: 1375; Percent complete: 34.4%; Average loss: 3.1599
Iteration: 1376; Percent complete: 34.4%; Average loss: 3.0789
Iteration: 1377; Percent complete: 34.4%; Average loss: 3.0483
Iteration: 1378; Percent complete: 34.4%; Average loss: 3.1769
Iteration: 1379; Percent complete: 34.5%; Average loss: 3.2365
Iteration: 1380; Percent complete: 34.5%; Average loss: 3.0947
Iteration: 1381; Percent complete: 34.5%; Average loss: 3.3714
Iteration: 1382; Percent complete: 34.5%; Average loss: 3.1509
Iteration: 1383; Percent complete: 34.6%; Average loss: 3.3681
Iteration: 1384; Percent complete: 34.6%; Average loss: 3.2461
Iteration: 1385; Percent complete: 34.6%; Average loss: 3.2975
Iteration: 1386; Percent complete: 34.6%; Average loss: 3.5677
Iteration: 1387; Percent complete: 34.7%; Average loss: 3.4362
Iteration: 1388; Percent complete: 34.7%; Average loss: 3.3636
Iteration: 1389; Percent complete: 34.7%; Average loss: 3.1265
Iteration: 1390; Percent complete: 34.8%; Average loss: 3.2586
Iteration: 1391; Percent complete: 34.8%; Average loss: 3.3536
Iteration: 1392; Percent complete: 34.8%; Average loss: 3.5429
Iteration: 1393; Percent complete: 34.8%; Average loss: 3.2683
Iteration: 1394; Percent complete: 34.8%; Average loss: 3.4517
Iteration: 1395; Percent complete: 34.9%; Average loss: 3.3189
Iteration: 1396; Percent complete: 34.9%; Average loss: 3.1509
Iteration: 1397; Percent complete: 34.9%; Average loss: 3.5154
Iteration: 1398; Percent complete: 34.9%; Average loss: 3.1526
Iteration: 1399; Percent complete: 35.0%; Average loss: 3.4440
Iteration: 1400; Percent complete: 35.0%; Average loss: 3.3547
Iteration: 1401; Percent complete: 35.0%; Average loss: 3.4180
Iteration: 1402; Percent complete: 35.0%; Average loss: 3.1032
Iteration: 1403; Percent complete: 35.1%; Average loss: 3.3294
Iteration: 1404; Percent complete: 35.1%; Average loss: 3.3398
Iteration: 1405; Percent complete: 35.1%; Average loss: 3.0976
Iteration: 1406; Percent complete: 35.1%; Average loss: 3.6106
Iteration: 1407; Percent complete: 35.2%; Average loss: 3.3672
Iteration: 1408; Percent complete: 35.2%; Average loss: 3.4063
Iteration: 1409; Percent complete: 35.2%; Average loss: 3.1280
Iteration: 1410; Percent complete: 35.2%; Average loss: 3.5229
Iteration: 1411; Percent complete: 35.3%; Average loss: 3.5220
Iteration: 1412; Percent complete: 35.3%; Average loss: 3.3527
Iteration: 1413; Percent complete: 35.3%; Average loss: 3.9073
Iteration: 1414; Percent complete: 35.4%; Average loss: 3.4397
Iteration: 1415; Percent complete: 35.4%; Average loss: 3.3809
Iteration: 1416; Percent complete: 35.4%; Average loss: 3.3566
Iteration: 1417; Percent complete: 35.4%; Average loss: 3.4912
Iteration: 1418; Percent complete: 35.4%; Average loss: 3.4030
Iteration: 1419; Percent complete: 35.5%; Average loss: 3.4393
Iteration: 1420; Percent complete: 35.5%; Average loss: 3.4258
Iteration: 1421; Percent complete: 35.5%; Average loss: 3.5057
Iteration: 1422; Percent complete: 35.5%; Average loss: 3.2836
Iteration: 1423; Percent complete: 35.6%; Average loss: 3.4137
Iteration: 1424; Percent complete: 35.6%; Average loss: 3.5620
Iteration: 1425; Percent complete: 35.6%; Average loss: 3.6315
Iteration: 1426; Percent complete: 35.6%; Average loss: 3.3165
Iteration: 1427; Percent complete: 35.7%; Average loss: 3.1931
Iteration: 1428; Percent complete: 35.7%; Average loss: 3.2500
Iteration: 1429; Percent complete: 35.7%; Average loss: 3.2067
Iteration: 1430; Percent complete: 35.8%; Average loss: 3.3352
Iteration: 1431; Percent complete: 35.8%; Average loss: 3.2734
Iteration: 1432; Percent complete: 35.8%; Average loss: 3.2733
Iteration: 1433; Percent complete: 35.8%; Average loss: 2.9451
Iteration: 1434; Percent complete: 35.9%; Average loss: 3.4999
Iteration: 1435; Percent complete: 35.9%; Average loss: 3.2150
Iteration: 1436; Percent complete: 35.9%; Average loss: 3.3119
Iteration: 1437; Percent complete: 35.9%; Average loss: 3.3006
Iteration: 1438; Percent complete: 35.9%; Average loss: 3.3489
Iteration: 1439; Percent complete: 36.0%; Average loss: 3.3044
Iteration: 1440; Percent complete: 36.0%; Average loss: 3.4558
Iteration: 1441; Percent complete: 36.0%; Average loss: 3.4272
Iteration: 1442; Percent complete: 36.0%; Average loss: 3.3097
Iteration: 1443; Percent complete: 36.1%; Average loss: 3.3585
Iteration: 1444; Percent complete: 36.1%; Average loss: 3.3343
Iteration: 1445; Percent complete: 36.1%; Average loss: 3.2336
Iteration: 1446; Percent complete: 36.1%; Average loss: 3.5981
Iteration: 1447; Percent complete: 36.2%; Average loss: 3.3532
Iteration: 1448; Percent complete: 36.2%; Average loss: 3.2548
Iteration: 1449; Percent complete: 36.2%; Average loss: 3.2176
Iteration: 1450; Percent complete: 36.2%; Average loss: 3.1945
Iteration: 1451; Percent complete: 36.3%; Average loss: 3.5250
Iteration: 1452; Percent complete: 36.3%; Average loss: 3.3887
Iteration: 1453; Percent complete: 36.3%; Average loss: 3.5631
Iteration: 1454; Percent complete: 36.4%; Average loss: 3.3309
Iteration: 1455; Percent complete: 36.4%; Average loss: 3.4097
Iteration: 1456; Percent complete: 36.4%; Average loss: 3.3122
Iteration: 1457; Percent complete: 36.4%; Average loss: 3.2084
Iteration: 1458; Percent complete: 36.4%; Average loss: 3.3284
Iteration: 1459; Percent complete: 36.5%; Average loss: 3.2869
Iteration: 1460; Percent complete: 36.5%; Average loss: 3.5638
Iteration: 1461; Percent complete: 36.5%; Average loss: 3.5186
Iteration: 1462; Percent complete: 36.5%; Average loss: 3.0271
Iteration: 1463; Percent complete: 36.6%; Average loss: 3.2105
Iteration: 1464; Percent complete: 36.6%; Average loss: 3.2643
Iteration: 1465; Percent complete: 36.6%; Average loss: 3.1468
Iteration: 1466; Percent complete: 36.6%; Average loss: 3.3700
Iteration: 1467; Percent complete: 36.7%; Average loss: 3.3995
Iteration: 1468; Percent complete: 36.7%; Average loss: 3.1837
Iteration: 1469; Percent complete: 36.7%; Average loss: 3.2336
Iteration: 1470; Percent complete: 36.8%; Average loss: 3.1865
Iteration: 1471; Percent complete: 36.8%; Average loss: 3.3644
Iteration: 1472; Percent complete: 36.8%; Average loss: 3.1657
Iteration: 1473; Percent complete: 36.8%; Average loss: 3.2460
Iteration: 1474; Percent complete: 36.9%; Average loss: 3.3190
Iteration: 1475; Percent complete: 36.9%; Average loss: 3.2306
Iteration: 1476; Percent complete: 36.9%; Average loss: 3.1904
Iteration: 1477; Percent complete: 36.9%; Average loss: 3.2714
Iteration: 1478; Percent complete: 37.0%; Average loss: 3.2445
Iteration: 1479; Percent complete: 37.0%; Average loss: 3.4353
Iteration: 1480; Percent complete: 37.0%; Average loss: 3.2513
Iteration: 1481; Percent complete: 37.0%; Average loss: 3.2545
Iteration: 1482; Percent complete: 37.0%; Average loss: 3.3194
Iteration: 1483; Percent complete: 37.1%; Average loss: 3.3970
Iteration: 1484; Percent complete: 37.1%; Average loss: 3.1244
Iteration: 1485; Percent complete: 37.1%; Average loss: 3.1398
Iteration: 1486; Percent complete: 37.1%; Average loss: 3.3114
Iteration: 1487; Percent complete: 37.2%; Average loss: 3.2133
Iteration: 1488; Percent complete: 37.2%; Average loss: 3.3688
Iteration: 1489; Percent complete: 37.2%; Average loss: 3.0983
Iteration: 1490; Percent complete: 37.2%; Average loss: 3.3356
Iteration: 1491; Percent complete: 37.3%; Average loss: 3.6513
Iteration: 1492; Percent complete: 37.3%; Average loss: 3.1293
Iteration: 1493; Percent complete: 37.3%; Average loss: 3.4139
Iteration: 1494; Percent complete: 37.4%; Average loss: 3.6409
Iteration: 1495; Percent complete: 37.4%; Average loss: 3.3269
Iteration: 1496; Percent complete: 37.4%; Average loss: 3.3471
Iteration: 1497; Percent complete: 37.4%; Average loss: 3.2268
Iteration: 1498; Percent complete: 37.5%; Average loss: 3.1756
Iteration: 1499; Percent complete: 37.5%; Average loss: 3.2516
Iteration: 1500; Percent complete: 37.5%; Average loss: 3.2568
Iteration: 1501; Percent complete: 37.5%; Average loss: 3.2801
Iteration: 1502; Percent complete: 37.5%; Average loss: 3.4952
Iteration: 1503; Percent complete: 37.6%; Average loss: 3.4741
Iteration: 1504; Percent complete: 37.6%; Average loss: 3.0353
Iteration: 1505; Percent complete: 37.6%; Average loss: 3.3832
Iteration: 1506; Percent complete: 37.6%; Average loss: 3.2272
Iteration: 1507; Percent complete: 37.7%; Average loss: 3.2370
Iteration: 1508; Percent complete: 37.7%; Average loss: 3.2718
Iteration: 1509; Percent complete: 37.7%; Average loss: 3.5800
Iteration: 1510; Percent complete: 37.8%; Average loss: 3.3085
Iteration: 1511; Percent complete: 37.8%; Average loss: 3.4347
Iteration: 1512; Percent complete: 37.8%; Average loss: 3.0440
Iteration: 1513; Percent complete: 37.8%; Average loss: 3.3564
Iteration: 1514; Percent complete: 37.9%; Average loss: 3.2163
Iteration: 1515; Percent complete: 37.9%; Average loss: 3.2165
Iteration: 1516; Percent complete: 37.9%; Average loss: 3.1029
Iteration: 1517; Percent complete: 37.9%; Average loss: 3.4130
Iteration: 1518; Percent complete: 38.0%; Average loss: 3.1231
Iteration: 1519; Percent complete: 38.0%; Average loss: 3.5129
Iteration: 1520; Percent complete: 38.0%; Average loss: 3.3033
Iteration: 1521; Percent complete: 38.0%; Average loss: 3.5067
Iteration: 1522; Percent complete: 38.0%; Average loss: 3.1419
Iteration: 1523; Percent complete: 38.1%; Average loss: 3.2225
Iteration: 1524; Percent complete: 38.1%; Average loss: 3.2686
Iteration: 1525; Percent complete: 38.1%; Average loss: 3.2186
Iteration: 1526; Percent complete: 38.1%; Average loss: 3.2728
Iteration: 1527; Percent complete: 38.2%; Average loss: 3.3566
Iteration: 1528; Percent complete: 38.2%; Average loss: 3.3734
Iteration: 1529; Percent complete: 38.2%; Average loss: 3.1990
Iteration: 1530; Percent complete: 38.2%; Average loss: 3.4845
Iteration: 1531; Percent complete: 38.3%; Average loss: 3.2765
Iteration: 1532; Percent complete: 38.3%; Average loss: 3.4769
Iteration: 1533; Percent complete: 38.3%; Average loss: 3.3794
Iteration: 1534; Percent complete: 38.4%; Average loss: 3.1958
Iteration: 1535; Percent complete: 38.4%; Average loss: 3.2752
Iteration: 1536; Percent complete: 38.4%; Average loss: 3.0196
Iteration: 1537; Percent complete: 38.4%; Average loss: 3.2560
Iteration: 1538; Percent complete: 38.5%; Average loss: 3.0382
Iteration: 1539; Percent complete: 38.5%; Average loss: 3.3225
Iteration: 1540; Percent complete: 38.5%; Average loss: 3.3428
Iteration: 1541; Percent complete: 38.5%; Average loss: 3.4253
Iteration: 1542; Percent complete: 38.6%; Average loss: 3.1649
Iteration: 1543; Percent complete: 38.6%; Average loss: 3.1003
Iteration: 1544; Percent complete: 38.6%; Average loss: 3.2931
Iteration: 1545; Percent complete: 38.6%; Average loss: 3.1268
Iteration: 1546; Percent complete: 38.6%; Average loss: 3.3557
Iteration: 1547; Percent complete: 38.7%; Average loss: 3.4115
Iteration: 1548; Percent complete: 38.7%; Average loss: 3.3696
Iteration: 1549; Percent complete: 38.7%; Average loss: 3.2793
Iteration: 1550; Percent complete: 38.8%; Average loss: 3.2967
Iteration: 1551; Percent complete: 38.8%; Average loss: 3.0511
Iteration: 1552; Percent complete: 38.8%; Average loss: 3.3372
Iteration: 1553; Percent complete: 38.8%; Average loss: 3.3054
Iteration: 1554; Percent complete: 38.9%; Average loss: 3.3760
Iteration: 1555; Percent complete: 38.9%; Average loss: 3.1250
Iteration: 1556; Percent complete: 38.9%; Average loss: 3.3258
Iteration: 1557; Percent complete: 38.9%; Average loss: 3.3403
Iteration: 1558; Percent complete: 39.0%; Average loss: 3.0275
Iteration: 1559; Percent complete: 39.0%; Average loss: 3.2378
Iteration: 1560; Percent complete: 39.0%; Average loss: 3.1499
Iteration: 1561; Percent complete: 39.0%; Average loss: 3.3168
Iteration: 1562; Percent complete: 39.1%; Average loss: 3.1861
Iteration: 1563; Percent complete: 39.1%; Average loss: 3.3154
Iteration: 1564; Percent complete: 39.1%; Average loss: 3.1832
Iteration: 1565; Percent complete: 39.1%; Average loss: 3.7764
Iteration: 1566; Percent complete: 39.1%; Average loss: 3.2535
Iteration: 1567; Percent complete: 39.2%; Average loss: 3.4194
Iteration: 1568; Percent complete: 39.2%; Average loss: 3.0311
Iteration: 1569; Percent complete: 39.2%; Average loss: 3.3320
Iteration: 1570; Percent complete: 39.2%; Average loss: 3.3433
Iteration: 1571; Percent complete: 39.3%; Average loss: 3.1202
Iteration: 1572; Percent complete: 39.3%; Average loss: 3.5132
Iteration: 1573; Percent complete: 39.3%; Average loss: 3.2124
Iteration: 1574; Percent complete: 39.4%; Average loss: 3.2673
Iteration: 1575; Percent complete: 39.4%; Average loss: 3.2659
Iteration: 1576; Percent complete: 39.4%; Average loss: 3.4357
Iteration: 1577; Percent complete: 39.4%; Average loss: 3.4183
Iteration: 1578; Percent complete: 39.5%; Average loss: 2.9766
Iteration: 1579; Percent complete: 39.5%; Average loss: 3.4478
Iteration: 1580; Percent complete: 39.5%; Average loss: 3.3334
Iteration: 1581; Percent complete: 39.5%; Average loss: 3.5449
Iteration: 1582; Percent complete: 39.6%; Average loss: 3.3935
Iteration: 1583; Percent complete: 39.6%; Average loss: 3.2877
Iteration: 1584; Percent complete: 39.6%; Average loss: 3.1313
Iteration: 1585; Percent complete: 39.6%; Average loss: 3.0282
Iteration: 1586; Percent complete: 39.6%; Average loss: 3.3057
Iteration: 1587; Percent complete: 39.7%; Average loss: 2.8991
Iteration: 1588; Percent complete: 39.7%; Average loss: 3.2079
Iteration: 1589; Percent complete: 39.7%; Average loss: 3.2824
Iteration: 1590; Percent complete: 39.8%; Average loss: 3.2401
Iteration: 1591; Percent complete: 39.8%; Average loss: 3.1440
Iteration: 1592; Percent complete: 39.8%; Average loss: 3.2053
Iteration: 1593; Percent complete: 39.8%; Average loss: 3.2176
Iteration: 1594; Percent complete: 39.9%; Average loss: 3.3350
Iteration: 1595; Percent complete: 39.9%; Average loss: 3.3012
Iteration: 1596; Percent complete: 39.9%; Average loss: 3.3228
Iteration: 1597; Percent complete: 39.9%; Average loss: 3.3582
Iteration: 1598; Percent complete: 40.0%; Average loss: 3.2249
Iteration: 1599; Percent complete: 40.0%; Average loss: 3.1640
Iteration: 1600; Percent complete: 40.0%; Average loss: 3.4582
Iteration: 1601; Percent complete: 40.0%; Average loss: 3.2015
Iteration: 1602; Percent complete: 40.1%; Average loss: 3.0345
Iteration: 1603; Percent complete: 40.1%; Average loss: 3.1330
Iteration: 1604; Percent complete: 40.1%; Average loss: 3.3478
Iteration: 1605; Percent complete: 40.1%; Average loss: 3.5680
Iteration: 1606; Percent complete: 40.2%; Average loss: 3.3133
Iteration: 1607; Percent complete: 40.2%; Average loss: 3.3209
Iteration: 1608; Percent complete: 40.2%; Average loss: 3.1625
Iteration: 1609; Percent complete: 40.2%; Average loss: 3.0762
Iteration: 1610; Percent complete: 40.2%; Average loss: 3.2251
Iteration: 1611; Percent complete: 40.3%; Average loss: 3.1536
Iteration: 1612; Percent complete: 40.3%; Average loss: 3.2789
Iteration: 1613; Percent complete: 40.3%; Average loss: 2.9994
Iteration: 1614; Percent complete: 40.4%; Average loss: 3.2038
Iteration: 1615; Percent complete: 40.4%; Average loss: 3.4911
Iteration: 1616; Percent complete: 40.4%; Average loss: 3.5345
Iteration: 1617; Percent complete: 40.4%; Average loss: 3.5364
Iteration: 1618; Percent complete: 40.5%; Average loss: 3.2144
Iteration: 1619; Percent complete: 40.5%; Average loss: 3.1770
Iteration: 1620; Percent complete: 40.5%; Average loss: 3.2872
Iteration: 1621; Percent complete: 40.5%; Average loss: 3.2457
Iteration: 1622; Percent complete: 40.6%; Average loss: 3.1291
Iteration: 1623; Percent complete: 40.6%; Average loss: 3.3680
Iteration: 1624; Percent complete: 40.6%; Average loss: 3.2276
Iteration: 1625; Percent complete: 40.6%; Average loss: 3.2433
Iteration: 1626; Percent complete: 40.6%; Average loss: 3.3993
Iteration: 1627; Percent complete: 40.7%; Average loss: 3.4206
Iteration: 1628; Percent complete: 40.7%; Average loss: 3.2838
Iteration: 1629; Percent complete: 40.7%; Average loss: 3.4540
Iteration: 1630; Percent complete: 40.8%; Average loss: 3.4897
Iteration: 1631; Percent complete: 40.8%; Average loss: 3.4028
Iteration: 1632; Percent complete: 40.8%; Average loss: 3.1680
Iteration: 1633; Percent complete: 40.8%; Average loss: 3.0499
Iteration: 1634; Percent complete: 40.8%; Average loss: 3.4677
Iteration: 1635; Percent complete: 40.9%; Average loss: 3.0731
Iteration: 1636; Percent complete: 40.9%; Average loss: 3.4609
Iteration: 1637; Percent complete: 40.9%; Average loss: 3.2362
Iteration: 1638; Percent complete: 40.9%; Average loss: 3.1794
Iteration: 1639; Percent complete: 41.0%; Average loss: 3.3985
Iteration: 1640; Percent complete: 41.0%; Average loss: 3.2838
Iteration: 1641; Percent complete: 41.0%; Average loss: 3.1574
Iteration: 1642; Percent complete: 41.0%; Average loss: 3.3043
Iteration: 1643; Percent complete: 41.1%; Average loss: 2.9130
Iteration: 1644; Percent complete: 41.1%; Average loss: 3.5688
Iteration: 1645; Percent complete: 41.1%; Average loss: 3.3602
Iteration: 1646; Percent complete: 41.1%; Average loss: 3.2957
Iteration: 1647; Percent complete: 41.2%; Average loss: 3.0853
Iteration: 1648; Percent complete: 41.2%; Average loss: 2.9617
Iteration: 1649; Percent complete: 41.2%; Average loss: 3.1638
Iteration: 1650; Percent complete: 41.2%; Average loss: 2.8677
Iteration: 1651; Percent complete: 41.3%; Average loss: 3.3997
Iteration: 1652; Percent complete: 41.3%; Average loss: 3.3317
Iteration: 1653; Percent complete: 41.3%; Average loss: 3.5168
Iteration: 1654; Percent complete: 41.3%; Average loss: 3.1784
Iteration: 1655; Percent complete: 41.4%; Average loss: 3.0547
Iteration: 1656; Percent complete: 41.4%; Average loss: 3.2751
Iteration: 1657; Percent complete: 41.4%; Average loss: 3.3176
Iteration: 1658; Percent complete: 41.4%; Average loss: 3.4018
Iteration: 1659; Percent complete: 41.5%; Average loss: 3.3865
Iteration: 1660; Percent complete: 41.5%; Average loss: 3.1114
Iteration: 1661; Percent complete: 41.5%; Average loss: 3.2355
Iteration: 1662; Percent complete: 41.5%; Average loss: 3.1397
Iteration: 1663; Percent complete: 41.6%; Average loss: 3.4410
Iteration: 1664; Percent complete: 41.6%; Average loss: 3.2501
Iteration: 1665; Percent complete: 41.6%; Average loss: 3.2542
Iteration: 1666; Percent complete: 41.6%; Average loss: 3.2657
Iteration: 1667; Percent complete: 41.7%; Average loss: 3.2070
Iteration: 1668; Percent complete: 41.7%; Average loss: 3.3273
Iteration: 1669; Percent complete: 41.7%; Average loss: 3.4070
Iteration: 1670; Percent complete: 41.8%; Average loss: 3.0603
Iteration: 1671; Percent complete: 41.8%; Average loss: 3.4680
Iteration: 1672; Percent complete: 41.8%; Average loss: 3.1586
Iteration: 1673; Percent complete: 41.8%; Average loss: 3.1091
Iteration: 1674; Percent complete: 41.9%; Average loss: 3.2253
Iteration: 1675; Percent complete: 41.9%; Average loss: 3.2172
Iteration: 1676; Percent complete: 41.9%; Average loss: 3.2940
Iteration: 1677; Percent complete: 41.9%; Average loss: 3.1674
Iteration: 1678; Percent complete: 41.9%; Average loss: 3.2712
Iteration: 1679; Percent complete: 42.0%; Average loss: 2.9452
Iteration: 1680; Percent complete: 42.0%; Average loss: 3.3078
Iteration: 1681; Percent complete: 42.0%; Average loss: 3.2255
Iteration: 1682; Percent complete: 42.0%; Average loss: 3.1308
Iteration: 1683; Percent complete: 42.1%; Average loss: 3.2488
Iteration: 1684; Percent complete: 42.1%; Average loss: 3.3458
Iteration: 1685; Percent complete: 42.1%; Average loss: 3.0961
Iteration: 1686; Percent complete: 42.1%; Average loss: 3.1434
Iteration: 1687; Percent complete: 42.2%; Average loss: 3.0582
Iteration: 1688; Percent complete: 42.2%; Average loss: 3.1460
Iteration: 1689; Percent complete: 42.2%; Average loss: 3.3418
Iteration: 1690; Percent complete: 42.2%; Average loss: 3.5222
Iteration: 1691; Percent complete: 42.3%; Average loss: 3.3845
Iteration: 1692; Percent complete: 42.3%; Average loss: 3.3781
Iteration: 1693; Percent complete: 42.3%; Average loss: 3.3575
Iteration: 1694; Percent complete: 42.4%; Average loss: 3.2190
Iteration: 1695; Percent complete: 42.4%; Average loss: 3.3196
Iteration: 1696; Percent complete: 42.4%; Average loss: 3.2568
Iteration: 1697; Percent complete: 42.4%; Average loss: 3.1706
Iteration: 1698; Percent complete: 42.4%; Average loss: 3.3029
Iteration: 1699; Percent complete: 42.5%; Average loss: 3.4567
Iteration: 1700; Percent complete: 42.5%; Average loss: 3.2121
Iteration: 1701; Percent complete: 42.5%; Average loss: 3.2313
Iteration: 1702; Percent complete: 42.5%; Average loss: 2.8777
Iteration: 1703; Percent complete: 42.6%; Average loss: 3.4613
Iteration: 1704; Percent complete: 42.6%; Average loss: 3.3111
Iteration: 1705; Percent complete: 42.6%; Average loss: 3.2275
Iteration: 1706; Percent complete: 42.6%; Average loss: 3.2215
Iteration: 1707; Percent complete: 42.7%; Average loss: 2.9867
Iteration: 1708; Percent complete: 42.7%; Average loss: 3.5364
Iteration: 1709; Percent complete: 42.7%; Average loss: 3.4295
Iteration: 1710; Percent complete: 42.8%; Average loss: 3.4621
Iteration: 1711; Percent complete: 42.8%; Average loss: 3.3981
Iteration: 1712; Percent complete: 42.8%; Average loss: 3.1920
Iteration: 1713; Percent complete: 42.8%; Average loss: 3.2638
Iteration: 1714; Percent complete: 42.9%; Average loss: 3.3479
Iteration: 1715; Percent complete: 42.9%; Average loss: 3.3726
Iteration: 1716; Percent complete: 42.9%; Average loss: 3.2799
Iteration: 1717; Percent complete: 42.9%; Average loss: 3.1669
Iteration: 1718; Percent complete: 43.0%; Average loss: 3.4901
Iteration: 1719; Percent complete: 43.0%; Average loss: 3.3777
Iteration: 1720; Percent complete: 43.0%; Average loss: 3.3799
Iteration: 1721; Percent complete: 43.0%; Average loss: 3.3214
Iteration: 1722; Percent complete: 43.0%; Average loss: 3.1871
Iteration: 1723; Percent complete: 43.1%; Average loss: 3.3127
Iteration: 1724; Percent complete: 43.1%; Average loss: 3.3167
Iteration: 1725; Percent complete: 43.1%; Average loss: 3.2049
Iteration: 1726; Percent complete: 43.1%; Average loss: 3.2840
Iteration: 1727; Percent complete: 43.2%; Average loss: 3.2602
Iteration: 1728; Percent complete: 43.2%; Average loss: 3.2959
Iteration: 1729; Percent complete: 43.2%; Average loss: 3.3205
Iteration: 1730; Percent complete: 43.2%; Average loss: 3.0056
Iteration: 1731; Percent complete: 43.3%; Average loss: 3.2097
Iteration: 1732; Percent complete: 43.3%; Average loss: 3.1234
Iteration: 1733; Percent complete: 43.3%; Average loss: 3.2737
Iteration: 1734; Percent complete: 43.4%; Average loss: 2.9732
Iteration: 1735; Percent complete: 43.4%; Average loss: 3.4265
Iteration: 1736; Percent complete: 43.4%; Average loss: 3.2408
Iteration: 1737; Percent complete: 43.4%; Average loss: 3.1449
Iteration: 1738; Percent complete: 43.5%; Average loss: 3.3260
Iteration: 1739; Percent complete: 43.5%; Average loss: 3.4004
Iteration: 1740; Percent complete: 43.5%; Average loss: 3.0022
Iteration: 1741; Percent complete: 43.5%; Average loss: 3.4770
Iteration: 1742; Percent complete: 43.5%; Average loss: 3.6169
Iteration: 1743; Percent complete: 43.6%; Average loss: 3.2265
Iteration: 1744; Percent complete: 43.6%; Average loss: 3.1474
Iteration: 1745; Percent complete: 43.6%; Average loss: 3.1423
Iteration: 1746; Percent complete: 43.6%; Average loss: 3.2367
Iteration: 1747; Percent complete: 43.7%; Average loss: 3.4137
Iteration: 1748; Percent complete: 43.7%; Average loss: 3.3387
Iteration: 1749; Percent complete: 43.7%; Average loss: 3.3435
Iteration: 1750; Percent complete: 43.8%; Average loss: 3.0660
Iteration: 1751; Percent complete: 43.8%; Average loss: 3.0963
Iteration: 1752; Percent complete: 43.8%; Average loss: 3.1774
Iteration: 1753; Percent complete: 43.8%; Average loss: 3.1688
Iteration: 1754; Percent complete: 43.9%; Average loss: 3.2971
Iteration: 1755; Percent complete: 43.9%; Average loss: 3.0696
Iteration: 1756; Percent complete: 43.9%; Average loss: 3.4080
Iteration: 1757; Percent complete: 43.9%; Average loss: 3.1634
Iteration: 1758; Percent complete: 44.0%; Average loss: 3.1090
Iteration: 1759; Percent complete: 44.0%; Average loss: 3.4121
Iteration: 1760; Percent complete: 44.0%; Average loss: 3.4632
Iteration: 1761; Percent complete: 44.0%; Average loss: 3.1014
Iteration: 1762; Percent complete: 44.0%; Average loss: 3.0433
Iteration: 1763; Percent complete: 44.1%; Average loss: 2.9371
Iteration: 1764; Percent complete: 44.1%; Average loss: 3.2650
Iteration: 1765; Percent complete: 44.1%; Average loss: 3.4208
Iteration: 1766; Percent complete: 44.1%; Average loss: 3.3577
Iteration: 1767; Percent complete: 44.2%; Average loss: 3.2390
Iteration: 1768; Percent complete: 44.2%; Average loss: 3.3533
Iteration: 1769; Percent complete: 44.2%; Average loss: 3.0208
Iteration: 1770; Percent complete: 44.2%; Average loss: 3.4012
Iteration: 1771; Percent complete: 44.3%; Average loss: 3.2617
Iteration: 1772; Percent complete: 44.3%; Average loss: 3.0660
Iteration: 1773; Percent complete: 44.3%; Average loss: 3.7008
Iteration: 1774; Percent complete: 44.4%; Average loss: 3.1122
Iteration: 1775; Percent complete: 44.4%; Average loss: 3.3437
Iteration: 1776; Percent complete: 44.4%; Average loss: 3.0367
Iteration: 1777; Percent complete: 44.4%; Average loss: 3.4770
Iteration: 1778; Percent complete: 44.5%; Average loss: 3.1708
Iteration: 1779; Percent complete: 44.5%; Average loss: 2.8772
Iteration: 1780; Percent complete: 44.5%; Average loss: 3.0997
Iteration: 1781; Percent complete: 44.5%; Average loss: 3.2125
Iteration: 1782; Percent complete: 44.5%; Average loss: 3.2106
Iteration: 1783; Percent complete: 44.6%; Average loss: 3.2129
Iteration: 1784; Percent complete: 44.6%; Average loss: 3.2029
Iteration: 1785; Percent complete: 44.6%; Average loss: 3.0701
Iteration: 1786; Percent complete: 44.6%; Average loss: 3.0309
Iteration: 1787; Percent complete: 44.7%; Average loss: 3.3493
Iteration: 1788; Percent complete: 44.7%; Average loss: 2.9514
Iteration: 1789; Percent complete: 44.7%; Average loss: 3.1694
Iteration: 1790; Percent complete: 44.8%; Average loss: 3.2438
Iteration: 1791; Percent complete: 44.8%; Average loss: 3.3735
Iteration: 1792; Percent complete: 44.8%; Average loss: 3.0927
Iteration: 1793; Percent complete: 44.8%; Average loss: 3.1473
Iteration: 1794; Percent complete: 44.9%; Average loss: 3.1729
Iteration: 1795; Percent complete: 44.9%; Average loss: 3.5889
Iteration: 1796; Percent complete: 44.9%; Average loss: 3.0907
Iteration: 1797; Percent complete: 44.9%; Average loss: 3.1760
Iteration: 1798; Percent complete: 45.0%; Average loss: 3.3853
Iteration: 1799; Percent complete: 45.0%; Average loss: 3.2291
Iteration: 1800; Percent complete: 45.0%; Average loss: 3.2736
Iteration: 1801; Percent complete: 45.0%; Average loss: 3.1692
Iteration: 1802; Percent complete: 45.1%; Average loss: 3.1098
Iteration: 1803; Percent complete: 45.1%; Average loss: 3.1345
Iteration: 1804; Percent complete: 45.1%; Average loss: 3.2530
Iteration: 1805; Percent complete: 45.1%; Average loss: 3.1618
Iteration: 1806; Percent complete: 45.1%; Average loss: 3.2423
Iteration: 1807; Percent complete: 45.2%; Average loss: 3.2803
Iteration: 1808; Percent complete: 45.2%; Average loss: 3.3718
Iteration: 1809; Percent complete: 45.2%; Average loss: 3.3759
Iteration: 1810; Percent complete: 45.2%; Average loss: 3.4049
Iteration: 1811; Percent complete: 45.3%; Average loss: 3.1530
Iteration: 1812; Percent complete: 45.3%; Average loss: 3.2835
Iteration: 1813; Percent complete: 45.3%; Average loss: 3.1521
Iteration: 1814; Percent complete: 45.4%; Average loss: 3.1874
Iteration: 1815; Percent complete: 45.4%; Average loss: 3.1074
Iteration: 1816; Percent complete: 45.4%; Average loss: 3.4439
Iteration: 1817; Percent complete: 45.4%; Average loss: 3.0703
Iteration: 1818; Percent complete: 45.5%; Average loss: 3.0002
Iteration: 1819; Percent complete: 45.5%; Average loss: 3.2358
Iteration: 1820; Percent complete: 45.5%; Average loss: 3.1267
Iteration: 1821; Percent complete: 45.5%; Average loss: 3.3373
Iteration: 1822; Percent complete: 45.6%; Average loss: 3.2476
Iteration: 1823; Percent complete: 45.6%; Average loss: 3.2590
Iteration: 1824; Percent complete: 45.6%; Average loss: 3.2325
Iteration: 1825; Percent complete: 45.6%; Average loss: 3.1218
Iteration: 1826; Percent complete: 45.6%; Average loss: 3.5153
Iteration: 1827; Percent complete: 45.7%; Average loss: 3.3218
Iteration: 1828; Percent complete: 45.7%; Average loss: 3.1056
Iteration: 1829; Percent complete: 45.7%; Average loss: 3.1468
Iteration: 1830; Percent complete: 45.8%; Average loss: 3.2107
Iteration: 1831; Percent complete: 45.8%; Average loss: 3.0447
Iteration: 1832; Percent complete: 45.8%; Average loss: 3.1606
Iteration: 1833; Percent complete: 45.8%; Average loss: 3.1335
Iteration: 1834; Percent complete: 45.9%; Average loss: 3.3197
Iteration: 1835; Percent complete: 45.9%; Average loss: 3.3259
Iteration: 1836; Percent complete: 45.9%; Average loss: 3.3389
Iteration: 1837; Percent complete: 45.9%; Average loss: 3.0499
Iteration: 1838; Percent complete: 46.0%; Average loss: 3.1213
Iteration: 1839; Percent complete: 46.0%; Average loss: 3.0860
Iteration: 1840; Percent complete: 46.0%; Average loss: 3.3008
Iteration: 1841; Percent complete: 46.0%; Average loss: 3.2538
Iteration: 1842; Percent complete: 46.1%; Average loss: 3.2533
Iteration: 1843; Percent complete: 46.1%; Average loss: 3.0758
Iteration: 1844; Percent complete: 46.1%; Average loss: 3.1244
Iteration: 1845; Percent complete: 46.1%; Average loss: 3.2804
Iteration: 1846; Percent complete: 46.2%; Average loss: 3.2682
Iteration: 1847; Percent complete: 46.2%; Average loss: 3.1544
Iteration: 1848; Percent complete: 46.2%; Average loss: 3.1363
Iteration: 1849; Percent complete: 46.2%; Average loss: 3.0920
Iteration: 1850; Percent complete: 46.2%; Average loss: 3.2519
Iteration: 1851; Percent complete: 46.3%; Average loss: 3.0433
Iteration: 1852; Percent complete: 46.3%; Average loss: 3.1643
Iteration: 1853; Percent complete: 46.3%; Average loss: 3.3890
Iteration: 1854; Percent complete: 46.4%; Average loss: 3.2709
Iteration: 1855; Percent complete: 46.4%; Average loss: 3.3221
Iteration: 1856; Percent complete: 46.4%; Average loss: 3.2979
Iteration: 1857; Percent complete: 46.4%; Average loss: 3.0698
Iteration: 1858; Percent complete: 46.5%; Average loss: 3.2342
Iteration: 1859; Percent complete: 46.5%; Average loss: 3.2935
Iteration: 1860; Percent complete: 46.5%; Average loss: 3.3117
Iteration: 1861; Percent complete: 46.5%; Average loss: 3.0643
Iteration: 1862; Percent complete: 46.6%; Average loss: 3.3841
Iteration: 1863; Percent complete: 46.6%; Average loss: 3.3423
Iteration: 1864; Percent complete: 46.6%; Average loss: 3.2881
Iteration: 1865; Percent complete: 46.6%; Average loss: 3.1838
Iteration: 1866; Percent complete: 46.7%; Average loss: 3.2113
Iteration: 1867; Percent complete: 46.7%; Average loss: 3.1817
Iteration: 1868; Percent complete: 46.7%; Average loss: 3.3985
Iteration: 1869; Percent complete: 46.7%; Average loss: 3.3292
Iteration: 1870; Percent complete: 46.8%; Average loss: 3.3130
Iteration: 1871; Percent complete: 46.8%; Average loss: 3.3703
Iteration: 1872; Percent complete: 46.8%; Average loss: 2.9882
Iteration: 1873; Percent complete: 46.8%; Average loss: 3.1887
Iteration: 1874; Percent complete: 46.9%; Average loss: 3.3030
Iteration: 1875; Percent complete: 46.9%; Average loss: 3.1755
Iteration: 1876; Percent complete: 46.9%; Average loss: 3.2009
Iteration: 1877; Percent complete: 46.9%; Average loss: 3.2653
Iteration: 1878; Percent complete: 46.9%; Average loss: 3.3111
Iteration: 1879; Percent complete: 47.0%; Average loss: 3.3241
Iteration: 1880; Percent complete: 47.0%; Average loss: 3.1876
Iteration: 1881; Percent complete: 47.0%; Average loss: 3.5473
Iteration: 1882; Percent complete: 47.0%; Average loss: 3.1385
Iteration: 1883; Percent complete: 47.1%; Average loss: 3.2649
Iteration: 1884; Percent complete: 47.1%; Average loss: 3.1665
Iteration: 1885; Percent complete: 47.1%; Average loss: 3.1649
Iteration: 1886; Percent complete: 47.1%; Average loss: 2.9407
Iteration: 1887; Percent complete: 47.2%; Average loss: 3.3501
Iteration: 1888; Percent complete: 47.2%; Average loss: 3.0910
Iteration: 1889; Percent complete: 47.2%; Average loss: 3.4995
Iteration: 1890; Percent complete: 47.2%; Average loss: 3.4194
Iteration: 1891; Percent complete: 47.3%; Average loss: 2.9547
Iteration: 1892; Percent complete: 47.3%; Average loss: 3.2571
Iteration: 1893; Percent complete: 47.3%; Average loss: 3.1806
Iteration: 1894; Percent complete: 47.3%; Average loss: 3.2276
Iteration: 1895; Percent complete: 47.4%; Average loss: 3.2433
Iteration: 1896; Percent complete: 47.4%; Average loss: 3.2843
Iteration: 1897; Percent complete: 47.4%; Average loss: 3.1460
Iteration: 1898; Percent complete: 47.4%; Average loss: 3.2334
Iteration: 1899; Percent complete: 47.5%; Average loss: 3.2747
Iteration: 1900; Percent complete: 47.5%; Average loss: 3.1995
Iteration: 1901; Percent complete: 47.5%; Average loss: 3.0883
Iteration: 1902; Percent complete: 47.5%; Average loss: 3.1410
Iteration: 1903; Percent complete: 47.6%; Average loss: 3.1745
Iteration: 1904; Percent complete: 47.6%; Average loss: 3.2105
Iteration: 1905; Percent complete: 47.6%; Average loss: 3.2509
Iteration: 1906; Percent complete: 47.6%; Average loss: 3.4053
Iteration: 1907; Percent complete: 47.7%; Average loss: 3.1196
Iteration: 1908; Percent complete: 47.7%; Average loss: 3.3791
Iteration: 1909; Percent complete: 47.7%; Average loss: 3.0895
Iteration: 1910; Percent complete: 47.8%; Average loss: 3.1346
Iteration: 1911; Percent complete: 47.8%; Average loss: 3.2579
Iteration: 1912; Percent complete: 47.8%; Average loss: 3.1135
Iteration: 1913; Percent complete: 47.8%; Average loss: 3.3191
Iteration: 1914; Percent complete: 47.9%; Average loss: 3.2127
Iteration: 1915; Percent complete: 47.9%; Average loss: 3.3031
Iteration: 1916; Percent complete: 47.9%; Average loss: 3.1616
Iteration: 1917; Percent complete: 47.9%; Average loss: 2.9323
Iteration: 1918; Percent complete: 47.9%; Average loss: 3.0695
Iteration: 1919; Percent complete: 48.0%; Average loss: 3.2027
Iteration: 1920; Percent complete: 48.0%; Average loss: 3.3395
Iteration: 1921; Percent complete: 48.0%; Average loss: 3.1354
Iteration: 1922; Percent complete: 48.0%; Average loss: 3.1923
Iteration: 1923; Percent complete: 48.1%; Average loss: 3.2348
Iteration: 1924; Percent complete: 48.1%; Average loss: 2.9867
Iteration: 1925; Percent complete: 48.1%; Average loss: 3.1045
Iteration: 1926; Percent complete: 48.1%; Average loss: 3.0872
Iteration: 1927; Percent complete: 48.2%; Average loss: 2.8696
Iteration: 1928; Percent complete: 48.2%; Average loss: 3.2074
Iteration: 1929; Percent complete: 48.2%; Average loss: 3.1323
Iteration: 1930; Percent complete: 48.2%; Average loss: 3.0859
Iteration: 1931; Percent complete: 48.3%; Average loss: 3.1272
Iteration: 1932; Percent complete: 48.3%; Average loss: 2.9827
Iteration: 1933; Percent complete: 48.3%; Average loss: 3.2866
Iteration: 1934; Percent complete: 48.4%; Average loss: 3.2613
Iteration: 1935; Percent complete: 48.4%; Average loss: 3.1997
Iteration: 1936; Percent complete: 48.4%; Average loss: 3.1177
Iteration: 1937; Percent complete: 48.4%; Average loss: 3.2446
Iteration: 1938; Percent complete: 48.4%; Average loss: 3.1373
Iteration: 1939; Percent complete: 48.5%; Average loss: 3.0356
Iteration: 1940; Percent complete: 48.5%; Average loss: 3.2590
Iteration: 1941; Percent complete: 48.5%; Average loss: 3.2511
Iteration: 1942; Percent complete: 48.5%; Average loss: 3.1911
Iteration: 1943; Percent complete: 48.6%; Average loss: 2.9556
Iteration: 1944; Percent complete: 48.6%; Average loss: 3.1957
Iteration: 1945; Percent complete: 48.6%; Average loss: 3.0937
Iteration: 1946; Percent complete: 48.6%; Average loss: 3.2658
Iteration: 1947; Percent complete: 48.7%; Average loss: 3.1908
Iteration: 1948; Percent complete: 48.7%; Average loss: 3.2127
Iteration: 1949; Percent complete: 48.7%; Average loss: 3.3056
Iteration: 1950; Percent complete: 48.8%; Average loss: 3.4529
Iteration: 1951; Percent complete: 48.8%; Average loss: 3.0647
Iteration: 1952; Percent complete: 48.8%; Average loss: 3.0277
Iteration: 1953; Percent complete: 48.8%; Average loss: 3.4043
Iteration: 1954; Percent complete: 48.9%; Average loss: 3.3746
Iteration: 1955; Percent complete: 48.9%; Average loss: 3.1870
Iteration: 1956; Percent complete: 48.9%; Average loss: 3.3628
Iteration: 1957; Percent complete: 48.9%; Average loss: 3.2663
Iteration: 1958; Percent complete: 48.9%; Average loss: 3.3062
Iteration: 1959; Percent complete: 49.0%; Average loss: 3.3000
Iteration: 1960; Percent complete: 49.0%; Average loss: 3.2045
Iteration: 1961; Percent complete: 49.0%; Average loss: 3.2732
Iteration: 1962; Percent complete: 49.0%; Average loss: 3.1638
Iteration: 1963; Percent complete: 49.1%; Average loss: 3.5006
Iteration: 1964; Percent complete: 49.1%; Average loss: 3.1192
Iteration: 1965; Percent complete: 49.1%; Average loss: 3.1071
Iteration: 1966; Percent complete: 49.1%; Average loss: 3.0994
Iteration: 1967; Percent complete: 49.2%; Average loss: 3.0883
Iteration: 1968; Percent complete: 49.2%; Average loss: 3.1629
Iteration: 1969; Percent complete: 49.2%; Average loss: 3.0986
Iteration: 1970; Percent complete: 49.2%; Average loss: 2.9715
Iteration: 1971; Percent complete: 49.3%; Average loss: 3.3219
Iteration: 1972; Percent complete: 49.3%; Average loss: 3.1821
Iteration: 1973; Percent complete: 49.3%; Average loss: 3.2167
Iteration: 1974; Percent complete: 49.4%; Average loss: 3.0210
Iteration: 1975; Percent complete: 49.4%; Average loss: 3.3884
Iteration: 1976; Percent complete: 49.4%; Average loss: 3.2074
Iteration: 1977; Percent complete: 49.4%; Average loss: 2.8861
Iteration: 1978; Percent complete: 49.5%; Average loss: 3.0512
Iteration: 1979; Percent complete: 49.5%; Average loss: 2.9531
Iteration: 1980; Percent complete: 49.5%; Average loss: 3.1636
Iteration: 1981; Percent complete: 49.5%; Average loss: 3.1199
Iteration: 1982; Percent complete: 49.5%; Average loss: 3.1275
Iteration: 1983; Percent complete: 49.6%; Average loss: 2.9594
Iteration: 1984; Percent complete: 49.6%; Average loss: 3.1855
Iteration: 1985; Percent complete: 49.6%; Average loss: 3.2389
Iteration: 1986; Percent complete: 49.6%; Average loss: 3.2459
Iteration: 1987; Percent complete: 49.7%; Average loss: 3.1442
Iteration: 1988; Percent complete: 49.7%; Average loss: 3.2245
Iteration: 1989; Percent complete: 49.7%; Average loss: 3.2663
Iteration: 1990; Percent complete: 49.8%; Average loss: 3.2858
Iteration: 1991; Percent complete: 49.8%; Average loss: 2.8889
Iteration: 1992; Percent complete: 49.8%; Average loss: 2.9643
Iteration: 1993; Percent complete: 49.8%; Average loss: 3.2297
Iteration: 1994; Percent complete: 49.9%; Average loss: 3.0877
Iteration: 1995; Percent complete: 49.9%; Average loss: 2.8898
Iteration: 1996; Percent complete: 49.9%; Average loss: 3.2252
Iteration: 1997; Percent complete: 49.9%; Average loss: 3.1903
Iteration: 1998; Percent complete: 50.0%; Average loss: 3.1128
Iteration: 1999; Percent complete: 50.0%; Average loss: 3.0963
Iteration: 2000; Percent complete: 50.0%; Average loss: 3.0260
Iteration: 2001; Percent complete: 50.0%; Average loss: 3.4384
Iteration: 2002; Percent complete: 50.0%; Average loss: 3.0640
Iteration: 2003; Percent complete: 50.1%; Average loss: 3.1367
Iteration: 2004; Percent complete: 50.1%; Average loss: 3.0388
Iteration: 2005; Percent complete: 50.1%; Average loss: 3.2145
Iteration: 2006; Percent complete: 50.1%; Average loss: 3.1661
Iteration: 2007; Percent complete: 50.2%; Average loss: 3.0297
Iteration: 2008; Percent complete: 50.2%; Average loss: 3.0633
Iteration: 2009; Percent complete: 50.2%; Average loss: 2.9861
Iteration: 2010; Percent complete: 50.2%; Average loss: 3.0394
Iteration: 2011; Percent complete: 50.3%; Average loss: 3.4037
Iteration: 2012; Percent complete: 50.3%; Average loss: 2.5752
Iteration: 2013; Percent complete: 50.3%; Average loss: 3.1104
Iteration: 2014; Percent complete: 50.3%; Average loss: 3.0633
Iteration: 2015; Percent complete: 50.4%; Average loss: 3.0430
Iteration: 2016; Percent complete: 50.4%; Average loss: 3.2834
Iteration: 2017; Percent complete: 50.4%; Average loss: 3.1341
Iteration: 2018; Percent complete: 50.4%; Average loss: 3.1601
Iteration: 2019; Percent complete: 50.5%; Average loss: 2.8019
Iteration: 2020; Percent complete: 50.5%; Average loss: 3.1175
Iteration: 2021; Percent complete: 50.5%; Average loss: 3.0337
Iteration: 2022; Percent complete: 50.5%; Average loss: 3.1737
Iteration: 2023; Percent complete: 50.6%; Average loss: 3.0870
Iteration: 2024; Percent complete: 50.6%; Average loss: 3.1591
Iteration: 2025; Percent complete: 50.6%; Average loss: 3.2097
Iteration: 2026; Percent complete: 50.6%; Average loss: 3.1063
Iteration: 2027; Percent complete: 50.7%; Average loss: 3.2171
Iteration: 2028; Percent complete: 50.7%; Average loss: 3.0547
Iteration: 2029; Percent complete: 50.7%; Average loss: 3.3289
Iteration: 2030; Percent complete: 50.7%; Average loss: 3.3937
Iteration: 2031; Percent complete: 50.8%; Average loss: 3.3730
Iteration: 2032; Percent complete: 50.8%; Average loss: 2.8974
Iteration: 2033; Percent complete: 50.8%; Average loss: 3.1747
Iteration: 2034; Percent complete: 50.8%; Average loss: 3.1414
Iteration: 2035; Percent complete: 50.9%; Average loss: 3.1091
Iteration: 2036; Percent complete: 50.9%; Average loss: 3.3973
Iteration: 2037; Percent complete: 50.9%; Average loss: 3.1101
Iteration: 2038; Percent complete: 50.9%; Average loss: 3.1794
Iteration: 2039; Percent complete: 51.0%; Average loss: 3.1188
Iteration: 2040; Percent complete: 51.0%; Average loss: 3.1989
Iteration: 2041; Percent complete: 51.0%; Average loss: 3.0105
Iteration: 2042; Percent complete: 51.0%; Average loss: 3.2509
Iteration: 2043; Percent complete: 51.1%; Average loss: 3.1327
Iteration: 2044; Percent complete: 51.1%; Average loss: 3.1537
Iteration: 2045; Percent complete: 51.1%; Average loss: 2.9883
Iteration: 2046; Percent complete: 51.1%; Average loss: 3.0848
Iteration: 2047; Percent complete: 51.2%; Average loss: 3.2173
Iteration: 2048; Percent complete: 51.2%; Average loss: 3.0758
Iteration: 2049; Percent complete: 51.2%; Average loss: 2.8697
Iteration: 2050; Percent complete: 51.2%; Average loss: 3.3477
Iteration: 2051; Percent complete: 51.3%; Average loss: 3.1337
Iteration: 2052; Percent complete: 51.3%; Average loss: 3.5787
Iteration: 2053; Percent complete: 51.3%; Average loss: 3.2399
Iteration: 2054; Percent complete: 51.3%; Average loss: 3.2691
Iteration: 2055; Percent complete: 51.4%; Average loss: 3.1219
Iteration: 2056; Percent complete: 51.4%; Average loss: 3.1796
Iteration: 2057; Percent complete: 51.4%; Average loss: 3.2556
Iteration: 2058; Percent complete: 51.4%; Average loss: 2.9780
Iteration: 2059; Percent complete: 51.5%; Average loss: 3.3349
Iteration: 2060; Percent complete: 51.5%; Average loss: 3.1966
Iteration: 2061; Percent complete: 51.5%; Average loss: 3.1768
Iteration: 2062; Percent complete: 51.5%; Average loss: 3.1065
Iteration: 2063; Percent complete: 51.6%; Average loss: 3.2352
Iteration: 2064; Percent complete: 51.6%; Average loss: 3.0157
Iteration: 2065; Percent complete: 51.6%; Average loss: 3.1071
Iteration: 2066; Percent complete: 51.6%; Average loss: 2.9320
Iteration: 2067; Percent complete: 51.7%; Average loss: 3.1046
Iteration: 2068; Percent complete: 51.7%; Average loss: 3.1534
Iteration: 2069; Percent complete: 51.7%; Average loss: 2.8869
Iteration: 2070; Percent complete: 51.7%; Average loss: 3.2194
Iteration: 2071; Percent complete: 51.8%; Average loss: 3.3216
Iteration: 2072; Percent complete: 51.8%; Average loss: 3.0875
Iteration: 2073; Percent complete: 51.8%; Average loss: 3.1150
Iteration: 2074; Percent complete: 51.8%; Average loss: 3.0087
Iteration: 2075; Percent complete: 51.9%; Average loss: 2.7736
Iteration: 2076; Percent complete: 51.9%; Average loss: 3.2995
Iteration: 2077; Percent complete: 51.9%; Average loss: 3.3210
Iteration: 2078; Percent complete: 51.9%; Average loss: 3.2907
Iteration: 2079; Percent complete: 52.0%; Average loss: 3.4561
Iteration: 2080; Percent complete: 52.0%; Average loss: 3.3913
Iteration: 2081; Percent complete: 52.0%; Average loss: 3.0513
Iteration: 2082; Percent complete: 52.0%; Average loss: 3.1763
Iteration: 2083; Percent complete: 52.1%; Average loss: 2.7863
Iteration: 2084; Percent complete: 52.1%; Average loss: 3.2899
Iteration: 2085; Percent complete: 52.1%; Average loss: 3.1965
Iteration: 2086; Percent complete: 52.1%; Average loss: 3.2088
Iteration: 2087; Percent complete: 52.2%; Average loss: 2.9348
Iteration: 2088; Percent complete: 52.2%; Average loss: 3.3141
Iteration: 2089; Percent complete: 52.2%; Average loss: 3.3429
Iteration: 2090; Percent complete: 52.2%; Average loss: 3.2297
Iteration: 2091; Percent complete: 52.3%; Average loss: 3.2827
Iteration: 2092; Percent complete: 52.3%; Average loss: 3.2448
Iteration: 2093; Percent complete: 52.3%; Average loss: 2.9935
Iteration: 2094; Percent complete: 52.3%; Average loss: 3.2943
Iteration: 2095; Percent complete: 52.4%; Average loss: 3.0887
Iteration: 2096; Percent complete: 52.4%; Average loss: 3.0033
Iteration: 2097; Percent complete: 52.4%; Average loss: 3.0356
Iteration: 2098; Percent complete: 52.4%; Average loss: 3.1235
Iteration: 2099; Percent complete: 52.5%; Average loss: 3.2155
Iteration: 2100; Percent complete: 52.5%; Average loss: 2.8660
Iteration: 2101; Percent complete: 52.5%; Average loss: 2.9888
Iteration: 2102; Percent complete: 52.5%; Average loss: 3.0124
Iteration: 2103; Percent complete: 52.6%; Average loss: 3.3258
Iteration: 2104; Percent complete: 52.6%; Average loss: 3.4199
Iteration: 2105; Percent complete: 52.6%; Average loss: 3.2269
Iteration: 2106; Percent complete: 52.6%; Average loss: 3.3385
Iteration: 2107; Percent complete: 52.7%; Average loss: 3.0955
Iteration: 2108; Percent complete: 52.7%; Average loss: 3.1044
Iteration: 2109; Percent complete: 52.7%; Average loss: 3.0570
Iteration: 2110; Percent complete: 52.8%; Average loss: 3.1607
Iteration: 2111; Percent complete: 52.8%; Average loss: 3.0149
Iteration: 2112; Percent complete: 52.8%; Average loss: 2.9628
Iteration: 2113; Percent complete: 52.8%; Average loss: 3.1668
Iteration: 2114; Percent complete: 52.8%; Average loss: 3.4587
Iteration: 2115; Percent complete: 52.9%; Average loss: 3.1778
Iteration: 2116; Percent complete: 52.9%; Average loss: 2.8981
Iteration: 2117; Percent complete: 52.9%; Average loss: 3.2325
Iteration: 2118; Percent complete: 52.9%; Average loss: 3.0502
Iteration: 2119; Percent complete: 53.0%; Average loss: 3.0857
Iteration: 2120; Percent complete: 53.0%; Average loss: 3.2351
Iteration: 2121; Percent complete: 53.0%; Average loss: 3.1013
Iteration: 2122; Percent complete: 53.0%; Average loss: 3.4023
Iteration: 2123; Percent complete: 53.1%; Average loss: 3.3490
Iteration: 2124; Percent complete: 53.1%; Average loss: 3.3127
Iteration: 2125; Percent complete: 53.1%; Average loss: 3.0916
Iteration: 2126; Percent complete: 53.1%; Average loss: 3.1862
Iteration: 2127; Percent complete: 53.2%; Average loss: 3.1635
Iteration: 2128; Percent complete: 53.2%; Average loss: 3.2214
Iteration: 2129; Percent complete: 53.2%; Average loss: 2.8461
Iteration: 2130; Percent complete: 53.2%; Average loss: 2.9856
Iteration: 2131; Percent complete: 53.3%; Average loss: 3.3030
Iteration: 2132; Percent complete: 53.3%; Average loss: 3.2113
Iteration: 2133; Percent complete: 53.3%; Average loss: 2.7086
Iteration: 2134; Percent complete: 53.3%; Average loss: 3.2281
Iteration: 2135; Percent complete: 53.4%; Average loss: 3.0957
Iteration: 2136; Percent complete: 53.4%; Average loss: 3.1673
Iteration: 2137; Percent complete: 53.4%; Average loss: 3.1692
Iteration: 2138; Percent complete: 53.4%; Average loss: 3.0788
Iteration: 2139; Percent complete: 53.5%; Average loss: 2.9017
Iteration: 2140; Percent complete: 53.5%; Average loss: 3.1361
Iteration: 2141; Percent complete: 53.5%; Average loss: 3.0072
Iteration: 2142; Percent complete: 53.5%; Average loss: 3.0664
Iteration: 2143; Percent complete: 53.6%; Average loss: 3.0940
Iteration: 2144; Percent complete: 53.6%; Average loss: 3.3955
Iteration: 2145; Percent complete: 53.6%; Average loss: 3.2739
Iteration: 2146; Percent complete: 53.6%; Average loss: 2.9476
Iteration: 2147; Percent complete: 53.7%; Average loss: 3.0959
Iteration: 2148; Percent complete: 53.7%; Average loss: 3.2363
Iteration: 2149; Percent complete: 53.7%; Average loss: 3.1239
Iteration: 2150; Percent complete: 53.8%; Average loss: 2.7260
Iteration: 2151; Percent complete: 53.8%; Average loss: 3.1950
Iteration: 2152; Percent complete: 53.8%; Average loss: 3.1939
Iteration: 2153; Percent complete: 53.8%; Average loss: 3.0327
Iteration: 2154; Percent complete: 53.8%; Average loss: 3.0776
Iteration: 2155; Percent complete: 53.9%; Average loss: 3.1469
Iteration: 2156; Percent complete: 53.9%; Average loss: 3.2861
Iteration: 2157; Percent complete: 53.9%; Average loss: 3.4012
Iteration: 2158; Percent complete: 53.9%; Average loss: 3.0332
Iteration: 2159; Percent complete: 54.0%; Average loss: 3.3731
Iteration: 2160; Percent complete: 54.0%; Average loss: 3.2334
Iteration: 2161; Percent complete: 54.0%; Average loss: 3.2296
Iteration: 2162; Percent complete: 54.0%; Average loss: 3.1828
Iteration: 2163; Percent complete: 54.1%; Average loss: 3.1333
Iteration: 2164; Percent complete: 54.1%; Average loss: 3.1082
Iteration: 2165; Percent complete: 54.1%; Average loss: 3.2060
Iteration: 2166; Percent complete: 54.1%; Average loss: 3.1800
Iteration: 2167; Percent complete: 54.2%; Average loss: 3.1656
Iteration: 2168; Percent complete: 54.2%; Average loss: 2.9009
Iteration: 2169; Percent complete: 54.2%; Average loss: 2.8314
Iteration: 2170; Percent complete: 54.2%; Average loss: 3.1258
Iteration: 2171; Percent complete: 54.3%; Average loss: 2.8747
Iteration: 2172; Percent complete: 54.3%; Average loss: 3.0220
Iteration: 2173; Percent complete: 54.3%; Average loss: 2.9649
Iteration: 2174; Percent complete: 54.4%; Average loss: 3.0871
Iteration: 2175; Percent complete: 54.4%; Average loss: 3.0684
Iteration: 2176; Percent complete: 54.4%; Average loss: 2.9144
Iteration: 2177; Percent complete: 54.4%; Average loss: 3.1323
Iteration: 2178; Percent complete: 54.4%; Average loss: 2.9539
Iteration: 2179; Percent complete: 54.5%; Average loss: 2.9871
Iteration: 2180; Percent complete: 54.5%; Average loss: 3.1922
Iteration: 2181; Percent complete: 54.5%; Average loss: 3.0817
Iteration: 2182; Percent complete: 54.5%; Average loss: 3.2066
Iteration: 2183; Percent complete: 54.6%; Average loss: 3.2834
Iteration: 2184; Percent complete: 54.6%; Average loss: 3.0244
Iteration: 2185; Percent complete: 54.6%; Average loss: 3.2362
Iteration: 2186; Percent complete: 54.6%; Average loss: 3.1035
Iteration: 2187; Percent complete: 54.7%; Average loss: 2.9420
Iteration: 2188; Percent complete: 54.7%; Average loss: 3.1531
Iteration: 2189; Percent complete: 54.7%; Average loss: 3.1259
Iteration: 2190; Percent complete: 54.8%; Average loss: 3.1188
Iteration: 2191; Percent complete: 54.8%; Average loss: 3.3013
Iteration: 2192; Percent complete: 54.8%; Average loss: 3.2583
Iteration: 2193; Percent complete: 54.8%; Average loss: 3.3663
Iteration: 2194; Percent complete: 54.9%; Average loss: 2.9382
Iteration: 2195; Percent complete: 54.9%; Average loss: 3.1536
Iteration: 2196; Percent complete: 54.9%; Average loss: 3.1991
Iteration: 2197; Percent complete: 54.9%; Average loss: 3.1099
Iteration: 2198; Percent complete: 54.9%; Average loss: 3.2744
Iteration: 2199; Percent complete: 55.0%; Average loss: 3.2474
Iteration: 2200; Percent complete: 55.0%; Average loss: 3.1838
Iteration: 2201; Percent complete: 55.0%; Average loss: 3.1044
Iteration: 2202; Percent complete: 55.0%; Average loss: 3.1596
Iteration: 2203; Percent complete: 55.1%; Average loss: 2.8759
Iteration: 2204; Percent complete: 55.1%; Average loss: 3.0020
Iteration: 2205; Percent complete: 55.1%; Average loss: 3.2031
Iteration: 2206; Percent complete: 55.1%; Average loss: 3.2097
Iteration: 2207; Percent complete: 55.2%; Average loss: 3.1706
Iteration: 2208; Percent complete: 55.2%; Average loss: 3.3713
Iteration: 2209; Percent complete: 55.2%; Average loss: 3.2580
Iteration: 2210; Percent complete: 55.2%; Average loss: 3.1005
Iteration: 2211; Percent complete: 55.3%; Average loss: 3.2233
Iteration: 2212; Percent complete: 55.3%; Average loss: 3.0806
Iteration: 2213; Percent complete: 55.3%; Average loss: 3.0042
Iteration: 2214; Percent complete: 55.4%; Average loss: 3.2806
Iteration: 2215; Percent complete: 55.4%; Average loss: 3.0888
Iteration: 2216; Percent complete: 55.4%; Average loss: 3.3834
Iteration: 2217; Percent complete: 55.4%; Average loss: 3.1211
Iteration: 2218; Percent complete: 55.5%; Average loss: 3.2071
Iteration: 2219; Percent complete: 55.5%; Average loss: 3.2576
Iteration: 2220; Percent complete: 55.5%; Average loss: 2.6695
Iteration: 2221; Percent complete: 55.5%; Average loss: 3.1700
Iteration: 2222; Percent complete: 55.5%; Average loss: 3.0955
Iteration: 2223; Percent complete: 55.6%; Average loss: 3.1390
Iteration: 2224; Percent complete: 55.6%; Average loss: 3.2136
Iteration: 2225; Percent complete: 55.6%; Average loss: 3.0084
Iteration: 2226; Percent complete: 55.6%; Average loss: 2.9607
Iteration: 2227; Percent complete: 55.7%; Average loss: 3.2107
Iteration: 2228; Percent complete: 55.7%; Average loss: 3.3415
Iteration: 2229; Percent complete: 55.7%; Average loss: 3.1057
Iteration: 2230; Percent complete: 55.8%; Average loss: 3.0558
Iteration: 2231; Percent complete: 55.8%; Average loss: 3.1272
Iteration: 2232; Percent complete: 55.8%; Average loss: 2.9258
Iteration: 2233; Percent complete: 55.8%; Average loss: 3.0704
Iteration: 2234; Percent complete: 55.9%; Average loss: 2.8269
Iteration: 2235; Percent complete: 55.9%; Average loss: 3.2658
Iteration: 2236; Percent complete: 55.9%; Average loss: 3.2194
Iteration: 2237; Percent complete: 55.9%; Average loss: 2.9536
Iteration: 2238; Percent complete: 56.0%; Average loss: 3.1668
Iteration: 2239; Percent complete: 56.0%; Average loss: 3.1232
Iteration: 2240; Percent complete: 56.0%; Average loss: 3.2924
Iteration: 2241; Percent complete: 56.0%; Average loss: 3.0515
Iteration: 2242; Percent complete: 56.0%; Average loss: 3.3266
Iteration: 2243; Percent complete: 56.1%; Average loss: 2.9043
Iteration: 2244; Percent complete: 56.1%; Average loss: 2.9906
Iteration: 2245; Percent complete: 56.1%; Average loss: 3.0214
Iteration: 2246; Percent complete: 56.1%; Average loss: 3.1326
Iteration: 2247; Percent complete: 56.2%; Average loss: 2.8161
Iteration: 2248; Percent complete: 56.2%; Average loss: 2.9952
Iteration: 2249; Percent complete: 56.2%; Average loss: 2.9404
Iteration: 2250; Percent complete: 56.2%; Average loss: 3.2104
Iteration: 2251; Percent complete: 56.3%; Average loss: 3.0755
Iteration: 2252; Percent complete: 56.3%; Average loss: 3.1313
Iteration: 2253; Percent complete: 56.3%; Average loss: 2.9337
Iteration: 2254; Percent complete: 56.4%; Average loss: 3.0053
Iteration: 2255; Percent complete: 56.4%; Average loss: 3.1391
Iteration: 2256; Percent complete: 56.4%; Average loss: 3.0201
Iteration: 2257; Percent complete: 56.4%; Average loss: 3.0184
Iteration: 2258; Percent complete: 56.5%; Average loss: 3.1412
Iteration: 2259; Percent complete: 56.5%; Average loss: 3.0425
Iteration: 2260; Percent complete: 56.5%; Average loss: 3.2152
Iteration: 2261; Percent complete: 56.5%; Average loss: 2.7879
Iteration: 2262; Percent complete: 56.5%; Average loss: 3.0082
Iteration: 2263; Percent complete: 56.6%; Average loss: 3.2613
Iteration: 2264; Percent complete: 56.6%; Average loss: 3.4773
Iteration: 2265; Percent complete: 56.6%; Average loss: 3.1468
Iteration: 2266; Percent complete: 56.6%; Average loss: 3.2709
Iteration: 2267; Percent complete: 56.7%; Average loss: 2.9786
Iteration: 2268; Percent complete: 56.7%; Average loss: 3.2503
Iteration: 2269; Percent complete: 56.7%; Average loss: 2.9408
Iteration: 2270; Percent complete: 56.8%; Average loss: 2.9433
Iteration: 2271; Percent complete: 56.8%; Average loss: 3.3117
Iteration: 2272; Percent complete: 56.8%; Average loss: 3.1481
Iteration: 2273; Percent complete: 56.8%; Average loss: 2.8818
Iteration: 2274; Percent complete: 56.9%; Average loss: 3.2805
Iteration: 2275; Percent complete: 56.9%; Average loss: 2.5916
Iteration: 2276; Percent complete: 56.9%; Average loss: 3.1306
Iteration: 2277; Percent complete: 56.9%; Average loss: 3.1879
Iteration: 2278; Percent complete: 57.0%; Average loss: 3.0540
Iteration: 2279; Percent complete: 57.0%; Average loss: 3.0808
Iteration: 2280; Percent complete: 57.0%; Average loss: 3.1295
Iteration: 2281; Percent complete: 57.0%; Average loss: 3.0182
Iteration: 2282; Percent complete: 57.0%; Average loss: 3.1888
Iteration: 2283; Percent complete: 57.1%; Average loss: 2.9730
Iteration: 2284; Percent complete: 57.1%; Average loss: 2.9734
Iteration: 2285; Percent complete: 57.1%; Average loss: 3.2218
Iteration: 2286; Percent complete: 57.1%; Average loss: 3.2927
Iteration: 2287; Percent complete: 57.2%; Average loss: 3.0729
Iteration: 2288; Percent complete: 57.2%; Average loss: 3.2652
Iteration: 2289; Percent complete: 57.2%; Average loss: 3.0433
Iteration: 2290; Percent complete: 57.2%; Average loss: 3.1546
Iteration: 2291; Percent complete: 57.3%; Average loss: 3.0593
Iteration: 2292; Percent complete: 57.3%; Average loss: 3.1448
Iteration: 2293; Percent complete: 57.3%; Average loss: 2.8357
Iteration: 2294; Percent complete: 57.4%; Average loss: 3.1137
Iteration: 2295; Percent complete: 57.4%; Average loss: 3.2850
Iteration: 2296; Percent complete: 57.4%; Average loss: 3.0675
Iteration: 2297; Percent complete: 57.4%; Average loss: 3.3014
Iteration: 2298; Percent complete: 57.5%; Average loss: 3.1427
Iteration: 2299; Percent complete: 57.5%; Average loss: 3.1564
Iteration: 2300; Percent complete: 57.5%; Average loss: 2.8548
Iteration: 2301; Percent complete: 57.5%; Average loss: 3.0083
Iteration: 2302; Percent complete: 57.6%; Average loss: 3.0255
Iteration: 2303; Percent complete: 57.6%; Average loss: 3.0992
Iteration: 2304; Percent complete: 57.6%; Average loss: 3.2029
Iteration: 2305; Percent complete: 57.6%; Average loss: 3.0757
Iteration: 2306; Percent complete: 57.6%; Average loss: 3.0999
Iteration: 2307; Percent complete: 57.7%; Average loss: 3.0460
Iteration: 2308; Percent complete: 57.7%; Average loss: 3.1038
Iteration: 2309; Percent complete: 57.7%; Average loss: 3.3139
Iteration: 2310; Percent complete: 57.8%; Average loss: 3.0499
Iteration: 2311; Percent complete: 57.8%; Average loss: 2.9930
Iteration: 2312; Percent complete: 57.8%; Average loss: 2.9262
Iteration: 2313; Percent complete: 57.8%; Average loss: 3.1812
Iteration: 2314; Percent complete: 57.9%; Average loss: 3.1261
Iteration: 2315; Percent complete: 57.9%; Average loss: 3.2745
Iteration: 2316; Percent complete: 57.9%; Average loss: 3.2344
Iteration: 2317; Percent complete: 57.9%; Average loss: 3.0680
Iteration: 2318; Percent complete: 58.0%; Average loss: 2.7868
Iteration: 2319; Percent complete: 58.0%; Average loss: 3.2036
Iteration: 2320; Percent complete: 58.0%; Average loss: 3.0845
Iteration: 2321; Percent complete: 58.0%; Average loss: 2.9211
Iteration: 2322; Percent complete: 58.1%; Average loss: 2.9423
Iteration: 2323; Percent complete: 58.1%; Average loss: 3.0052
Iteration: 2324; Percent complete: 58.1%; Average loss: 3.1236
Iteration: 2325; Percent complete: 58.1%; Average loss: 3.0260
Iteration: 2326; Percent complete: 58.1%; Average loss: 3.2437
Iteration: 2327; Percent complete: 58.2%; Average loss: 3.1023
Iteration: 2328; Percent complete: 58.2%; Average loss: 3.0209
Iteration: 2329; Percent complete: 58.2%; Average loss: 3.1200
Iteration: 2330; Percent complete: 58.2%; Average loss: 2.9882
Iteration: 2331; Percent complete: 58.3%; Average loss: 2.8224
Iteration: 2332; Percent complete: 58.3%; Average loss: 3.0919
Iteration: 2333; Percent complete: 58.3%; Average loss: 3.0649
Iteration: 2334; Percent complete: 58.4%; Average loss: 2.9891
Iteration: 2335; Percent complete: 58.4%; Average loss: 2.8758
Iteration: 2336; Percent complete: 58.4%; Average loss: 3.0886
Iteration: 2337; Percent complete: 58.4%; Average loss: 3.2243
Iteration: 2338; Percent complete: 58.5%; Average loss: 2.9870
Iteration: 2339; Percent complete: 58.5%; Average loss: 3.0869
Iteration: 2340; Percent complete: 58.5%; Average loss: 3.1727
Iteration: 2341; Percent complete: 58.5%; Average loss: 3.1090
Iteration: 2342; Percent complete: 58.6%; Average loss: 2.9256
Iteration: 2343; Percent complete: 58.6%; Average loss: 3.1388
Iteration: 2344; Percent complete: 58.6%; Average loss: 3.1065
Iteration: 2345; Percent complete: 58.6%; Average loss: 2.8822
Iteration: 2346; Percent complete: 58.7%; Average loss: 3.0303
Iteration: 2347; Percent complete: 58.7%; Average loss: 3.0647
Iteration: 2348; Percent complete: 58.7%; Average loss: 2.9523
Iteration: 2349; Percent complete: 58.7%; Average loss: 3.1459
Iteration: 2350; Percent complete: 58.8%; Average loss: 3.1157
Iteration: 2351; Percent complete: 58.8%; Average loss: 3.1088
Iteration: 2352; Percent complete: 58.8%; Average loss: 3.0512
Iteration: 2353; Percent complete: 58.8%; Average loss: 3.0755
Iteration: 2354; Percent complete: 58.9%; Average loss: 3.1225
Iteration: 2355; Percent complete: 58.9%; Average loss: 2.9483
Iteration: 2356; Percent complete: 58.9%; Average loss: 2.9167
Iteration: 2357; Percent complete: 58.9%; Average loss: 3.0835
Iteration: 2358; Percent complete: 59.0%; Average loss: 2.8644
Iteration: 2359; Percent complete: 59.0%; Average loss: 2.9551
Iteration: 2360; Percent complete: 59.0%; Average loss: 3.3581
Iteration: 2361; Percent complete: 59.0%; Average loss: 2.9505
Iteration: 2362; Percent complete: 59.1%; Average loss: 3.2827
Iteration: 2363; Percent complete: 59.1%; Average loss: 3.1133
Iteration: 2364; Percent complete: 59.1%; Average loss: 3.1792
Iteration: 2365; Percent complete: 59.1%; Average loss: 2.9835
Iteration: 2366; Percent complete: 59.2%; Average loss: 3.2592
Iteration: 2367; Percent complete: 59.2%; Average loss: 3.2455
Iteration: 2368; Percent complete: 59.2%; Average loss: 3.1645
Iteration: 2369; Percent complete: 59.2%; Average loss: 2.9704
Iteration: 2370; Percent complete: 59.2%; Average loss: 2.9941
Iteration: 2371; Percent complete: 59.3%; Average loss: 2.9084
Iteration: 2372; Percent complete: 59.3%; Average loss: 3.0395
Iteration: 2373; Percent complete: 59.3%; Average loss: 3.0755
Iteration: 2374; Percent complete: 59.4%; Average loss: 3.0390
Iteration: 2375; Percent complete: 59.4%; Average loss: 3.3322
Iteration: 2376; Percent complete: 59.4%; Average loss: 3.2579
Iteration: 2377; Percent complete: 59.4%; Average loss: 2.9997
Iteration: 2378; Percent complete: 59.5%; Average loss: 2.9506
Iteration: 2379; Percent complete: 59.5%; Average loss: 2.9123
Iteration: 2380; Percent complete: 59.5%; Average loss: 3.0151
Iteration: 2381; Percent complete: 59.5%; Average loss: 3.2251
Iteration: 2382; Percent complete: 59.6%; Average loss: 3.1676
Iteration: 2383; Percent complete: 59.6%; Average loss: 3.0631
Iteration: 2384; Percent complete: 59.6%; Average loss: 3.1093
Iteration: 2385; Percent complete: 59.6%; Average loss: 2.9481
Iteration: 2386; Percent complete: 59.7%; Average loss: 3.2162
Iteration: 2387; Percent complete: 59.7%; Average loss: 3.1134
Iteration: 2388; Percent complete: 59.7%; Average loss: 3.1152
Iteration: 2389; Percent complete: 59.7%; Average loss: 3.1690
Iteration: 2390; Percent complete: 59.8%; Average loss: 2.8834
Iteration: 2391; Percent complete: 59.8%; Average loss: 2.9916
Iteration: 2392; Percent complete: 59.8%; Average loss: 2.9691
Iteration: 2393; Percent complete: 59.8%; Average loss: 3.2700
Iteration: 2394; Percent complete: 59.9%; Average loss: 3.4919
Iteration: 2395; Percent complete: 59.9%; Average loss: 2.9670
Iteration: 2396; Percent complete: 59.9%; Average loss: 3.3555
Iteration: 2397; Percent complete: 59.9%; Average loss: 3.1523
Iteration: 2398; Percent complete: 60.0%; Average loss: 2.7861
Iteration: 2399; Percent complete: 60.0%; Average loss: 3.0586
Iteration: 2400; Percent complete: 60.0%; Average loss: 3.0989
Iteration: 2401; Percent complete: 60.0%; Average loss: 3.1766
Iteration: 2402; Percent complete: 60.1%; Average loss: 3.1009
Iteration: 2403; Percent complete: 60.1%; Average loss: 3.0328
Iteration: 2404; Percent complete: 60.1%; Average loss: 3.1113
Iteration: 2405; Percent complete: 60.1%; Average loss: 2.9772
Iteration: 2406; Percent complete: 60.2%; Average loss: 3.1190
Iteration: 2407; Percent complete: 60.2%; Average loss: 3.0900
Iteration: 2408; Percent complete: 60.2%; Average loss: 2.9514
Iteration: 2409; Percent complete: 60.2%; Average loss: 2.8709
Iteration: 2410; Percent complete: 60.2%; Average loss: 2.9733
Iteration: 2411; Percent complete: 60.3%; Average loss: 3.1100
Iteration: 2412; Percent complete: 60.3%; Average loss: 2.9668
Iteration: 2413; Percent complete: 60.3%; Average loss: 3.0634
Iteration: 2414; Percent complete: 60.4%; Average loss: 3.2152
Iteration: 2415; Percent complete: 60.4%; Average loss: 3.1390
Iteration: 2416; Percent complete: 60.4%; Average loss: 2.9958
Iteration: 2417; Percent complete: 60.4%; Average loss: 3.0026
Iteration: 2418; Percent complete: 60.5%; Average loss: 2.8351
Iteration: 2419; Percent complete: 60.5%; Average loss: 2.9400
Iteration: 2420; Percent complete: 60.5%; Average loss: 3.1895
Iteration: 2421; Percent complete: 60.5%; Average loss: 3.2407
Iteration: 2422; Percent complete: 60.6%; Average loss: 2.8963
Iteration: 2423; Percent complete: 60.6%; Average loss: 3.0207
Iteration: 2424; Percent complete: 60.6%; Average loss: 2.8281
Iteration: 2425; Percent complete: 60.6%; Average loss: 2.9727
Iteration: 2426; Percent complete: 60.7%; Average loss: 3.0206
Iteration: 2427; Percent complete: 60.7%; Average loss: 3.2483
Iteration: 2428; Percent complete: 60.7%; Average loss: 2.9993
Iteration: 2429; Percent complete: 60.7%; Average loss: 3.1071
Iteration: 2430; Percent complete: 60.8%; Average loss: 3.0142
Iteration: 2431; Percent complete: 60.8%; Average loss: 3.1677
Iteration: 2432; Percent complete: 60.8%; Average loss: 3.0835
Iteration: 2433; Percent complete: 60.8%; Average loss: 2.9482
Iteration: 2434; Percent complete: 60.9%; Average loss: 2.9779
Iteration: 2435; Percent complete: 60.9%; Average loss: 3.1815
Iteration: 2436; Percent complete: 60.9%; Average loss: 2.8848
Iteration: 2437; Percent complete: 60.9%; Average loss: 3.3176
Iteration: 2438; Percent complete: 61.0%; Average loss: 2.9500
Iteration: 2439; Percent complete: 61.0%; Average loss: 3.2832
Iteration: 2440; Percent complete: 61.0%; Average loss: 3.0706
Iteration: 2441; Percent complete: 61.0%; Average loss: 3.0637
Iteration: 2442; Percent complete: 61.1%; Average loss: 3.0905
Iteration: 2443; Percent complete: 61.1%; Average loss: 3.2946
Iteration: 2444; Percent complete: 61.1%; Average loss: 2.7973
Iteration: 2445; Percent complete: 61.1%; Average loss: 3.0676
Iteration: 2446; Percent complete: 61.2%; Average loss: 2.8551
Iteration: 2447; Percent complete: 61.2%; Average loss: 3.0413
Iteration: 2448; Percent complete: 61.2%; Average loss: 3.1639
Iteration: 2449; Percent complete: 61.2%; Average loss: 3.0552
Iteration: 2450; Percent complete: 61.3%; Average loss: 2.8711
Iteration: 2451; Percent complete: 61.3%; Average loss: 3.2940
Iteration: 2452; Percent complete: 61.3%; Average loss: 3.3815
Iteration: 2453; Percent complete: 61.3%; Average loss: 3.1484
Iteration: 2454; Percent complete: 61.4%; Average loss: 2.9521
Iteration: 2455; Percent complete: 61.4%; Average loss: 3.0023
Iteration: 2456; Percent complete: 61.4%; Average loss: 3.1395
Iteration: 2457; Percent complete: 61.4%; Average loss: 2.9310
Iteration: 2458; Percent complete: 61.5%; Average loss: 3.0686
Iteration: 2459; Percent complete: 61.5%; Average loss: 3.1501
Iteration: 2460; Percent complete: 61.5%; Average loss: 3.1632
Iteration: 2461; Percent complete: 61.5%; Average loss: 2.8433
Iteration: 2462; Percent complete: 61.6%; Average loss: 2.8909
Iteration: 2463; Percent complete: 61.6%; Average loss: 2.9117
Iteration: 2464; Percent complete: 61.6%; Average loss: 3.0164
Iteration: 2465; Percent complete: 61.6%; Average loss: 2.8096
Iteration: 2466; Percent complete: 61.7%; Average loss: 2.9030
Iteration: 2467; Percent complete: 61.7%; Average loss: 3.0713
Iteration: 2468; Percent complete: 61.7%; Average loss: 3.1622
Iteration: 2469; Percent complete: 61.7%; Average loss: 3.0821
Iteration: 2470; Percent complete: 61.8%; Average loss: 3.0731
Iteration: 2471; Percent complete: 61.8%; Average loss: 3.1143
Iteration: 2472; Percent complete: 61.8%; Average loss: 2.9891
Iteration: 2473; Percent complete: 61.8%; Average loss: 3.0191
Iteration: 2474; Percent complete: 61.9%; Average loss: 3.2138
Iteration: 2475; Percent complete: 61.9%; Average loss: 2.8887
Iteration: 2476; Percent complete: 61.9%; Average loss: 3.1616
Iteration: 2477; Percent complete: 61.9%; Average loss: 3.0964
Iteration: 2478; Percent complete: 62.0%; Average loss: 2.7979
Iteration: 2479; Percent complete: 62.0%; Average loss: 3.3582
Iteration: 2480; Percent complete: 62.0%; Average loss: 3.0331
Iteration: 2481; Percent complete: 62.0%; Average loss: 3.1774
Iteration: 2482; Percent complete: 62.1%; Average loss: 3.1597
Iteration: 2483; Percent complete: 62.1%; Average loss: 2.8981
Iteration: 2484; Percent complete: 62.1%; Average loss: 3.0176
Iteration: 2485; Percent complete: 62.1%; Average loss: 2.9656
Iteration: 2486; Percent complete: 62.2%; Average loss: 2.9976
Iteration: 2487; Percent complete: 62.2%; Average loss: 3.1873
Iteration: 2488; Percent complete: 62.2%; Average loss: 3.0085
Iteration: 2489; Percent complete: 62.2%; Average loss: 2.9611
Iteration: 2490; Percent complete: 62.3%; Average loss: 3.1395
Iteration: 2491; Percent complete: 62.3%; Average loss: 3.3347
Iteration: 2492; Percent complete: 62.3%; Average loss: 3.1441
Iteration: 2493; Percent complete: 62.3%; Average loss: 3.1334
Iteration: 2494; Percent complete: 62.4%; Average loss: 3.1331
Iteration: 2495; Percent complete: 62.4%; Average loss: 2.9217
Iteration: 2496; Percent complete: 62.4%; Average loss: 2.8605
Iteration: 2497; Percent complete: 62.4%; Average loss: 2.8386
Iteration: 2498; Percent complete: 62.5%; Average loss: 3.0179
Iteration: 2499; Percent complete: 62.5%; Average loss: 3.0506
Iteration: 2500; Percent complete: 62.5%; Average loss: 3.0712
Iteration: 2501; Percent complete: 62.5%; Average loss: 3.3227
Iteration: 2502; Percent complete: 62.5%; Average loss: 3.0125
Iteration: 2503; Percent complete: 62.6%; Average loss: 3.0244
Iteration: 2504; Percent complete: 62.6%; Average loss: 3.1386
Iteration: 2505; Percent complete: 62.6%; Average loss: 2.8758
Iteration: 2506; Percent complete: 62.6%; Average loss: 3.1565
Iteration: 2507; Percent complete: 62.7%; Average loss: 3.1579
Iteration: 2508; Percent complete: 62.7%; Average loss: 2.9724
Iteration: 2509; Percent complete: 62.7%; Average loss: 3.1014
Iteration: 2510; Percent complete: 62.7%; Average loss: 3.0335
Iteration: 2511; Percent complete: 62.8%; Average loss: 3.0527
Iteration: 2512; Percent complete: 62.8%; Average loss: 3.0905
Iteration: 2513; Percent complete: 62.8%; Average loss: 2.8928
Iteration: 2514; Percent complete: 62.8%; Average loss: 3.2597
Iteration: 2515; Percent complete: 62.9%; Average loss: 3.1839
Iteration: 2516; Percent complete: 62.9%; Average loss: 2.8600
Iteration: 2517; Percent complete: 62.9%; Average loss: 2.9660
Iteration: 2518; Percent complete: 62.9%; Average loss: 3.2558
Iteration: 2519; Percent complete: 63.0%; Average loss: 3.0375
Iteration: 2520; Percent complete: 63.0%; Average loss: 2.7596
Iteration: 2521; Percent complete: 63.0%; Average loss: 3.1324
Iteration: 2522; Percent complete: 63.0%; Average loss: 2.9711
Iteration: 2523; Percent complete: 63.1%; Average loss: 2.9633
Iteration: 2524; Percent complete: 63.1%; Average loss: 2.9885
Iteration: 2525; Percent complete: 63.1%; Average loss: 3.1759
Iteration: 2526; Percent complete: 63.1%; Average loss: 2.9657
Iteration: 2527; Percent complete: 63.2%; Average loss: 3.0914
Iteration: 2528; Percent complete: 63.2%; Average loss: 2.9311
Iteration: 2529; Percent complete: 63.2%; Average loss: 3.1202
Iteration: 2530; Percent complete: 63.2%; Average loss: 3.0592
Iteration: 2531; Percent complete: 63.3%; Average loss: 2.8186
Iteration: 2532; Percent complete: 63.3%; Average loss: 3.0092
Iteration: 2533; Percent complete: 63.3%; Average loss: 2.8961
Iteration: 2534; Percent complete: 63.3%; Average loss: 2.9326
Iteration: 2535; Percent complete: 63.4%; Average loss: 2.9828
Iteration: 2536; Percent complete: 63.4%; Average loss: 3.0420
Iteration: 2537; Percent complete: 63.4%; Average loss: 3.0678
Iteration: 2538; Percent complete: 63.4%; Average loss: 2.5904
Iteration: 2539; Percent complete: 63.5%; Average loss: 2.9243
Iteration: 2540; Percent complete: 63.5%; Average loss: 3.2571
Iteration: 2541; Percent complete: 63.5%; Average loss: 2.8735
Iteration: 2542; Percent complete: 63.5%; Average loss: 2.9560
Iteration: 2543; Percent complete: 63.6%; Average loss: 3.1866
Iteration: 2544; Percent complete: 63.6%; Average loss: 2.8631
Iteration: 2545; Percent complete: 63.6%; Average loss: 3.3886
Iteration: 2546; Percent complete: 63.6%; Average loss: 3.1240
Iteration: 2547; Percent complete: 63.7%; Average loss: 3.0850
Iteration: 2548; Percent complete: 63.7%; Average loss: 3.0160
Iteration: 2549; Percent complete: 63.7%; Average loss: 3.1201
Iteration: 2550; Percent complete: 63.7%; Average loss: 2.9866
Iteration: 2551; Percent complete: 63.8%; Average loss: 2.8805
Iteration: 2552; Percent complete: 63.8%; Average loss: 2.7973
Iteration: 2553; Percent complete: 63.8%; Average loss: 2.7664
Iteration: 2554; Percent complete: 63.8%; Average loss: 2.8276
Iteration: 2555; Percent complete: 63.9%; Average loss: 3.1555
Iteration: 2556; Percent complete: 63.9%; Average loss: 2.9306
Iteration: 2557; Percent complete: 63.9%; Average loss: 2.9866
Iteration: 2558; Percent complete: 63.9%; Average loss: 2.8271
Iteration: 2559; Percent complete: 64.0%; Average loss: 3.1687
Iteration: 2560; Percent complete: 64.0%; Average loss: 3.2711
Iteration: 2561; Percent complete: 64.0%; Average loss: 2.7912
Iteration: 2562; Percent complete: 64.0%; Average loss: 3.0623
Iteration: 2563; Percent complete: 64.1%; Average loss: 2.8733
Iteration: 2564; Percent complete: 64.1%; Average loss: 3.1787
Iteration: 2565; Percent complete: 64.1%; Average loss: 3.0679
Iteration: 2566; Percent complete: 64.1%; Average loss: 3.0103
Iteration: 2567; Percent complete: 64.2%; Average loss: 3.0570
Iteration: 2568; Percent complete: 64.2%; Average loss: 3.0837
Iteration: 2569; Percent complete: 64.2%; Average loss: 2.9421
Iteration: 2570; Percent complete: 64.2%; Average loss: 3.0644
Iteration: 2571; Percent complete: 64.3%; Average loss: 3.0627
Iteration: 2572; Percent complete: 64.3%; Average loss: 2.9025
Iteration: 2573; Percent complete: 64.3%; Average loss: 3.0892
Iteration: 2574; Percent complete: 64.3%; Average loss: 2.8830
Iteration: 2575; Percent complete: 64.4%; Average loss: 2.9652
Iteration: 2576; Percent complete: 64.4%; Average loss: 2.9530
Iteration: 2577; Percent complete: 64.4%; Average loss: 3.0420
Iteration: 2578; Percent complete: 64.5%; Average loss: 2.7799
Iteration: 2579; Percent complete: 64.5%; Average loss: 3.2118
Iteration: 2580; Percent complete: 64.5%; Average loss: 3.2959
Iteration: 2581; Percent complete: 64.5%; Average loss: 3.1862
Iteration: 2582; Percent complete: 64.5%; Average loss: 2.9873
Iteration: 2583; Percent complete: 64.6%; Average loss: 2.7575
Iteration: 2584; Percent complete: 64.6%; Average loss: 3.0377
Iteration: 2585; Percent complete: 64.6%; Average loss: 2.8792
Iteration: 2586; Percent complete: 64.6%; Average loss: 2.9770
Iteration: 2587; Percent complete: 64.7%; Average loss: 3.2450
Iteration: 2588; Percent complete: 64.7%; Average loss: 3.1056
Iteration: 2589; Percent complete: 64.7%; Average loss: 3.0953
Iteration: 2590; Percent complete: 64.8%; Average loss: 3.2141
Iteration: 2591; Percent complete: 64.8%; Average loss: 3.3292
Iteration: 2592; Percent complete: 64.8%; Average loss: 3.2146
Iteration: 2593; Percent complete: 64.8%; Average loss: 3.0332
Iteration: 2594; Percent complete: 64.8%; Average loss: 2.9022
Iteration: 2595; Percent complete: 64.9%; Average loss: 2.9082
Iteration: 2596; Percent complete: 64.9%; Average loss: 3.0779
Iteration: 2597; Percent complete: 64.9%; Average loss: 3.1536
Iteration: 2598; Percent complete: 65.0%; Average loss: 3.3466
Iteration: 2599; Percent complete: 65.0%; Average loss: 3.3150
Iteration: 2600; Percent complete: 65.0%; Average loss: 3.1809
Iteration: 2601; Percent complete: 65.0%; Average loss: 3.0151
Iteration: 2602; Percent complete: 65.0%; Average loss: 2.8560
Iteration: 2603; Percent complete: 65.1%; Average loss: 2.9734
Iteration: 2604; Percent complete: 65.1%; Average loss: 3.0342
Iteration: 2605; Percent complete: 65.1%; Average loss: 2.7598
Iteration: 2606; Percent complete: 65.1%; Average loss: 3.0921
Iteration: 2607; Percent complete: 65.2%; Average loss: 2.8415
Iteration: 2608; Percent complete: 65.2%; Average loss: 3.1273
Iteration: 2609; Percent complete: 65.2%; Average loss: 2.9046
Iteration: 2610; Percent complete: 65.2%; Average loss: 3.3251
Iteration: 2611; Percent complete: 65.3%; Average loss: 3.1104
Iteration: 2612; Percent complete: 65.3%; Average loss: 3.0860
Iteration: 2613; Percent complete: 65.3%; Average loss: 2.7007
Iteration: 2614; Percent complete: 65.3%; Average loss: 2.9769
Iteration: 2615; Percent complete: 65.4%; Average loss: 3.1828
Iteration: 2616; Percent complete: 65.4%; Average loss: 2.8920
Iteration: 2617; Percent complete: 65.4%; Average loss: 3.4270
Iteration: 2618; Percent complete: 65.5%; Average loss: 3.1834
Iteration: 2619; Percent complete: 65.5%; Average loss: 3.0086
Iteration: 2620; Percent complete: 65.5%; Average loss: 3.0528
Iteration: 2621; Percent complete: 65.5%; Average loss: 3.2924
Iteration: 2622; Percent complete: 65.5%; Average loss: 3.2164
Iteration: 2623; Percent complete: 65.6%; Average loss: 2.8791
Iteration: 2624; Percent complete: 65.6%; Average loss: 3.0021
Iteration: 2625; Percent complete: 65.6%; Average loss: 2.9732
Iteration: 2626; Percent complete: 65.6%; Average loss: 3.1527
Iteration: 2627; Percent complete: 65.7%; Average loss: 2.9654
Iteration: 2628; Percent complete: 65.7%; Average loss: 2.9275
Iteration: 2629; Percent complete: 65.7%; Average loss: 3.0944
Iteration: 2630; Percent complete: 65.8%; Average loss: 3.2822
Iteration: 2631; Percent complete: 65.8%; Average loss: 2.8880
Iteration: 2632; Percent complete: 65.8%; Average loss: 3.2107
Iteration: 2633; Percent complete: 65.8%; Average loss: 3.1922
Iteration: 2634; Percent complete: 65.8%; Average loss: 2.9959
Iteration: 2635; Percent complete: 65.9%; Average loss: 3.0353
Iteration: 2636; Percent complete: 65.9%; Average loss: 2.8222
Iteration: 2637; Percent complete: 65.9%; Average loss: 2.8655
Iteration: 2638; Percent complete: 66.0%; Average loss: 2.9090
Iteration: 2639; Percent complete: 66.0%; Average loss: 2.9827
Iteration: 2640; Percent complete: 66.0%; Average loss: 2.9922
Iteration: 2641; Percent complete: 66.0%; Average loss: 2.9052
Iteration: 2642; Percent complete: 66.0%; Average loss: 2.7835
Iteration: 2643; Percent complete: 66.1%; Average loss: 2.8561
Iteration: 2644; Percent complete: 66.1%; Average loss: 2.8610
Iteration: 2645; Percent complete: 66.1%; Average loss: 2.8275
Iteration: 2646; Percent complete: 66.1%; Average loss: 2.8394
Iteration: 2647; Percent complete: 66.2%; Average loss: 2.9941
Iteration: 2648; Percent complete: 66.2%; Average loss: 2.9941
Iteration: 2649; Percent complete: 66.2%; Average loss: 3.0146
Iteration: 2650; Percent complete: 66.2%; Average loss: 2.9294
Iteration: 2651; Percent complete: 66.3%; Average loss: 3.0525
Iteration: 2652; Percent complete: 66.3%; Average loss: 2.7195
Iteration: 2653; Percent complete: 66.3%; Average loss: 2.9071
Iteration: 2654; Percent complete: 66.3%; Average loss: 2.9438
Iteration: 2655; Percent complete: 66.4%; Average loss: 3.1901
Iteration: 2656; Percent complete: 66.4%; Average loss: 2.9544
Iteration: 2657; Percent complete: 66.4%; Average loss: 2.8744
Iteration: 2658; Percent complete: 66.5%; Average loss: 3.2942
Iteration: 2659; Percent complete: 66.5%; Average loss: 3.0857
Iteration: 2660; Percent complete: 66.5%; Average loss: 2.9582
Iteration: 2661; Percent complete: 66.5%; Average loss: 2.7727
Iteration: 2662; Percent complete: 66.5%; Average loss: 3.0329
Iteration: 2663; Percent complete: 66.6%; Average loss: 3.0812
Iteration: 2664; Percent complete: 66.6%; Average loss: 2.9460
Iteration: 2665; Percent complete: 66.6%; Average loss: 2.8670
Iteration: 2666; Percent complete: 66.6%; Average loss: 3.0192
Iteration: 2667; Percent complete: 66.7%; Average loss: 2.8301
Iteration: 2668; Percent complete: 66.7%; Average loss: 2.9777
Iteration: 2669; Percent complete: 66.7%; Average loss: 3.1674
Iteration: 2670; Percent complete: 66.8%; Average loss: 3.0580
Iteration: 2671; Percent complete: 66.8%; Average loss: 3.1421
Iteration: 2672; Percent complete: 66.8%; Average loss: 3.0507
Iteration: 2673; Percent complete: 66.8%; Average loss: 2.7654
Iteration: 2674; Percent complete: 66.8%; Average loss: 2.9290
Iteration: 2675; Percent complete: 66.9%; Average loss: 3.0328
Iteration: 2676; Percent complete: 66.9%; Average loss: 3.0622
Iteration: 2677; Percent complete: 66.9%; Average loss: 3.1340
Iteration: 2678; Percent complete: 67.0%; Average loss: 3.0348
Iteration: 2679; Percent complete: 67.0%; Average loss: 2.9887
Iteration: 2680; Percent complete: 67.0%; Average loss: 2.9985
Iteration: 2681; Percent complete: 67.0%; Average loss: 2.7971
Iteration: 2682; Percent complete: 67.0%; Average loss: 2.9404
Iteration: 2683; Percent complete: 67.1%; Average loss: 2.9976
Iteration: 2684; Percent complete: 67.1%; Average loss: 3.0900
Iteration: 2685; Percent complete: 67.1%; Average loss: 2.9361
Iteration: 2686; Percent complete: 67.2%; Average loss: 2.8833
Iteration: 2687; Percent complete: 67.2%; Average loss: 2.8341
Iteration: 2688; Percent complete: 67.2%; Average loss: 2.9362
Iteration: 2689; Percent complete: 67.2%; Average loss: 2.9115
Iteration: 2690; Percent complete: 67.2%; Average loss: 3.0394
Iteration: 2691; Percent complete: 67.3%; Average loss: 3.0797
Iteration: 2692; Percent complete: 67.3%; Average loss: 2.9555
Iteration: 2693; Percent complete: 67.3%; Average loss: 2.7694
Iteration: 2694; Percent complete: 67.3%; Average loss: 2.9440
Iteration: 2695; Percent complete: 67.4%; Average loss: 2.8949
Iteration: 2696; Percent complete: 67.4%; Average loss: 2.9691
Iteration: 2697; Percent complete: 67.4%; Average loss: 2.8602
Iteration: 2698; Percent complete: 67.5%; Average loss: 2.9017
Iteration: 2699; Percent complete: 67.5%; Average loss: 3.0002
Iteration: 2700; Percent complete: 67.5%; Average loss: 3.0273
Iteration: 2701; Percent complete: 67.5%; Average loss: 3.1099
Iteration: 2702; Percent complete: 67.5%; Average loss: 2.8662
Iteration: 2703; Percent complete: 67.6%; Average loss: 2.8146
Iteration: 2704; Percent complete: 67.6%; Average loss: 3.3294
Iteration: 2705; Percent complete: 67.6%; Average loss: 2.7770
Iteration: 2706; Percent complete: 67.7%; Average loss: 2.8385
Iteration: 2707; Percent complete: 67.7%; Average loss: 2.8280
Iteration: 2708; Percent complete: 67.7%; Average loss: 2.8376
Iteration: 2709; Percent complete: 67.7%; Average loss: 3.0947
Iteration: 2710; Percent complete: 67.8%; Average loss: 2.9510
Iteration: 2711; Percent complete: 67.8%; Average loss: 2.7898
Iteration: 2712; Percent complete: 67.8%; Average loss: 3.3025
Iteration: 2713; Percent complete: 67.8%; Average loss: 2.8741
Iteration: 2714; Percent complete: 67.8%; Average loss: 2.8648
Iteration: 2715; Percent complete: 67.9%; Average loss: 2.7901
Iteration: 2716; Percent complete: 67.9%; Average loss: 2.8690
Iteration: 2717; Percent complete: 67.9%; Average loss: 2.8572
Iteration: 2718; Percent complete: 68.0%; Average loss: 2.8973
Iteration: 2719; Percent complete: 68.0%; Average loss: 3.1098
Iteration: 2720; Percent complete: 68.0%; Average loss: 3.0890
Iteration: 2721; Percent complete: 68.0%; Average loss: 2.7369
Iteration: 2722; Percent complete: 68.0%; Average loss: 2.9158
Iteration: 2723; Percent complete: 68.1%; Average loss: 2.9762
Iteration: 2724; Percent complete: 68.1%; Average loss: 2.7321
Iteration: 2725; Percent complete: 68.1%; Average loss: 2.8269
Iteration: 2726; Percent complete: 68.2%; Average loss: 3.1219
Iteration: 2727; Percent complete: 68.2%; Average loss: 2.8222
Iteration: 2728; Percent complete: 68.2%; Average loss: 3.1148
Iteration: 2729; Percent complete: 68.2%; Average loss: 2.9462
Iteration: 2730; Percent complete: 68.2%; Average loss: 2.8248
Iteration: 2731; Percent complete: 68.3%; Average loss: 3.0858
Iteration: 2732; Percent complete: 68.3%; Average loss: 3.1335
Iteration: 2733; Percent complete: 68.3%; Average loss: 2.8993
Iteration: 2734; Percent complete: 68.3%; Average loss: 2.9067
Iteration: 2735; Percent complete: 68.4%; Average loss: 2.9539
Iteration: 2736; Percent complete: 68.4%; Average loss: 2.8601
Iteration: 2737; Percent complete: 68.4%; Average loss: 2.9827
Iteration: 2738; Percent complete: 68.5%; Average loss: 2.7279
Iteration: 2739; Percent complete: 68.5%; Average loss: 3.0138
Iteration: 2740; Percent complete: 68.5%; Average loss: 3.0560
Iteration: 2741; Percent complete: 68.5%; Average loss: 3.2165
Iteration: 2742; Percent complete: 68.5%; Average loss: 3.1162
Iteration: 2743; Percent complete: 68.6%; Average loss: 2.8008
Iteration: 2744; Percent complete: 68.6%; Average loss: 2.8503
Iteration: 2745; Percent complete: 68.6%; Average loss: 2.9570
Iteration: 2746; Percent complete: 68.7%; Average loss: 2.8811
Iteration: 2747; Percent complete: 68.7%; Average loss: 3.1328
Iteration: 2748; Percent complete: 68.7%; Average loss: 2.8096
Iteration: 2749; Percent complete: 68.7%; Average loss: 2.9991
Iteration: 2750; Percent complete: 68.8%; Average loss: 3.0041
Iteration: 2751; Percent complete: 68.8%; Average loss: 3.0799
Iteration: 2752; Percent complete: 68.8%; Average loss: 2.9282
Iteration: 2753; Percent complete: 68.8%; Average loss: 3.2200
Iteration: 2754; Percent complete: 68.8%; Average loss: 2.6950
Iteration: 2755; Percent complete: 68.9%; Average loss: 2.8527
Iteration: 2756; Percent complete: 68.9%; Average loss: 2.7728
Iteration: 2757; Percent complete: 68.9%; Average loss: 2.9695
Iteration: 2758; Percent complete: 69.0%; Average loss: 3.1078
Iteration: 2759; Percent complete: 69.0%; Average loss: 2.8019
Iteration: 2760; Percent complete: 69.0%; Average loss: 2.7654
Iteration: 2761; Percent complete: 69.0%; Average loss: 2.7508
Iteration: 2762; Percent complete: 69.0%; Average loss: 2.7967
Iteration: 2763; Percent complete: 69.1%; Average loss: 3.0821
Iteration: 2764; Percent complete: 69.1%; Average loss: 2.9941
Iteration: 2765; Percent complete: 69.1%; Average loss: 2.8570
Iteration: 2766; Percent complete: 69.2%; Average loss: 2.9884
Iteration: 2767; Percent complete: 69.2%; Average loss: 2.8388
Iteration: 2768; Percent complete: 69.2%; Average loss: 2.9091
Iteration: 2769; Percent complete: 69.2%; Average loss: 2.8278
Iteration: 2770; Percent complete: 69.2%; Average loss: 2.7898
Iteration: 2771; Percent complete: 69.3%; Average loss: 2.6505
Iteration: 2772; Percent complete: 69.3%; Average loss: 3.0438
Iteration: 2773; Percent complete: 69.3%; Average loss: 3.1053
Iteration: 2774; Percent complete: 69.3%; Average loss: 3.2335
Iteration: 2775; Percent complete: 69.4%; Average loss: 2.9472
Iteration: 2776; Percent complete: 69.4%; Average loss: 3.2182
Iteration: 2777; Percent complete: 69.4%; Average loss: 2.8105
Iteration: 2778; Percent complete: 69.5%; Average loss: 2.8007
Iteration: 2779; Percent complete: 69.5%; Average loss: 2.8496
Iteration: 2780; Percent complete: 69.5%; Average loss: 2.8668
Iteration: 2781; Percent complete: 69.5%; Average loss: 2.8697
Iteration: 2782; Percent complete: 69.5%; Average loss: 3.0569
Iteration: 2783; Percent complete: 69.6%; Average loss: 2.9193
Iteration: 2784; Percent complete: 69.6%; Average loss: 2.9729
Iteration: 2785; Percent complete: 69.6%; Average loss: 2.9718
Iteration: 2786; Percent complete: 69.7%; Average loss: 3.0374
Iteration: 2787; Percent complete: 69.7%; Average loss: 3.0220
Iteration: 2788; Percent complete: 69.7%; Average loss: 2.8543
Iteration: 2789; Percent complete: 69.7%; Average loss: 2.9807
Iteration: 2790; Percent complete: 69.8%; Average loss: 3.0250
Iteration: 2791; Percent complete: 69.8%; Average loss: 3.2661
Iteration: 2792; Percent complete: 69.8%; Average loss: 2.9094
Iteration: 2793; Percent complete: 69.8%; Average loss: 2.9944
Iteration: 2794; Percent complete: 69.8%; Average loss: 2.6768
Iteration: 2795; Percent complete: 69.9%; Average loss: 2.9053
Iteration: 2796; Percent complete: 69.9%; Average loss: 2.8943
Iteration: 2797; Percent complete: 69.9%; Average loss: 3.1795
Iteration: 2798; Percent complete: 70.0%; Average loss: 2.8176
Iteration: 2799; Percent complete: 70.0%; Average loss: 2.7718
Iteration: 2800; Percent complete: 70.0%; Average loss: 3.0330
Iteration: 2801; Percent complete: 70.0%; Average loss: 3.0959
Iteration: 2802; Percent complete: 70.0%; Average loss: 2.6338
Iteration: 2803; Percent complete: 70.1%; Average loss: 2.9709
Iteration: 2804; Percent complete: 70.1%; Average loss: 2.9621
Iteration: 2805; Percent complete: 70.1%; Average loss: 2.9435
Iteration: 2806; Percent complete: 70.2%; Average loss: 2.9197
Iteration: 2807; Percent complete: 70.2%; Average loss: 3.0482
Iteration: 2808; Percent complete: 70.2%; Average loss: 3.1044
Iteration: 2809; Percent complete: 70.2%; Average loss: 2.7240
Iteration: 2810; Percent complete: 70.2%; Average loss: 2.9905
Iteration: 2811; Percent complete: 70.3%; Average loss: 2.7236
Iteration: 2812; Percent complete: 70.3%; Average loss: 3.0256
Iteration: 2813; Percent complete: 70.3%; Average loss: 2.5753
Iteration: 2814; Percent complete: 70.3%; Average loss: 2.7373
Iteration: 2815; Percent complete: 70.4%; Average loss: 2.9018
Iteration: 2816; Percent complete: 70.4%; Average loss: 2.8898
Iteration: 2817; Percent complete: 70.4%; Average loss: 3.0388
Iteration: 2818; Percent complete: 70.5%; Average loss: 2.9001
Iteration: 2819; Percent complete: 70.5%; Average loss: 3.0579
Iteration: 2820; Percent complete: 70.5%; Average loss: 2.8918
Iteration: 2821; Percent complete: 70.5%; Average loss: 3.1195
Iteration: 2822; Percent complete: 70.5%; Average loss: 2.8481
Iteration: 2823; Percent complete: 70.6%; Average loss: 2.9636
Iteration: 2824; Percent complete: 70.6%; Average loss: 3.0974
Iteration: 2825; Percent complete: 70.6%; Average loss: 3.0336
Iteration: 2826; Percent complete: 70.7%; Average loss: 3.2917
Iteration: 2827; Percent complete: 70.7%; Average loss: 2.7772
Iteration: 2828; Percent complete: 70.7%; Average loss: 3.0549
Iteration: 2829; Percent complete: 70.7%; Average loss: 2.9871
Iteration: 2830; Percent complete: 70.8%; Average loss: 2.8930
Iteration: 2831; Percent complete: 70.8%; Average loss: 2.7522
Iteration: 2832; Percent complete: 70.8%; Average loss: 3.1732
Iteration: 2833; Percent complete: 70.8%; Average loss: 2.8067
Iteration: 2834; Percent complete: 70.9%; Average loss: 2.6237
Iteration: 2835; Percent complete: 70.9%; Average loss: 2.7372
Iteration: 2836; Percent complete: 70.9%; Average loss: 2.8260
Iteration: 2837; Percent complete: 70.9%; Average loss: 2.9020
Iteration: 2838; Percent complete: 71.0%; Average loss: 3.0232
Iteration: 2839; Percent complete: 71.0%; Average loss: 3.1032
Iteration: 2840; Percent complete: 71.0%; Average loss: 2.9361
Iteration: 2841; Percent complete: 71.0%; Average loss: 2.9897
Iteration: 2842; Percent complete: 71.0%; Average loss: 2.6694
Iteration: 2843; Percent complete: 71.1%; Average loss: 2.9951
Iteration: 2844; Percent complete: 71.1%; Average loss: 2.9619
Iteration: 2845; Percent complete: 71.1%; Average loss: 2.9767
Iteration: 2846; Percent complete: 71.2%; Average loss: 2.7890
Iteration: 2847; Percent complete: 71.2%; Average loss: 2.9843
Iteration: 2848; Percent complete: 71.2%; Average loss: 2.7838
Iteration: 2849; Percent complete: 71.2%; Average loss: 3.0648
Iteration: 2850; Percent complete: 71.2%; Average loss: 3.0355
Iteration: 2851; Percent complete: 71.3%; Average loss: 2.8479
Iteration: 2852; Percent complete: 71.3%; Average loss: 3.1170
Iteration: 2853; Percent complete: 71.3%; Average loss: 2.8364
Iteration: 2854; Percent complete: 71.4%; Average loss: 2.6378
Iteration: 2855; Percent complete: 71.4%; Average loss: 2.8028
Iteration: 2856; Percent complete: 71.4%; Average loss: 2.6787
Iteration: 2857; Percent complete: 71.4%; Average loss: 2.9281
Iteration: 2858; Percent complete: 71.5%; Average loss: 2.7818
Iteration: 2859; Percent complete: 71.5%; Average loss: 2.9765
Iteration: 2860; Percent complete: 71.5%; Average loss: 3.0583
Iteration: 2861; Percent complete: 71.5%; Average loss: 2.9161
Iteration: 2862; Percent complete: 71.5%; Average loss: 2.8836
Iteration: 2863; Percent complete: 71.6%; Average loss: 2.8448
Iteration: 2864; Percent complete: 71.6%; Average loss: 3.1574
Iteration: 2865; Percent complete: 71.6%; Average loss: 2.9559
Iteration: 2866; Percent complete: 71.7%; Average loss: 2.8275
Iteration: 2867; Percent complete: 71.7%; Average loss: 2.9755
Iteration: 2868; Percent complete: 71.7%; Average loss: 2.7710
Iteration: 2869; Percent complete: 71.7%; Average loss: 2.8641
Iteration: 2870; Percent complete: 71.8%; Average loss: 2.8469
Iteration: 2871; Percent complete: 71.8%; Average loss: 2.8263
Iteration: 2872; Percent complete: 71.8%; Average loss: 3.0363
Iteration: 2873; Percent complete: 71.8%; Average loss: 3.0369
Iteration: 2874; Percent complete: 71.9%; Average loss: 2.9015
Iteration: 2875; Percent complete: 71.9%; Average loss: 2.7655
Iteration: 2876; Percent complete: 71.9%; Average loss: 3.0756
Iteration: 2877; Percent complete: 71.9%; Average loss: 2.7940
Iteration: 2878; Percent complete: 72.0%; Average loss: 2.7700
Iteration: 2879; Percent complete: 72.0%; Average loss: 2.8905
Iteration: 2880; Percent complete: 72.0%; Average loss: 3.1206
Iteration: 2881; Percent complete: 72.0%; Average loss: 2.5473
Iteration: 2882; Percent complete: 72.0%; Average loss: 2.7868
Iteration: 2883; Percent complete: 72.1%; Average loss: 2.8847
Iteration: 2884; Percent complete: 72.1%; Average loss: 3.0776
Iteration: 2885; Percent complete: 72.1%; Average loss: 3.0761
Iteration: 2886; Percent complete: 72.2%; Average loss: 2.5524
Iteration: 2887; Percent complete: 72.2%; Average loss: 3.0771
Iteration: 2888; Percent complete: 72.2%; Average loss: 2.8295
Iteration: 2889; Percent complete: 72.2%; Average loss: 2.8446
Iteration: 2890; Percent complete: 72.2%; Average loss: 3.0620
Iteration: 2891; Percent complete: 72.3%; Average loss: 2.8698
Iteration: 2892; Percent complete: 72.3%; Average loss: 2.7239
Iteration: 2893; Percent complete: 72.3%; Average loss: 2.9225
Iteration: 2894; Percent complete: 72.4%; Average loss: 2.7773
Iteration: 2895; Percent complete: 72.4%; Average loss: 2.9053
Iteration: 2896; Percent complete: 72.4%; Average loss: 2.6583
Iteration: 2897; Percent complete: 72.4%; Average loss: 2.8901
Iteration: 2898; Percent complete: 72.5%; Average loss: 2.9520
Iteration: 2899; Percent complete: 72.5%; Average loss: 2.9924
Iteration: 2900; Percent complete: 72.5%; Average loss: 2.8528
Iteration: 2901; Percent complete: 72.5%; Average loss: 2.8395
Iteration: 2902; Percent complete: 72.5%; Average loss: 3.2511
Iteration: 2903; Percent complete: 72.6%; Average loss: 2.7809
Iteration: 2904; Percent complete: 72.6%; Average loss: 2.7212
Iteration: 2905; Percent complete: 72.6%; Average loss: 2.7825
Iteration: 2906; Percent complete: 72.7%; Average loss: 2.9848
Iteration: 2907; Percent complete: 72.7%; Average loss: 2.7300
Iteration: 2908; Percent complete: 72.7%; Average loss: 2.8334
Iteration: 2909; Percent complete: 72.7%; Average loss: 2.9527
Iteration: 2910; Percent complete: 72.8%; Average loss: 3.2065
Iteration: 2911; Percent complete: 72.8%; Average loss: 3.0124
Iteration: 2912; Percent complete: 72.8%; Average loss: 2.8673
Iteration: 2913; Percent complete: 72.8%; Average loss: 3.0690
Iteration: 2914; Percent complete: 72.9%; Average loss: 2.8360
Iteration: 2915; Percent complete: 72.9%; Average loss: 3.0215
Iteration: 2916; Percent complete: 72.9%; Average loss: 2.8687
Iteration: 2917; Percent complete: 72.9%; Average loss: 2.8516
Iteration: 2918; Percent complete: 73.0%; Average loss: 3.1067
Iteration: 2919; Percent complete: 73.0%; Average loss: 3.0328
Iteration: 2920; Percent complete: 73.0%; Average loss: 2.9023
Iteration: 2921; Percent complete: 73.0%; Average loss: 3.3058
Iteration: 2922; Percent complete: 73.0%; Average loss: 2.8097
Iteration: 2923; Percent complete: 73.1%; Average loss: 2.9244
Iteration: 2924; Percent complete: 73.1%; Average loss: 2.7423
Iteration: 2925; Percent complete: 73.1%; Average loss: 2.5306
Iteration: 2926; Percent complete: 73.2%; Average loss: 2.9562
Iteration: 2927; Percent complete: 73.2%; Average loss: 2.7888
Iteration: 2928; Percent complete: 73.2%; Average loss: 2.8969
Iteration: 2929; Percent complete: 73.2%; Average loss: 2.8410
Iteration: 2930; Percent complete: 73.2%; Average loss: 2.8528
Iteration: 2931; Percent complete: 73.3%; Average loss: 3.0410
Iteration: 2932; Percent complete: 73.3%; Average loss: 3.1048
Iteration: 2933; Percent complete: 73.3%; Average loss: 2.6842
Iteration: 2934; Percent complete: 73.4%; Average loss: 2.8266
Iteration: 2935; Percent complete: 73.4%; Average loss: 2.8404
Iteration: 2936; Percent complete: 73.4%; Average loss: 2.9617
Iteration: 2937; Percent complete: 73.4%; Average loss: 2.9971
Iteration: 2938; Percent complete: 73.5%; Average loss: 2.6587
Iteration: 2939; Percent complete: 73.5%; Average loss: 3.1223
Iteration: 2940; Percent complete: 73.5%; Average loss: 3.1103
Iteration: 2941; Percent complete: 73.5%; Average loss: 2.8180
Iteration: 2942; Percent complete: 73.6%; Average loss: 2.6399
Iteration: 2943; Percent complete: 73.6%; Average loss: 2.6899
Iteration: 2944; Percent complete: 73.6%; Average loss: 2.9961
Iteration: 2945; Percent complete: 73.6%; Average loss: 2.7809
Iteration: 2946; Percent complete: 73.7%; Average loss: 2.9480
Iteration: 2947; Percent complete: 73.7%; Average loss: 3.0459
Iteration: 2948; Percent complete: 73.7%; Average loss: 2.8237
Iteration: 2949; Percent complete: 73.7%; Average loss: 2.5873
Iteration: 2950; Percent complete: 73.8%; Average loss: 3.0879
Iteration: 2951; Percent complete: 73.8%; Average loss: 2.8573
Iteration: 2952; Percent complete: 73.8%; Average loss: 2.9737
Iteration: 2953; Percent complete: 73.8%; Average loss: 2.8722
Iteration: 2954; Percent complete: 73.9%; Average loss: 2.8991
Iteration: 2955; Percent complete: 73.9%; Average loss: 2.8075
Iteration: 2956; Percent complete: 73.9%; Average loss: 3.3055
Iteration: 2957; Percent complete: 73.9%; Average loss: 2.7823
Iteration: 2958; Percent complete: 74.0%; Average loss: 2.9434
Iteration: 2959; Percent complete: 74.0%; Average loss: 3.1831
Iteration: 2960; Percent complete: 74.0%; Average loss: 2.7295
Iteration: 2961; Percent complete: 74.0%; Average loss: 3.0603
Iteration: 2962; Percent complete: 74.1%; Average loss: 2.8765
Iteration: 2963; Percent complete: 74.1%; Average loss: 2.7814
Iteration: 2964; Percent complete: 74.1%; Average loss: 2.7682
Iteration: 2965; Percent complete: 74.1%; Average loss: 2.8346
Iteration: 2966; Percent complete: 74.2%; Average loss: 2.9439
Iteration: 2967; Percent complete: 74.2%; Average loss: 2.7936
Iteration: 2968; Percent complete: 74.2%; Average loss: 3.0610
Iteration: 2969; Percent complete: 74.2%; Average loss: 3.1412
Iteration: 2970; Percent complete: 74.2%; Average loss: 2.9437
Iteration: 2971; Percent complete: 74.3%; Average loss: 2.7700
Iteration: 2972; Percent complete: 74.3%; Average loss: 2.7816
Iteration: 2973; Percent complete: 74.3%; Average loss: 2.6728
Iteration: 2974; Percent complete: 74.4%; Average loss: 2.9131
Iteration: 2975; Percent complete: 74.4%; Average loss: 2.9183
Iteration: 2976; Percent complete: 74.4%; Average loss: 2.9452
Iteration: 2977; Percent complete: 74.4%; Average loss: 2.6328
Iteration: 2978; Percent complete: 74.5%; Average loss: 2.9151
Iteration: 2979; Percent complete: 74.5%; Average loss: 3.0946
Iteration: 2980; Percent complete: 74.5%; Average loss: 2.9544
Iteration: 2981; Percent complete: 74.5%; Average loss: 2.6754
Iteration: 2982; Percent complete: 74.6%; Average loss: 3.0507
Iteration: 2983; Percent complete: 74.6%; Average loss: 2.7923
Iteration: 2984; Percent complete: 74.6%; Average loss: 3.0274
Iteration: 2985; Percent complete: 74.6%; Average loss: 2.9661
Iteration: 2986; Percent complete: 74.7%; Average loss: 3.0605
Iteration: 2987; Percent complete: 74.7%; Average loss: 3.0090
Iteration: 2988; Percent complete: 74.7%; Average loss: 2.9110
Iteration: 2989; Percent complete: 74.7%; Average loss: 3.1750
Iteration: 2990; Percent complete: 74.8%; Average loss: 2.9234
Iteration: 2991; Percent complete: 74.8%; Average loss: 2.9248
Iteration: 2992; Percent complete: 74.8%; Average loss: 2.9259
Iteration: 2993; Percent complete: 74.8%; Average loss: 3.1326
Iteration: 2994; Percent complete: 74.9%; Average loss: 2.9250
Iteration: 2995; Percent complete: 74.9%; Average loss: 2.7757
Iteration: 2996; Percent complete: 74.9%; Average loss: 2.7800
Iteration: 2997; Percent complete: 74.9%; Average loss: 2.9586
Iteration: 2998; Percent complete: 75.0%; Average loss: 2.7728
Iteration: 2999; Percent complete: 75.0%; Average loss: 3.1432
Iteration: 3000; Percent complete: 75.0%; Average loss: 2.9757
Iteration: 3001; Percent complete: 75.0%; Average loss: 2.8160
Iteration: 3002; Percent complete: 75.0%; Average loss: 2.9840
Iteration: 3003; Percent complete: 75.1%; Average loss: 3.0293
Iteration: 3004; Percent complete: 75.1%; Average loss: 2.8472
Iteration: 3005; Percent complete: 75.1%; Average loss: 2.9635
Iteration: 3006; Percent complete: 75.1%; Average loss: 3.0638
Iteration: 3007; Percent complete: 75.2%; Average loss: 2.9333
Iteration: 3008; Percent complete: 75.2%; Average loss: 2.7868
Iteration: 3009; Percent complete: 75.2%; Average loss: 2.8752
Iteration: 3010; Percent complete: 75.2%; Average loss: 2.8807
Iteration: 3011; Percent complete: 75.3%; Average loss: 2.9029
Iteration: 3012; Percent complete: 75.3%; Average loss: 2.5658
Iteration: 3013; Percent complete: 75.3%; Average loss: 3.0510
Iteration: 3014; Percent complete: 75.3%; Average loss: 2.8766
Iteration: 3015; Percent complete: 75.4%; Average loss: 2.9750
Iteration: 3016; Percent complete: 75.4%; Average loss: 2.7884
Iteration: 3017; Percent complete: 75.4%; Average loss: 2.8382
Iteration: 3018; Percent complete: 75.4%; Average loss: 2.9658
Iteration: 3019; Percent complete: 75.5%; Average loss: 2.8122
Iteration: 3020; Percent complete: 75.5%; Average loss: 3.1808
Iteration: 3021; Percent complete: 75.5%; Average loss: 2.6648
Iteration: 3022; Percent complete: 75.5%; Average loss: 2.9739
Iteration: 3023; Percent complete: 75.6%; Average loss: 2.6505
Iteration: 3024; Percent complete: 75.6%; Average loss: 3.0824
Iteration: 3025; Percent complete: 75.6%; Average loss: 2.8424
Iteration: 3026; Percent complete: 75.6%; Average loss: 2.9607
Iteration: 3027; Percent complete: 75.7%; Average loss: 2.7975
Iteration: 3028; Percent complete: 75.7%; Average loss: 2.8971
Iteration: 3029; Percent complete: 75.7%; Average loss: 3.0190
Iteration: 3030; Percent complete: 75.8%; Average loss: 2.8759
Iteration: 3031; Percent complete: 75.8%; Average loss: 3.0304
Iteration: 3032; Percent complete: 75.8%; Average loss: 2.9270
Iteration: 3033; Percent complete: 75.8%; Average loss: 3.0423
Iteration: 3034; Percent complete: 75.8%; Average loss: 2.9146
Iteration: 3035; Percent complete: 75.9%; Average loss: 2.8117
Iteration: 3036; Percent complete: 75.9%; Average loss: 2.8952
Iteration: 3037; Percent complete: 75.9%; Average loss: 2.9077
Iteration: 3038; Percent complete: 75.9%; Average loss: 2.8390
Iteration: 3039; Percent complete: 76.0%; Average loss: 2.8373
Iteration: 3040; Percent complete: 76.0%; Average loss: 2.9083
Iteration: 3041; Percent complete: 76.0%; Average loss: 2.9050
Iteration: 3042; Percent complete: 76.0%; Average loss: 3.0475
Iteration: 3043; Percent complete: 76.1%; Average loss: 2.9451
Iteration: 3044; Percent complete: 76.1%; Average loss: 2.9303
Iteration: 3045; Percent complete: 76.1%; Average loss: 2.8038
Iteration: 3046; Percent complete: 76.1%; Average loss: 2.8837
Iteration: 3047; Percent complete: 76.2%; Average loss: 2.7741
Iteration: 3048; Percent complete: 76.2%; Average loss: 2.6848
Iteration: 3049; Percent complete: 76.2%; Average loss: 3.2250
Iteration: 3050; Percent complete: 76.2%; Average loss: 2.8292
Iteration: 3051; Percent complete: 76.3%; Average loss: 3.2063
Iteration: 3052; Percent complete: 76.3%; Average loss: 2.8558
Iteration: 3053; Percent complete: 76.3%; Average loss: 3.1199
Iteration: 3054; Percent complete: 76.3%; Average loss: 2.7233
Iteration: 3055; Percent complete: 76.4%; Average loss: 2.8163
Iteration: 3056; Percent complete: 76.4%; Average loss: 3.0657
Iteration: 3057; Percent complete: 76.4%; Average loss: 2.8549
Iteration: 3058; Percent complete: 76.4%; Average loss: 2.9522
Iteration: 3059; Percent complete: 76.5%; Average loss: 2.9812
Iteration: 3060; Percent complete: 76.5%; Average loss: 2.8833
Iteration: 3061; Percent complete: 76.5%; Average loss: 2.7080
Iteration: 3062; Percent complete: 76.5%; Average loss: 3.0335
Iteration: 3063; Percent complete: 76.6%; Average loss: 2.8681
Iteration: 3064; Percent complete: 76.6%; Average loss: 2.8868
Iteration: 3065; Percent complete: 76.6%; Average loss: 2.9803
Iteration: 3066; Percent complete: 76.6%; Average loss: 3.0554
Iteration: 3067; Percent complete: 76.7%; Average loss: 2.7875
Iteration: 3068; Percent complete: 76.7%; Average loss: 3.0822
Iteration: 3069; Percent complete: 76.7%; Average loss: 2.9223
Iteration: 3070; Percent complete: 76.8%; Average loss: 2.9809
Iteration: 3071; Percent complete: 76.8%; Average loss: 2.6987
Iteration: 3072; Percent complete: 76.8%; Average loss: 2.8798
Iteration: 3073; Percent complete: 76.8%; Average loss: 2.6656
Iteration: 3074; Percent complete: 76.8%; Average loss: 3.2479
Iteration: 3075; Percent complete: 76.9%; Average loss: 2.7647
Iteration: 3076; Percent complete: 76.9%; Average loss: 2.9666
Iteration: 3077; Percent complete: 76.9%; Average loss: 2.9656
Iteration: 3078; Percent complete: 77.0%; Average loss: 2.7009
Iteration: 3079; Percent complete: 77.0%; Average loss: 3.0401
Iteration: 3080; Percent complete: 77.0%; Average loss: 2.7514
Iteration: 3081; Percent complete: 77.0%; Average loss: 2.9087
Iteration: 3082; Percent complete: 77.0%; Average loss: 2.9370
Iteration: 3083; Percent complete: 77.1%; Average loss: 3.0221
Iteration: 3084; Percent complete: 77.1%; Average loss: 2.7596
Iteration: 3085; Percent complete: 77.1%; Average loss: 2.7163
Iteration: 3086; Percent complete: 77.1%; Average loss: 2.7578
Iteration: 3087; Percent complete: 77.2%; Average loss: 2.8669
Iteration: 3088; Percent complete: 77.2%; Average loss: 2.7519
Iteration: 3089; Percent complete: 77.2%; Average loss: 2.7314
Iteration: 3090; Percent complete: 77.2%; Average loss: 2.9579
Iteration: 3091; Percent complete: 77.3%; Average loss: 2.9210
Iteration: 3092; Percent complete: 77.3%; Average loss: 2.7247
Iteration: 3093; Percent complete: 77.3%; Average loss: 2.6766
Iteration: 3094; Percent complete: 77.3%; Average loss: 2.6074
Iteration: 3095; Percent complete: 77.4%; Average loss: 2.8646
Iteration: 3096; Percent complete: 77.4%; Average loss: 2.9032
Iteration: 3097; Percent complete: 77.4%; Average loss: 2.7869
Iteration: 3098; Percent complete: 77.5%; Average loss: 2.7608
Iteration: 3099; Percent complete: 77.5%; Average loss: 2.9192
Iteration: 3100; Percent complete: 77.5%; Average loss: 2.8357
Iteration: 3101; Percent complete: 77.5%; Average loss: 2.8082
Iteration: 3102; Percent complete: 77.5%; Average loss: 2.8326
Iteration: 3103; Percent complete: 77.6%; Average loss: 2.6508
Iteration: 3104; Percent complete: 77.6%; Average loss: 2.9642
Iteration: 3105; Percent complete: 77.6%; Average loss: 2.7673
Iteration: 3106; Percent complete: 77.6%; Average loss: 2.6997
Iteration: 3107; Percent complete: 77.7%; Average loss: 2.8319
Iteration: 3108; Percent complete: 77.7%; Average loss: 2.9185
Iteration: 3109; Percent complete: 77.7%; Average loss: 2.9694
Iteration: 3110; Percent complete: 77.8%; Average loss: 2.6569
Iteration: 3111; Percent complete: 77.8%; Average loss: 2.6897
Iteration: 3112; Percent complete: 77.8%; Average loss: 2.8026
Iteration: 3113; Percent complete: 77.8%; Average loss: 2.7721
Iteration: 3114; Percent complete: 77.8%; Average loss: 2.9010
Iteration: 3115; Percent complete: 77.9%; Average loss: 2.9078
Iteration: 3116; Percent complete: 77.9%; Average loss: 2.9713
Iteration: 3117; Percent complete: 77.9%; Average loss: 2.6737
Iteration: 3118; Percent complete: 78.0%; Average loss: 3.1332
Iteration: 3119; Percent complete: 78.0%; Average loss: 2.6803
Iteration: 3120; Percent complete: 78.0%; Average loss: 3.0521
Iteration: 3121; Percent complete: 78.0%; Average loss: 2.8926
Iteration: 3122; Percent complete: 78.0%; Average loss: 2.8308
Iteration: 3123; Percent complete: 78.1%; Average loss: 2.7448
Iteration: 3124; Percent complete: 78.1%; Average loss: 2.9553
Iteration: 3125; Percent complete: 78.1%; Average loss: 2.7605
Iteration: 3126; Percent complete: 78.1%; Average loss: 3.1853
Iteration: 3127; Percent complete: 78.2%; Average loss: 2.7189
Iteration: 3128; Percent complete: 78.2%; Average loss: 2.9482
Iteration: 3129; Percent complete: 78.2%; Average loss: 2.9246
Iteration: 3130; Percent complete: 78.2%; Average loss: 3.0890
Iteration: 3131; Percent complete: 78.3%; Average loss: 2.8798
Iteration: 3132; Percent complete: 78.3%; Average loss: 2.7746
Iteration: 3133; Percent complete: 78.3%; Average loss: 2.5261
Iteration: 3134; Percent complete: 78.3%; Average loss: 3.0447
Iteration: 3135; Percent complete: 78.4%; Average loss: 3.0755
Iteration: 3136; Percent complete: 78.4%; Average loss: 2.7814
Iteration: 3137; Percent complete: 78.4%; Average loss: 2.6699
Iteration: 3138; Percent complete: 78.5%; Average loss: 2.9229
Iteration: 3139; Percent complete: 78.5%; Average loss: 2.7331
Iteration: 3140; Percent complete: 78.5%; Average loss: 2.8436
Iteration: 3141; Percent complete: 78.5%; Average loss: 2.7537
Iteration: 3142; Percent complete: 78.5%; Average loss: 2.5330
Iteration: 3143; Percent complete: 78.6%; Average loss: 2.9491
Iteration: 3144; Percent complete: 78.6%; Average loss: 2.9920
Iteration: 3145; Percent complete: 78.6%; Average loss: 2.7917
Iteration: 3146; Percent complete: 78.6%; Average loss: 3.0925
Iteration: 3147; Percent complete: 78.7%; Average loss: 2.7430
Iteration: 3148; Percent complete: 78.7%; Average loss: 2.8904
Iteration: 3149; Percent complete: 78.7%; Average loss: 2.8797
Iteration: 3150; Percent complete: 78.8%; Average loss: 2.8665
Iteration: 3151; Percent complete: 78.8%; Average loss: 2.8281
Iteration: 3152; Percent complete: 78.8%; Average loss: 2.9891
Iteration: 3153; Percent complete: 78.8%; Average loss: 3.1652
Iteration: 3154; Percent complete: 78.8%; Average loss: 3.0182
Iteration: 3155; Percent complete: 78.9%; Average loss: 2.7764
Iteration: 3156; Percent complete: 78.9%; Average loss: 2.9207
Iteration: 3157; Percent complete: 78.9%; Average loss: 2.9610
Iteration: 3158; Percent complete: 79.0%; Average loss: 2.8903
Iteration: 3159; Percent complete: 79.0%; Average loss: 2.9649
Iteration: 3160; Percent complete: 79.0%; Average loss: 2.6960
Iteration: 3161; Percent complete: 79.0%; Average loss: 3.0990
Iteration: 3162; Percent complete: 79.0%; Average loss: 2.6876
Iteration: 3163; Percent complete: 79.1%; Average loss: 2.8511
Iteration: 3164; Percent complete: 79.1%; Average loss: 2.8407
Iteration: 3165; Percent complete: 79.1%; Average loss: 2.7273
Iteration: 3166; Percent complete: 79.1%; Average loss: 2.6373
Iteration: 3167; Percent complete: 79.2%; Average loss: 3.0089
Iteration: 3168; Percent complete: 79.2%; Average loss: 2.5678
Iteration: 3169; Percent complete: 79.2%; Average loss: 2.6726
Iteration: 3170; Percent complete: 79.2%; Average loss: 2.9573
Iteration: 3171; Percent complete: 79.3%; Average loss: 2.9145
Iteration: 3172; Percent complete: 79.3%; Average loss: 2.8960
Iteration: 3173; Percent complete: 79.3%; Average loss: 2.9155
Iteration: 3174; Percent complete: 79.3%; Average loss: 2.8259
Iteration: 3175; Percent complete: 79.4%; Average loss: 2.8613
Iteration: 3176; Percent complete: 79.4%; Average loss: 2.6702
Iteration: 3177; Percent complete: 79.4%; Average loss: 2.8917
Iteration: 3178; Percent complete: 79.5%; Average loss: 2.8542
Iteration: 3179; Percent complete: 79.5%; Average loss: 2.8301
Iteration: 3180; Percent complete: 79.5%; Average loss: 2.8044
Iteration: 3181; Percent complete: 79.5%; Average loss: 2.8711
Iteration: 3182; Percent complete: 79.5%; Average loss: 2.8091
Iteration: 3183; Percent complete: 79.6%; Average loss: 2.8149
Iteration: 3184; Percent complete: 79.6%; Average loss: 2.7367
Iteration: 3185; Percent complete: 79.6%; Average loss: 2.8934
Iteration: 3186; Percent complete: 79.7%; Average loss: 2.8098
Iteration: 3187; Percent complete: 79.7%; Average loss: 3.1360
Iteration: 3188; Percent complete: 79.7%; Average loss: 2.8956
Iteration: 3189; Percent complete: 79.7%; Average loss: 2.7992
Iteration: 3190; Percent complete: 79.8%; Average loss: 3.1994
Iteration: 3191; Percent complete: 79.8%; Average loss: 2.8421
Iteration: 3192; Percent complete: 79.8%; Average loss: 2.9417
Iteration: 3193; Percent complete: 79.8%; Average loss: 2.7965
Iteration: 3194; Percent complete: 79.8%; Average loss: 2.7976
Iteration: 3195; Percent complete: 79.9%; Average loss: 2.9987
Iteration: 3196; Percent complete: 79.9%; Average loss: 2.8146
Iteration: 3197; Percent complete: 79.9%; Average loss: 2.7425
Iteration: 3198; Percent complete: 80.0%; Average loss: 2.7334
Iteration: 3199; Percent complete: 80.0%; Average loss: 2.7613
Iteration: 3200; Percent complete: 80.0%; Average loss: 2.9275
Iteration: 3201; Percent complete: 80.0%; Average loss: 2.7048
Iteration: 3202; Percent complete: 80.0%; Average loss: 2.6538
Iteration: 3203; Percent complete: 80.1%; Average loss: 2.8873
Iteration: 3204; Percent complete: 80.1%; Average loss: 2.7973
Iteration: 3205; Percent complete: 80.1%; Average loss: 2.9699
Iteration: 3206; Percent complete: 80.2%; Average loss: 2.8342
Iteration: 3207; Percent complete: 80.2%; Average loss: 3.1021
Iteration: 3208; Percent complete: 80.2%; Average loss: 2.8477
Iteration: 3209; Percent complete: 80.2%; Average loss: 3.0731
Iteration: 3210; Percent complete: 80.2%; Average loss: 2.8425
Iteration: 3211; Percent complete: 80.3%; Average loss: 2.5969
Iteration: 3212; Percent complete: 80.3%; Average loss: 2.8574
Iteration: 3213; Percent complete: 80.3%; Average loss: 2.8615
Iteration: 3214; Percent complete: 80.3%; Average loss: 2.9135
Iteration: 3215; Percent complete: 80.4%; Average loss: 2.9720
Iteration: 3216; Percent complete: 80.4%; Average loss: 2.7399
Iteration: 3217; Percent complete: 80.4%; Average loss: 2.7823
Iteration: 3218; Percent complete: 80.5%; Average loss: 2.6919
Iteration: 3219; Percent complete: 80.5%; Average loss: 2.9418
Iteration: 3220; Percent complete: 80.5%; Average loss: 2.9145
Iteration: 3221; Percent complete: 80.5%; Average loss: 2.9616
Iteration: 3222; Percent complete: 80.5%; Average loss: 2.8959
Iteration: 3223; Percent complete: 80.6%; Average loss: 2.7810
Iteration: 3224; Percent complete: 80.6%; Average loss: 2.7554
Iteration: 3225; Percent complete: 80.6%; Average loss: 2.6468
Iteration: 3226; Percent complete: 80.7%; Average loss: 2.8416
Iteration: 3227; Percent complete: 80.7%; Average loss: 2.8216
Iteration: 3228; Percent complete: 80.7%; Average loss: 2.8856
Iteration: 3229; Percent complete: 80.7%; Average loss: 2.9156
Iteration: 3230; Percent complete: 80.8%; Average loss: 2.8999
Iteration: 3231; Percent complete: 80.8%; Average loss: 2.6952
Iteration: 3232; Percent complete: 80.8%; Average loss: 2.7380
Iteration: 3233; Percent complete: 80.8%; Average loss: 3.1061
Iteration: 3234; Percent complete: 80.8%; Average loss: 2.8334
Iteration: 3235; Percent complete: 80.9%; Average loss: 2.6794
Iteration: 3236; Percent complete: 80.9%; Average loss: 2.7236
Iteration: 3237; Percent complete: 80.9%; Average loss: 2.9342
Iteration: 3238; Percent complete: 81.0%; Average loss: 2.8144
Iteration: 3239; Percent complete: 81.0%; Average loss: 2.9872
Iteration: 3240; Percent complete: 81.0%; Average loss: 2.6477
Iteration: 3241; Percent complete: 81.0%; Average loss: 2.7481
Iteration: 3242; Percent complete: 81.0%; Average loss: 2.9484
Iteration: 3243; Percent complete: 81.1%; Average loss: 2.8587
Iteration: 3244; Percent complete: 81.1%; Average loss: 2.9954
Iteration: 3245; Percent complete: 81.1%; Average loss: 2.6721
Iteration: 3246; Percent complete: 81.2%; Average loss: 2.8186
Iteration: 3247; Percent complete: 81.2%; Average loss: 2.7188
Iteration: 3248; Percent complete: 81.2%; Average loss: 2.8610
Iteration: 3249; Percent complete: 81.2%; Average loss: 3.0161
Iteration: 3250; Percent complete: 81.2%; Average loss: 2.9906
Iteration: 3251; Percent complete: 81.3%; Average loss: 3.0123
Iteration: 3252; Percent complete: 81.3%; Average loss: 3.0738
Iteration: 3253; Percent complete: 81.3%; Average loss: 2.7346
Iteration: 3254; Percent complete: 81.3%; Average loss: 2.7864
Iteration: 3255; Percent complete: 81.4%; Average loss: 2.8482
Iteration: 3256; Percent complete: 81.4%; Average loss: 2.7084
Iteration: 3257; Percent complete: 81.4%; Average loss: 2.8047
Iteration: 3258; Percent complete: 81.5%; Average loss: 2.7725
Iteration: 3259; Percent complete: 81.5%; Average loss: 2.8358
Iteration: 3260; Percent complete: 81.5%; Average loss: 2.6806
Iteration: 3261; Percent complete: 81.5%; Average loss: 2.9828
Iteration: 3262; Percent complete: 81.5%; Average loss: 2.6481
Iteration: 3263; Percent complete: 81.6%; Average loss: 2.5872
Iteration: 3264; Percent complete: 81.6%; Average loss: 2.7414
Iteration: 3265; Percent complete: 81.6%; Average loss: 2.8209
Iteration: 3266; Percent complete: 81.7%; Average loss: 2.9903
Iteration: 3267; Percent complete: 81.7%; Average loss: 2.8897
Iteration: 3268; Percent complete: 81.7%; Average loss: 2.8476
Iteration: 3269; Percent complete: 81.7%; Average loss: 2.7948
Iteration: 3270; Percent complete: 81.8%; Average loss: 2.9073
Iteration: 3271; Percent complete: 81.8%; Average loss: 2.6018
Iteration: 3272; Percent complete: 81.8%; Average loss: 2.7811
Iteration: 3273; Percent complete: 81.8%; Average loss: 2.6770
Iteration: 3274; Percent complete: 81.8%; Average loss: 2.7341
Iteration: 3275; Percent complete: 81.9%; Average loss: 2.6787
Iteration: 3276; Percent complete: 81.9%; Average loss: 2.6881
Iteration: 3277; Percent complete: 81.9%; Average loss: 3.1319
Iteration: 3278; Percent complete: 82.0%; Average loss: 2.8518
Iteration: 3279; Percent complete: 82.0%; Average loss: 2.8193
Iteration: 3280; Percent complete: 82.0%; Average loss: 2.8661
Iteration: 3281; Percent complete: 82.0%; Average loss: 2.7582
Iteration: 3282; Percent complete: 82.0%; Average loss: 2.7209
Iteration: 3283; Percent complete: 82.1%; Average loss: 2.7143
Iteration: 3284; Percent complete: 82.1%; Average loss: 2.9657
Iteration: 3285; Percent complete: 82.1%; Average loss: 2.9091
Iteration: 3286; Percent complete: 82.2%; Average loss: 3.0569
Iteration: 3287; Percent complete: 82.2%; Average loss: 2.6537
Iteration: 3288; Percent complete: 82.2%; Average loss: 2.7893
Iteration: 3289; Percent complete: 82.2%; Average loss: 2.9792
Iteration: 3290; Percent complete: 82.2%; Average loss: 3.0385
Iteration: 3291; Percent complete: 82.3%; Average loss: 2.6712
Iteration: 3292; Percent complete: 82.3%; Average loss: 2.5676
Iteration: 3293; Percent complete: 82.3%; Average loss: 2.6351
Iteration: 3294; Percent complete: 82.3%; Average loss: 2.8677
Iteration: 3295; Percent complete: 82.4%; Average loss: 2.7211
Iteration: 3296; Percent complete: 82.4%; Average loss: 2.7003
Iteration: 3297; Percent complete: 82.4%; Average loss: 2.8048
Iteration: 3298; Percent complete: 82.5%; Average loss: 2.9254
Iteration: 3299; Percent complete: 82.5%; Average loss: 2.8481
Iteration: 3300; Percent complete: 82.5%; Average loss: 2.9398
Iteration: 3301; Percent complete: 82.5%; Average loss: 3.0234
Iteration: 3302; Percent complete: 82.5%; Average loss: 2.4806
Iteration: 3303; Percent complete: 82.6%; Average loss: 2.7601
Iteration: 3304; Percent complete: 82.6%; Average loss: 2.6796
Iteration: 3305; Percent complete: 82.6%; Average loss: 2.6531
Iteration: 3306; Percent complete: 82.7%; Average loss: 3.0176
Iteration: 3307; Percent complete: 82.7%; Average loss: 3.0383
Iteration: 3308; Percent complete: 82.7%; Average loss: 2.7205
Iteration: 3309; Percent complete: 82.7%; Average loss: 2.8616
Iteration: 3310; Percent complete: 82.8%; Average loss: 2.7139
Iteration: 3311; Percent complete: 82.8%; Average loss: 3.0413
Iteration: 3312; Percent complete: 82.8%; Average loss: 2.8630
Iteration: 3313; Percent complete: 82.8%; Average loss: 2.8747
Iteration: 3314; Percent complete: 82.8%; Average loss: 2.6586
Iteration: 3315; Percent complete: 82.9%; Average loss: 3.0622
Iteration: 3316; Percent complete: 82.9%; Average loss: 2.7093
Iteration: 3317; Percent complete: 82.9%; Average loss: 2.5442
Iteration: 3318; Percent complete: 83.0%; Average loss: 2.8834
Iteration: 3319; Percent complete: 83.0%; Average loss: 2.6970
Iteration: 3320; Percent complete: 83.0%; Average loss: 2.9935
Iteration: 3321; Percent complete: 83.0%; Average loss: 2.7459
Iteration: 3322; Percent complete: 83.0%; Average loss: 2.6946
Iteration: 3323; Percent complete: 83.1%; Average loss: 2.7244
Iteration: 3324; Percent complete: 83.1%; Average loss: 2.7142
Iteration: 3325; Percent complete: 83.1%; Average loss: 2.8604
Iteration: 3326; Percent complete: 83.2%; Average loss: 2.8854
Iteration: 3327; Percent complete: 83.2%; Average loss: 2.8375
Iteration: 3328; Percent complete: 83.2%; Average loss: 2.6990
Iteration: 3329; Percent complete: 83.2%; Average loss: 2.6760
Iteration: 3330; Percent complete: 83.2%; Average loss: 2.9082
Iteration: 3331; Percent complete: 83.3%; Average loss: 2.7323
Iteration: 3332; Percent complete: 83.3%; Average loss: 3.0420
Iteration: 3333; Percent complete: 83.3%; Average loss: 2.9791
Iteration: 3334; Percent complete: 83.4%; Average loss: 2.9144
Iteration: 3335; Percent complete: 83.4%; Average loss: 2.8412
Iteration: 3336; Percent complete: 83.4%; Average loss: 2.8100
Iteration: 3337; Percent complete: 83.4%; Average loss: 2.6111
Iteration: 3338; Percent complete: 83.5%; Average loss: 2.8025
Iteration: 3339; Percent complete: 83.5%; Average loss: 2.8736
Iteration: 3340; Percent complete: 83.5%; Average loss: 2.8743
Iteration: 3341; Percent complete: 83.5%; Average loss: 2.6251
Iteration: 3342; Percent complete: 83.5%; Average loss: 2.5069
Iteration: 3343; Percent complete: 83.6%; Average loss: 2.8271
Iteration: 3344; Percent complete: 83.6%; Average loss: 2.9378
Iteration: 3345; Percent complete: 83.6%; Average loss: 2.8055
Iteration: 3346; Percent complete: 83.7%; Average loss: 3.0085
Iteration: 3347; Percent complete: 83.7%; Average loss: 2.7946
Iteration: 3348; Percent complete: 83.7%; Average loss: 3.2771
Iteration: 3349; Percent complete: 83.7%; Average loss: 2.8161
Iteration: 3350; Percent complete: 83.8%; Average loss: 2.7559
Iteration: 3351; Percent complete: 83.8%; Average loss: 2.9486
Iteration: 3352; Percent complete: 83.8%; Average loss: 2.8014
Iteration: 3353; Percent complete: 83.8%; Average loss: 2.6327
Iteration: 3354; Percent complete: 83.9%; Average loss: 2.8366
Iteration: 3355; Percent complete: 83.9%; Average loss: 2.6427
Iteration: 3356; Percent complete: 83.9%; Average loss: 2.8928
Iteration: 3357; Percent complete: 83.9%; Average loss: 3.0105
Iteration: 3358; Percent complete: 84.0%; Average loss: 2.9164
Iteration: 3359; Percent complete: 84.0%; Average loss: 2.7612
Iteration: 3360; Percent complete: 84.0%; Average loss: 2.7393
Iteration: 3361; Percent complete: 84.0%; Average loss: 2.7202
Iteration: 3362; Percent complete: 84.0%; Average loss: 2.9043
Iteration: 3363; Percent complete: 84.1%; Average loss: 2.8920
Iteration: 3364; Percent complete: 84.1%; Average loss: 2.8863
Iteration: 3365; Percent complete: 84.1%; Average loss: 2.8732
Iteration: 3366; Percent complete: 84.2%; Average loss: 2.5687
Iteration: 3367; Percent complete: 84.2%; Average loss: 3.0254
Iteration: 3368; Percent complete: 84.2%; Average loss: 2.8546
Iteration: 3369; Percent complete: 84.2%; Average loss: 2.7096
Iteration: 3370; Percent complete: 84.2%; Average loss: 2.7710
Iteration: 3371; Percent complete: 84.3%; Average loss: 2.8289
Iteration: 3372; Percent complete: 84.3%; Average loss: 2.7420
Iteration: 3373; Percent complete: 84.3%; Average loss: 2.7816
Iteration: 3374; Percent complete: 84.4%; Average loss: 2.8723
Iteration: 3375; Percent complete: 84.4%; Average loss: 2.7759
Iteration: 3376; Percent complete: 84.4%; Average loss: 2.8284
Iteration: 3377; Percent complete: 84.4%; Average loss: 2.7362
Iteration: 3378; Percent complete: 84.5%; Average loss: 2.9124
Iteration: 3379; Percent complete: 84.5%; Average loss: 2.7229
Iteration: 3380; Percent complete: 84.5%; Average loss: 2.8012
Iteration: 3381; Percent complete: 84.5%; Average loss: 2.7996
Iteration: 3382; Percent complete: 84.5%; Average loss: 3.0266
Iteration: 3383; Percent complete: 84.6%; Average loss: 2.6941
Iteration: 3384; Percent complete: 84.6%; Average loss: 2.6788
Iteration: 3385; Percent complete: 84.6%; Average loss: 2.6611
Iteration: 3386; Percent complete: 84.7%; Average loss: 2.7349
Iteration: 3387; Percent complete: 84.7%; Average loss: 2.6432
Iteration: 3388; Percent complete: 84.7%; Average loss: 2.5405
Iteration: 3389; Percent complete: 84.7%; Average loss: 3.0674
Iteration: 3390; Percent complete: 84.8%; Average loss: 2.8603
Iteration: 3391; Percent complete: 84.8%; Average loss: 2.6420
Iteration: 3392; Percent complete: 84.8%; Average loss: 2.9033
Iteration: 3393; Percent complete: 84.8%; Average loss: 2.6853
Iteration: 3394; Percent complete: 84.9%; Average loss: 2.9616
Iteration: 3395; Percent complete: 84.9%; Average loss: 2.7087
Iteration: 3396; Percent complete: 84.9%; Average loss: 2.8797
Iteration: 3397; Percent complete: 84.9%; Average loss: 2.9413
Iteration: 3398; Percent complete: 85.0%; Average loss: 2.7667
Iteration: 3399; Percent complete: 85.0%; Average loss: 2.8528
Iteration: 3400; Percent complete: 85.0%; Average loss: 2.7916
Iteration: 3401; Percent complete: 85.0%; Average loss: 2.5401
Iteration: 3402; Percent complete: 85.0%; Average loss: 2.5558
Iteration: 3403; Percent complete: 85.1%; Average loss: 2.9731
Iteration: 3404; Percent complete: 85.1%; Average loss: 2.7815
Iteration: 3405; Percent complete: 85.1%; Average loss: 2.8211
Iteration: 3406; Percent complete: 85.2%; Average loss: 2.8225
Iteration: 3407; Percent complete: 85.2%; Average loss: 2.7639
Iteration: 3408; Percent complete: 85.2%; Average loss: 2.7918
Iteration: 3409; Percent complete: 85.2%; Average loss: 2.7546
Iteration: 3410; Percent complete: 85.2%; Average loss: 2.8106
Iteration: 3411; Percent complete: 85.3%; Average loss: 2.8212
Iteration: 3412; Percent complete: 85.3%; Average loss: 2.6317
Iteration: 3413; Percent complete: 85.3%; Average loss: 2.6992
Iteration: 3414; Percent complete: 85.4%; Average loss: 2.8362
Iteration: 3415; Percent complete: 85.4%; Average loss: 2.7729
Iteration: 3416; Percent complete: 85.4%; Average loss: 2.9095
Iteration: 3417; Percent complete: 85.4%; Average loss: 2.8930
Iteration: 3418; Percent complete: 85.5%; Average loss: 2.9025
Iteration: 3419; Percent complete: 85.5%; Average loss: 2.7795
Iteration: 3420; Percent complete: 85.5%; Average loss: 2.7237
Iteration: 3421; Percent complete: 85.5%; Average loss: 2.7861
Iteration: 3422; Percent complete: 85.5%; Average loss: 2.9145
Iteration: 3423; Percent complete: 85.6%; Average loss: 2.8412
Iteration: 3424; Percent complete: 85.6%; Average loss: 2.8928
Iteration: 3425; Percent complete: 85.6%; Average loss: 2.8915
Iteration: 3426; Percent complete: 85.7%; Average loss: 2.6826
Iteration: 3427; Percent complete: 85.7%; Average loss: 2.8617
Iteration: 3428; Percent complete: 85.7%; Average loss: 2.9785
Iteration: 3429; Percent complete: 85.7%; Average loss: 2.6660
Iteration: 3430; Percent complete: 85.8%; Average loss: 2.8332
Iteration: 3431; Percent complete: 85.8%; Average loss: 2.5946
Iteration: 3432; Percent complete: 85.8%; Average loss: 2.9121
Iteration: 3433; Percent complete: 85.8%; Average loss: 2.7327
Iteration: 3434; Percent complete: 85.9%; Average loss: 2.8868
Iteration: 3435; Percent complete: 85.9%; Average loss: 2.9398
Iteration: 3436; Percent complete: 85.9%; Average loss: 2.4923
Iteration: 3437; Percent complete: 85.9%; Average loss: 2.8802
Iteration: 3438; Percent complete: 86.0%; Average loss: 2.7830
Iteration: 3439; Percent complete: 86.0%; Average loss: 2.7567
Iteration: 3440; Percent complete: 86.0%; Average loss: 2.6704
Iteration: 3441; Percent complete: 86.0%; Average loss: 2.8501
Iteration: 3442; Percent complete: 86.1%; Average loss: 2.4217
Iteration: 3443; Percent complete: 86.1%; Average loss: 2.7143
Iteration: 3444; Percent complete: 86.1%; Average loss: 2.9411
Iteration: 3445; Percent complete: 86.1%; Average loss: 2.7982
Iteration: 3446; Percent complete: 86.2%; Average loss: 2.7976
Iteration: 3447; Percent complete: 86.2%; Average loss: 2.5997
Iteration: 3448; Percent complete: 86.2%; Average loss: 2.4913
Iteration: 3449; Percent complete: 86.2%; Average loss: 2.8465
Iteration: 3450; Percent complete: 86.2%; Average loss: 2.6582
Iteration: 3451; Percent complete: 86.3%; Average loss: 2.7483
Iteration: 3452; Percent complete: 86.3%; Average loss: 2.9496
Iteration: 3453; Percent complete: 86.3%; Average loss: 2.7646
Iteration: 3454; Percent complete: 86.4%; Average loss: 2.7278
Iteration: 3455; Percent complete: 86.4%; Average loss: 3.0876
Iteration: 3456; Percent complete: 86.4%; Average loss: 2.8302
Iteration: 3457; Percent complete: 86.4%; Average loss: 2.7154
Iteration: 3458; Percent complete: 86.5%; Average loss: 2.6652
Iteration: 3459; Percent complete: 86.5%; Average loss: 2.6910
Iteration: 3460; Percent complete: 86.5%; Average loss: 2.8311
Iteration: 3461; Percent complete: 86.5%; Average loss: 3.0273
Iteration: 3462; Percent complete: 86.6%; Average loss: 2.6836
Iteration: 3463; Percent complete: 86.6%; Average loss: 2.7166
Iteration: 3464; Percent complete: 86.6%; Average loss: 2.6921
Iteration: 3465; Percent complete: 86.6%; Average loss: 2.6505
Iteration: 3466; Percent complete: 86.7%; Average loss: 2.7744
Iteration: 3467; Percent complete: 86.7%; Average loss: 2.6701
Iteration: 3468; Percent complete: 86.7%; Average loss: 2.7347
Iteration: 3469; Percent complete: 86.7%; Average loss: 2.7555
Iteration: 3470; Percent complete: 86.8%; Average loss: 2.6956
Iteration: 3471; Percent complete: 86.8%; Average loss: 2.9179
Iteration: 3472; Percent complete: 86.8%; Average loss: 2.7419
Iteration: 3473; Percent complete: 86.8%; Average loss: 2.6626
Iteration: 3474; Percent complete: 86.9%; Average loss: 2.8344
Iteration: 3475; Percent complete: 86.9%; Average loss: 2.7436
Iteration: 3476; Percent complete: 86.9%; Average loss: 2.5647
Iteration: 3477; Percent complete: 86.9%; Average loss: 2.8371
Iteration: 3478; Percent complete: 87.0%; Average loss: 2.5702
Iteration: 3479; Percent complete: 87.0%; Average loss: 2.8981
Iteration: 3480; Percent complete: 87.0%; Average loss: 2.8171
Iteration: 3481; Percent complete: 87.0%; Average loss: 2.7377
Iteration: 3482; Percent complete: 87.1%; Average loss: 2.8132
Iteration: 3483; Percent complete: 87.1%; Average loss: 2.4401
Iteration: 3484; Percent complete: 87.1%; Average loss: 2.7189
Iteration: 3485; Percent complete: 87.1%; Average loss: 2.4189
Iteration: 3486; Percent complete: 87.2%; Average loss: 2.7187
Iteration: 3487; Percent complete: 87.2%; Average loss: 2.5077
Iteration: 3488; Percent complete: 87.2%; Average loss: 2.9163
Iteration: 3489; Percent complete: 87.2%; Average loss: 2.5887
Iteration: 3490; Percent complete: 87.2%; Average loss: 2.6631
Iteration: 3491; Percent complete: 87.3%; Average loss: 2.5943
Iteration: 3492; Percent complete: 87.3%; Average loss: 2.9463
Iteration: 3493; Percent complete: 87.3%; Average loss: 2.5873
Iteration: 3494; Percent complete: 87.4%; Average loss: 2.9145
Iteration: 3495; Percent complete: 87.4%; Average loss: 2.6569
Iteration: 3496; Percent complete: 87.4%; Average loss: 2.6494
Iteration: 3497; Percent complete: 87.4%; Average loss: 2.9101
Iteration: 3498; Percent complete: 87.5%; Average loss: 2.7957
Iteration: 3499; Percent complete: 87.5%; Average loss: 2.6367
Iteration: 3500; Percent complete: 87.5%; Average loss: 2.5747
Iteration: 3501; Percent complete: 87.5%; Average loss: 2.7116
Iteration: 3502; Percent complete: 87.5%; Average loss: 2.9235
Iteration: 3503; Percent complete: 87.6%; Average loss: 2.5892
Iteration: 3504; Percent complete: 87.6%; Average loss: 2.8269
Iteration: 3505; Percent complete: 87.6%; Average loss: 2.4382
Iteration: 3506; Percent complete: 87.6%; Average loss: 2.7232
Iteration: 3507; Percent complete: 87.7%; Average loss: 2.7160
Iteration: 3508; Percent complete: 87.7%; Average loss: 2.8166
Iteration: 3509; Percent complete: 87.7%; Average loss: 2.6468
Iteration: 3510; Percent complete: 87.8%; Average loss: 2.9135
Iteration: 3511; Percent complete: 87.8%; Average loss: 2.7637
Iteration: 3512; Percent complete: 87.8%; Average loss: 2.9292
Iteration: 3513; Percent complete: 87.8%; Average loss: 2.7410
Iteration: 3514; Percent complete: 87.8%; Average loss: 2.4056
Iteration: 3515; Percent complete: 87.9%; Average loss: 2.9793
Iteration: 3516; Percent complete: 87.9%; Average loss: 2.8439
Iteration: 3517; Percent complete: 87.9%; Average loss: 2.7725
Iteration: 3518; Percent complete: 87.9%; Average loss: 2.8989
Iteration: 3519; Percent complete: 88.0%; Average loss: 2.8849
Iteration: 3520; Percent complete: 88.0%; Average loss: 2.7970
Iteration: 3521; Percent complete: 88.0%; Average loss: 2.7243
Iteration: 3522; Percent complete: 88.0%; Average loss: 2.7693
Iteration: 3523; Percent complete: 88.1%; Average loss: 2.7852
Iteration: 3524; Percent complete: 88.1%; Average loss: 2.7209
Iteration: 3525; Percent complete: 88.1%; Average loss: 2.9323
Iteration: 3526; Percent complete: 88.1%; Average loss: 2.5231
Iteration: 3527; Percent complete: 88.2%; Average loss: 2.6291
Iteration: 3528; Percent complete: 88.2%; Average loss: 2.7413
Iteration: 3529; Percent complete: 88.2%; Average loss: 2.7582
Iteration: 3530; Percent complete: 88.2%; Average loss: 2.6654
Iteration: 3531; Percent complete: 88.3%; Average loss: 2.5827
Iteration: 3532; Percent complete: 88.3%; Average loss: 2.9624
Iteration: 3533; Percent complete: 88.3%; Average loss: 2.8619
Iteration: 3534; Percent complete: 88.3%; Average loss: 2.7461
Iteration: 3535; Percent complete: 88.4%; Average loss: 2.7156
Iteration: 3536; Percent complete: 88.4%; Average loss: 2.8469
Iteration: 3537; Percent complete: 88.4%; Average loss: 2.8681
Iteration: 3538; Percent complete: 88.4%; Average loss: 2.5500
Iteration: 3539; Percent complete: 88.5%; Average loss: 2.7300
Iteration: 3540; Percent complete: 88.5%; Average loss: 2.7177
Iteration: 3541; Percent complete: 88.5%; Average loss: 2.8287
Iteration: 3542; Percent complete: 88.5%; Average loss: 2.8334
Iteration: 3543; Percent complete: 88.6%; Average loss: 2.6784
Iteration: 3544; Percent complete: 88.6%; Average loss: 2.8315
Iteration: 3545; Percent complete: 88.6%; Average loss: 2.5133
Iteration: 3546; Percent complete: 88.6%; Average loss: 3.0296
Iteration: 3547; Percent complete: 88.7%; Average loss: 2.6350
Iteration: 3548; Percent complete: 88.7%; Average loss: 2.6844
Iteration: 3549; Percent complete: 88.7%; Average loss: 2.6649
Iteration: 3550; Percent complete: 88.8%; Average loss: 2.8604
Iteration: 3551; Percent complete: 88.8%; Average loss: 2.3842
Iteration: 3552; Percent complete: 88.8%; Average loss: 2.8636
Iteration: 3553; Percent complete: 88.8%; Average loss: 2.6913
Iteration: 3554; Percent complete: 88.8%; Average loss: 2.7636
Iteration: 3555; Percent complete: 88.9%; Average loss: 2.5855
Iteration: 3556; Percent complete: 88.9%; Average loss: 2.7751
Iteration: 3557; Percent complete: 88.9%; Average loss: 2.8198
Iteration: 3558; Percent complete: 88.9%; Average loss: 2.6732
Iteration: 3559; Percent complete: 89.0%; Average loss: 2.7283
Iteration: 3560; Percent complete: 89.0%; Average loss: 2.8973
Iteration: 3561; Percent complete: 89.0%; Average loss: 2.6307
Iteration: 3562; Percent complete: 89.0%; Average loss: 2.7981
Iteration: 3563; Percent complete: 89.1%; Average loss: 2.7414
Iteration: 3564; Percent complete: 89.1%; Average loss: 2.7531
Iteration: 3565; Percent complete: 89.1%; Average loss: 2.6885
Iteration: 3566; Percent complete: 89.1%; Average loss: 2.7132
Iteration: 3567; Percent complete: 89.2%; Average loss: 2.7919
Iteration: 3568; Percent complete: 89.2%; Average loss: 2.8370
Iteration: 3569; Percent complete: 89.2%; Average loss: 2.6553
Iteration: 3570; Percent complete: 89.2%; Average loss: 2.5867
Iteration: 3571; Percent complete: 89.3%; Average loss: 2.8354
Iteration: 3572; Percent complete: 89.3%; Average loss: 2.6638
Iteration: 3573; Percent complete: 89.3%; Average loss: 2.8527
Iteration: 3574; Percent complete: 89.3%; Average loss: 2.8163
Iteration: 3575; Percent complete: 89.4%; Average loss: 2.8803
Iteration: 3576; Percent complete: 89.4%; Average loss: 2.6317
Iteration: 3577; Percent complete: 89.4%; Average loss: 2.7134
Iteration: 3578; Percent complete: 89.5%; Average loss: 2.7723
Iteration: 3579; Percent complete: 89.5%; Average loss: 2.6768
Iteration: 3580; Percent complete: 89.5%; Average loss: 2.8661
Iteration: 3581; Percent complete: 89.5%; Average loss: 2.8863
Iteration: 3582; Percent complete: 89.5%; Average loss: 2.7267
Iteration: 3583; Percent complete: 89.6%; Average loss: 2.6635
Iteration: 3584; Percent complete: 89.6%; Average loss: 2.7277
Iteration: 3585; Percent complete: 89.6%; Average loss: 2.8158
Iteration: 3586; Percent complete: 89.6%; Average loss: 2.7576
Iteration: 3587; Percent complete: 89.7%; Average loss: 2.9064
Iteration: 3588; Percent complete: 89.7%; Average loss: 2.7738
Iteration: 3589; Percent complete: 89.7%; Average loss: 2.7773
Iteration: 3590; Percent complete: 89.8%; Average loss: 2.8003
Iteration: 3591; Percent complete: 89.8%; Average loss: 2.8486
Iteration: 3592; Percent complete: 89.8%; Average loss: 2.9401
Iteration: 3593; Percent complete: 89.8%; Average loss: 3.0260
Iteration: 3594; Percent complete: 89.8%; Average loss: 2.6810
Iteration: 3595; Percent complete: 89.9%; Average loss: 2.5961
Iteration: 3596; Percent complete: 89.9%; Average loss: 2.6183
Iteration: 3597; Percent complete: 89.9%; Average loss: 2.6614
Iteration: 3598; Percent complete: 90.0%; Average loss: 2.7050
Iteration: 3599; Percent complete: 90.0%; Average loss: 2.7427
Iteration: 3600; Percent complete: 90.0%; Average loss: 2.7900
Iteration: 3601; Percent complete: 90.0%; Average loss: 2.6947
Iteration: 3602; Percent complete: 90.0%; Average loss: 2.7101
Iteration: 3603; Percent complete: 90.1%; Average loss: 2.6052
Iteration: 3604; Percent complete: 90.1%; Average loss: 2.9523
Iteration: 3605; Percent complete: 90.1%; Average loss: 2.5627
Iteration: 3606; Percent complete: 90.1%; Average loss: 2.7897
Iteration: 3607; Percent complete: 90.2%; Average loss: 2.5880
Iteration: 3608; Percent complete: 90.2%; Average loss: 2.7922
Iteration: 3609; Percent complete: 90.2%; Average loss: 2.6529
Iteration: 3610; Percent complete: 90.2%; Average loss: 2.7743
Iteration: 3611; Percent complete: 90.3%; Average loss: 2.6816
Iteration: 3612; Percent complete: 90.3%; Average loss: 2.3785
Iteration: 3613; Percent complete: 90.3%; Average loss: 2.9744
Iteration: 3614; Percent complete: 90.3%; Average loss: 2.8488
Iteration: 3615; Percent complete: 90.4%; Average loss: 3.0007
Iteration: 3616; Percent complete: 90.4%; Average loss: 2.6027
Iteration: 3617; Percent complete: 90.4%; Average loss: 2.9264
Iteration: 3618; Percent complete: 90.5%; Average loss: 2.5254
Iteration: 3619; Percent complete: 90.5%; Average loss: 2.7927
Iteration: 3620; Percent complete: 90.5%; Average loss: 3.0004
Iteration: 3621; Percent complete: 90.5%; Average loss: 2.7117
Iteration: 3622; Percent complete: 90.5%; Average loss: 2.8190
Iteration: 3623; Percent complete: 90.6%; Average loss: 2.6361
Iteration: 3624; Percent complete: 90.6%; Average loss: 2.8158
Iteration: 3625; Percent complete: 90.6%; Average loss: 2.9241
Iteration: 3626; Percent complete: 90.6%; Average loss: 2.7585
Iteration: 3627; Percent complete: 90.7%; Average loss: 2.9120
Iteration: 3628; Percent complete: 90.7%; Average loss: 2.7799
Iteration: 3629; Percent complete: 90.7%; Average loss: 2.6344
Iteration: 3630; Percent complete: 90.8%; Average loss: 2.7639
Iteration: 3631; Percent complete: 90.8%; Average loss: 2.7243
Iteration: 3632; Percent complete: 90.8%; Average loss: 2.6709
Iteration: 3633; Percent complete: 90.8%; Average loss: 2.7405
Iteration: 3634; Percent complete: 90.8%; Average loss: 2.5965
Iteration: 3635; Percent complete: 90.9%; Average loss: 2.8474
Iteration: 3636; Percent complete: 90.9%; Average loss: 2.4860
Iteration: 3637; Percent complete: 90.9%; Average loss: 2.9050
Iteration: 3638; Percent complete: 91.0%; Average loss: 2.7263
Iteration: 3639; Percent complete: 91.0%; Average loss: 2.6186
Iteration: 3640; Percent complete: 91.0%; Average loss: 2.6008
Iteration: 3641; Percent complete: 91.0%; Average loss: 2.7807
Iteration: 3642; Percent complete: 91.0%; Average loss: 2.7878
Iteration: 3643; Percent complete: 91.1%; Average loss: 2.7944
Iteration: 3644; Percent complete: 91.1%; Average loss: 2.8170
Iteration: 3645; Percent complete: 91.1%; Average loss: 2.7748
Iteration: 3646; Percent complete: 91.1%; Average loss: 2.4648
Iteration: 3647; Percent complete: 91.2%; Average loss: 2.6392
Iteration: 3648; Percent complete: 91.2%; Average loss: 2.7014
Iteration: 3649; Percent complete: 91.2%; Average loss: 2.7413
Iteration: 3650; Percent complete: 91.2%; Average loss: 2.7341
Iteration: 3651; Percent complete: 91.3%; Average loss: 2.7664
Iteration: 3652; Percent complete: 91.3%; Average loss: 2.7569
Iteration: 3653; Percent complete: 91.3%; Average loss: 2.6029
Iteration: 3654; Percent complete: 91.3%; Average loss: 2.6780
Iteration: 3655; Percent complete: 91.4%; Average loss: 2.6306
Iteration: 3656; Percent complete: 91.4%; Average loss: 2.7674
Iteration: 3657; Percent complete: 91.4%; Average loss: 2.6455
Iteration: 3658; Percent complete: 91.5%; Average loss: 2.5552
Iteration: 3659; Percent complete: 91.5%; Average loss: 2.6312
Iteration: 3660; Percent complete: 91.5%; Average loss: 2.8487
Iteration: 3661; Percent complete: 91.5%; Average loss: 2.6928
Iteration: 3662; Percent complete: 91.5%; Average loss: 2.6655
Iteration: 3663; Percent complete: 91.6%; Average loss: 2.6663
Iteration: 3664; Percent complete: 91.6%; Average loss: 2.5815
Iteration: 3665; Percent complete: 91.6%; Average loss: 2.6952
Iteration: 3666; Percent complete: 91.6%; Average loss: 2.6608
Iteration: 3667; Percent complete: 91.7%; Average loss: 2.5806
Iteration: 3668; Percent complete: 91.7%; Average loss: 2.7967
Iteration: 3669; Percent complete: 91.7%; Average loss: 2.4738
Iteration: 3670; Percent complete: 91.8%; Average loss: 2.7247
Iteration: 3671; Percent complete: 91.8%; Average loss: 2.8513
Iteration: 3672; Percent complete: 91.8%; Average loss: 2.7273
Iteration: 3673; Percent complete: 91.8%; Average loss: 2.8502
Iteration: 3674; Percent complete: 91.8%; Average loss: 2.8032
Iteration: 3675; Percent complete: 91.9%; Average loss: 2.5322
Iteration: 3676; Percent complete: 91.9%; Average loss: 2.6001
Iteration: 3677; Percent complete: 91.9%; Average loss: 2.5682
Iteration: 3678; Percent complete: 92.0%; Average loss: 2.6932
Iteration: 3679; Percent complete: 92.0%; Average loss: 2.6816
Iteration: 3680; Percent complete: 92.0%; Average loss: 2.5873
Iteration: 3681; Percent complete: 92.0%; Average loss: 2.8523
Iteration: 3682; Percent complete: 92.0%; Average loss: 2.7768
Iteration: 3683; Percent complete: 92.1%; Average loss: 2.8328
Iteration: 3684; Percent complete: 92.1%; Average loss: 3.0079
Iteration: 3685; Percent complete: 92.1%; Average loss: 2.7997
Iteration: 3686; Percent complete: 92.2%; Average loss: 2.4167
Iteration: 3687; Percent complete: 92.2%; Average loss: 2.8558
Iteration: 3688; Percent complete: 92.2%; Average loss: 2.4932
Iteration: 3689; Percent complete: 92.2%; Average loss: 2.5549
Iteration: 3690; Percent complete: 92.2%; Average loss: 2.8593
Iteration: 3691; Percent complete: 92.3%; Average loss: 2.7309
Iteration: 3692; Percent complete: 92.3%; Average loss: 2.7489
Iteration: 3693; Percent complete: 92.3%; Average loss: 2.7177
Iteration: 3694; Percent complete: 92.3%; Average loss: 2.8015
Iteration: 3695; Percent complete: 92.4%; Average loss: 2.6782
Iteration: 3696; Percent complete: 92.4%; Average loss: 2.6461
Iteration: 3697; Percent complete: 92.4%; Average loss: 2.7292
Iteration: 3698; Percent complete: 92.5%; Average loss: 2.7919
Iteration: 3699; Percent complete: 92.5%; Average loss: 2.6272
Iteration: 3700; Percent complete: 92.5%; Average loss: 2.6334
Iteration: 3701; Percent complete: 92.5%; Average loss: 2.6524
Iteration: 3702; Percent complete: 92.5%; Average loss: 2.6322
Iteration: 3703; Percent complete: 92.6%; Average loss: 2.5274
Iteration: 3704; Percent complete: 92.6%; Average loss: 2.6868
Iteration: 3705; Percent complete: 92.6%; Average loss: 2.9604
Iteration: 3706; Percent complete: 92.7%; Average loss: 2.6626
Iteration: 3707; Percent complete: 92.7%; Average loss: 2.8168
Iteration: 3708; Percent complete: 92.7%; Average loss: 2.9916
Iteration: 3709; Percent complete: 92.7%; Average loss: 2.9308
Iteration: 3710; Percent complete: 92.8%; Average loss: 2.9782
Iteration: 3711; Percent complete: 92.8%; Average loss: 2.3848
Iteration: 3712; Percent complete: 92.8%; Average loss: 2.8076
Iteration: 3713; Percent complete: 92.8%; Average loss: 2.5488
Iteration: 3714; Percent complete: 92.8%; Average loss: 2.7520
Iteration: 3715; Percent complete: 92.9%; Average loss: 2.5061
Iteration: 3716; Percent complete: 92.9%; Average loss: 2.6711
Iteration: 3717; Percent complete: 92.9%; Average loss: 2.7377
Iteration: 3718; Percent complete: 93.0%; Average loss: 2.9062
Iteration: 3719; Percent complete: 93.0%; Average loss: 2.7262
Iteration: 3720; Percent complete: 93.0%; Average loss: 2.6377
Iteration: 3721; Percent complete: 93.0%; Average loss: 2.9647
Iteration: 3722; Percent complete: 93.0%; Average loss: 2.6625
Iteration: 3723; Percent complete: 93.1%; Average loss: 2.6558
Iteration: 3724; Percent complete: 93.1%; Average loss: 2.5720
Iteration: 3725; Percent complete: 93.1%; Average loss: 2.5720
Iteration: 3726; Percent complete: 93.2%; Average loss: 2.5441
Iteration: 3727; Percent complete: 93.2%; Average loss: 2.7274
Iteration: 3728; Percent complete: 93.2%; Average loss: 2.8653
Iteration: 3729; Percent complete: 93.2%; Average loss: 2.7024
Iteration: 3730; Percent complete: 93.2%; Average loss: 2.7987
Iteration: 3731; Percent complete: 93.3%; Average loss: 2.6534
Iteration: 3732; Percent complete: 93.3%; Average loss: 2.6714
Iteration: 3733; Percent complete: 93.3%; Average loss: 2.7418
Iteration: 3734; Percent complete: 93.3%; Average loss: 2.7415
Iteration: 3735; Percent complete: 93.4%; Average loss: 2.6146
Iteration: 3736; Percent complete: 93.4%; Average loss: 2.8267
Iteration: 3737; Percent complete: 93.4%; Average loss: 2.7670
Iteration: 3738; Percent complete: 93.5%; Average loss: 2.6532
Iteration: 3739; Percent complete: 93.5%; Average loss: 2.5520
Iteration: 3740; Percent complete: 93.5%; Average loss: 2.6584
Iteration: 3741; Percent complete: 93.5%; Average loss: 2.8317
Iteration: 3742; Percent complete: 93.5%; Average loss: 2.9058
Iteration: 3743; Percent complete: 93.6%; Average loss: 2.6747
Iteration: 3744; Percent complete: 93.6%; Average loss: 2.7709
Iteration: 3745; Percent complete: 93.6%; Average loss: 2.5315
Iteration: 3746; Percent complete: 93.7%; Average loss: 2.5912
Iteration: 3747; Percent complete: 93.7%; Average loss: 2.5478
Iteration: 3748; Percent complete: 93.7%; Average loss: 2.8007
Iteration: 3749; Percent complete: 93.7%; Average loss: 2.7397
Iteration: 3750; Percent complete: 93.8%; Average loss: 2.7593
Iteration: 3751; Percent complete: 93.8%; Average loss: 2.4325
Iteration: 3752; Percent complete: 93.8%; Average loss: 2.4243
Iteration: 3753; Percent complete: 93.8%; Average loss: 2.6555
Iteration: 3754; Percent complete: 93.8%; Average loss: 2.6562
Iteration: 3755; Percent complete: 93.9%; Average loss: 2.7566
Iteration: 3756; Percent complete: 93.9%; Average loss: 2.4998
Iteration: 3757; Percent complete: 93.9%; Average loss: 2.6288
Iteration: 3758; Percent complete: 94.0%; Average loss: 2.5652
Iteration: 3759; Percent complete: 94.0%; Average loss: 2.6439
Iteration: 3760; Percent complete: 94.0%; Average loss: 2.8055
Iteration: 3761; Percent complete: 94.0%; Average loss: 2.8683
Iteration: 3762; Percent complete: 94.0%; Average loss: 2.6830
Iteration: 3763; Percent complete: 94.1%; Average loss: 2.5720
Iteration: 3764; Percent complete: 94.1%; Average loss: 2.7855
Iteration: 3765; Percent complete: 94.1%; Average loss: 2.5959
Iteration: 3766; Percent complete: 94.2%; Average loss: 2.6269
Iteration: 3767; Percent complete: 94.2%; Average loss: 2.7404
Iteration: 3768; Percent complete: 94.2%; Average loss: 2.5672
Iteration: 3769; Percent complete: 94.2%; Average loss: 2.5911
Iteration: 3770; Percent complete: 94.2%; Average loss: 2.6259
Iteration: 3771; Percent complete: 94.3%; Average loss: 2.7210
Iteration: 3772; Percent complete: 94.3%; Average loss: 2.7577
Iteration: 3773; Percent complete: 94.3%; Average loss: 3.0184
Iteration: 3774; Percent complete: 94.3%; Average loss: 2.6794
Iteration: 3775; Percent complete: 94.4%; Average loss: 2.7198
Iteration: 3776; Percent complete: 94.4%; Average loss: 2.5852
Iteration: 3777; Percent complete: 94.4%; Average loss: 2.8270
Iteration: 3778; Percent complete: 94.5%; Average loss: 2.5642
Iteration: 3779; Percent complete: 94.5%; Average loss: 2.9163
Iteration: 3780; Percent complete: 94.5%; Average loss: 2.8255
Iteration: 3781; Percent complete: 94.5%; Average loss: 2.8104
Iteration: 3782; Percent complete: 94.5%; Average loss: 2.7536
Iteration: 3783; Percent complete: 94.6%; Average loss: 2.6044
Iteration: 3784; Percent complete: 94.6%; Average loss: 2.7695
Iteration: 3785; Percent complete: 94.6%; Average loss: 2.8665
Iteration: 3786; Percent complete: 94.7%; Average loss: 2.7557
Iteration: 3787; Percent complete: 94.7%; Average loss: 2.7384
Iteration: 3788; Percent complete: 94.7%; Average loss: 2.5896
Iteration: 3789; Percent complete: 94.7%; Average loss: 2.7948
Iteration: 3790; Percent complete: 94.8%; Average loss: 2.5838
Iteration: 3791; Percent complete: 94.8%; Average loss: 2.8059
Iteration: 3792; Percent complete: 94.8%; Average loss: 2.5422
Iteration: 3793; Percent complete: 94.8%; Average loss: 2.7295
Iteration: 3794; Percent complete: 94.8%; Average loss: 2.6745
Iteration: 3795; Percent complete: 94.9%; Average loss: 2.6888
Iteration: 3796; Percent complete: 94.9%; Average loss: 2.8467
Iteration: 3797; Percent complete: 94.9%; Average loss: 2.7356
Iteration: 3798; Percent complete: 95.0%; Average loss: 2.7017
Iteration: 3799; Percent complete: 95.0%; Average loss: 2.4904
Iteration: 3800; Percent complete: 95.0%; Average loss: 2.5028
Iteration: 3801; Percent complete: 95.0%; Average loss: 2.5159
Iteration: 3802; Percent complete: 95.0%; Average loss: 2.6674
Iteration: 3803; Percent complete: 95.1%; Average loss: 2.6765
Iteration: 3804; Percent complete: 95.1%; Average loss: 2.7620
Iteration: 3805; Percent complete: 95.1%; Average loss: 2.8088
Iteration: 3806; Percent complete: 95.2%; Average loss: 2.8246
Iteration: 3807; Percent complete: 95.2%; Average loss: 2.5284
Iteration: 3808; Percent complete: 95.2%; Average loss: 2.7231
Iteration: 3809; Percent complete: 95.2%; Average loss: 2.3535
Iteration: 3810; Percent complete: 95.2%; Average loss: 2.6811
Iteration: 3811; Percent complete: 95.3%; Average loss: 2.6144
Iteration: 3812; Percent complete: 95.3%; Average loss: 2.5902
Iteration: 3813; Percent complete: 95.3%; Average loss: 2.9442
Iteration: 3814; Percent complete: 95.3%; Average loss: 2.7624
Iteration: 3815; Percent complete: 95.4%; Average loss: 2.8854
Iteration: 3816; Percent complete: 95.4%; Average loss: 2.7770
Iteration: 3817; Percent complete: 95.4%; Average loss: 2.6326
Iteration: 3818; Percent complete: 95.5%; Average loss: 2.7071
Iteration: 3819; Percent complete: 95.5%; Average loss: 2.7478
Iteration: 3820; Percent complete: 95.5%; Average loss: 2.6849
Iteration: 3821; Percent complete: 95.5%; Average loss: 2.6375
Iteration: 3822; Percent complete: 95.5%; Average loss: 2.6358
Iteration: 3823; Percent complete: 95.6%; Average loss: 2.7529
Iteration: 3824; Percent complete: 95.6%; Average loss: 2.7035
Iteration: 3825; Percent complete: 95.6%; Average loss: 2.5664
Iteration: 3826; Percent complete: 95.7%; Average loss: 2.6265
Iteration: 3827; Percent complete: 95.7%; Average loss: 2.7424
Iteration: 3828; Percent complete: 95.7%; Average loss: 2.8600
Iteration: 3829; Percent complete: 95.7%; Average loss: 2.5959
Iteration: 3830; Percent complete: 95.8%; Average loss: 2.4946
Iteration: 3831; Percent complete: 95.8%; Average loss: 2.5956
Iteration: 3832; Percent complete: 95.8%; Average loss: 2.7753
Iteration: 3833; Percent complete: 95.8%; Average loss: 2.6302
Iteration: 3834; Percent complete: 95.9%; Average loss: 2.6853
Iteration: 3835; Percent complete: 95.9%; Average loss: 2.7433
Iteration: 3836; Percent complete: 95.9%; Average loss: 2.4759
Iteration: 3837; Percent complete: 95.9%; Average loss: 2.6487
Iteration: 3838; Percent complete: 96.0%; Average loss: 2.6453
Iteration: 3839; Percent complete: 96.0%; Average loss: 2.6154
Iteration: 3840; Percent complete: 96.0%; Average loss: 2.7716
Iteration: 3841; Percent complete: 96.0%; Average loss: 2.6122
Iteration: 3842; Percent complete: 96.0%; Average loss: 2.8055
Iteration: 3843; Percent complete: 96.1%; Average loss: 2.6292
Iteration: 3844; Percent complete: 96.1%; Average loss: 2.4912
Iteration: 3845; Percent complete: 96.1%; Average loss: 2.6623
Iteration: 3846; Percent complete: 96.2%; Average loss: 2.9308
Iteration: 3847; Percent complete: 96.2%; Average loss: 2.7676
Iteration: 3848; Percent complete: 96.2%; Average loss: 2.4198
Iteration: 3849; Percent complete: 96.2%; Average loss: 2.5813
Iteration: 3850; Percent complete: 96.2%; Average loss: 2.7043
Iteration: 3851; Percent complete: 96.3%; Average loss: 2.5429
Iteration: 3852; Percent complete: 96.3%; Average loss: 2.6956
Iteration: 3853; Percent complete: 96.3%; Average loss: 2.7447
Iteration: 3854; Percent complete: 96.4%; Average loss: 2.4336
Iteration: 3855; Percent complete: 96.4%; Average loss: 2.3807
Iteration: 3856; Percent complete: 96.4%; Average loss: 2.5499
Iteration: 3857; Percent complete: 96.4%; Average loss: 2.6718
Iteration: 3858; Percent complete: 96.5%; Average loss: 2.5357
Iteration: 3859; Percent complete: 96.5%; Average loss: 2.6354
Iteration: 3860; Percent complete: 96.5%; Average loss: 2.5022
Iteration: 3861; Percent complete: 96.5%; Average loss: 2.6559
Iteration: 3862; Percent complete: 96.5%; Average loss: 2.4820
Iteration: 3863; Percent complete: 96.6%; Average loss: 2.5577
Iteration: 3864; Percent complete: 96.6%; Average loss: 2.6754
Iteration: 3865; Percent complete: 96.6%; Average loss: 2.6787
Iteration: 3866; Percent complete: 96.7%; Average loss: 2.7437
Iteration: 3867; Percent complete: 96.7%; Average loss: 2.4156
Iteration: 3868; Percent complete: 96.7%; Average loss: 2.4941
Iteration: 3869; Percent complete: 96.7%; Average loss: 2.8858
Iteration: 3870; Percent complete: 96.8%; Average loss: 2.4707
Iteration: 3871; Percent complete: 96.8%; Average loss: 2.7237
Iteration: 3872; Percent complete: 96.8%; Average loss: 2.5403
Iteration: 3873; Percent complete: 96.8%; Average loss: 2.5419
Iteration: 3874; Percent complete: 96.9%; Average loss: 2.4800
Iteration: 3875; Percent complete: 96.9%; Average loss: 2.6195
Iteration: 3876; Percent complete: 96.9%; Average loss: 2.9055
Iteration: 3877; Percent complete: 96.9%; Average loss: 2.8457
Iteration: 3878; Percent complete: 97.0%; Average loss: 2.6883
Iteration: 3879; Percent complete: 97.0%; Average loss: 2.6769
Iteration: 3880; Percent complete: 97.0%; Average loss: 2.6287
Iteration: 3881; Percent complete: 97.0%; Average loss: 2.5830
Iteration: 3882; Percent complete: 97.0%; Average loss: 2.7446
Iteration: 3883; Percent complete: 97.1%; Average loss: 2.8129
Iteration: 3884; Percent complete: 97.1%; Average loss: 2.7574
Iteration: 3885; Percent complete: 97.1%; Average loss: 2.7541
Iteration: 3886; Percent complete: 97.2%; Average loss: 2.5094
Iteration: 3887; Percent complete: 97.2%; Average loss: 2.6606
Iteration: 3888; Percent complete: 97.2%; Average loss: 2.6078
Iteration: 3889; Percent complete: 97.2%; Average loss: 2.7218
Iteration: 3890; Percent complete: 97.2%; Average loss: 2.6496
Iteration: 3891; Percent complete: 97.3%; Average loss: 2.5595
Iteration: 3892; Percent complete: 97.3%; Average loss: 2.5897
Iteration: 3893; Percent complete: 97.3%; Average loss: 2.6753
Iteration: 3894; Percent complete: 97.4%; Average loss: 2.8002
Iteration: 3895; Percent complete: 97.4%; Average loss: 2.6231
Iteration: 3896; Percent complete: 97.4%; Average loss: 2.9935
Iteration: 3897; Percent complete: 97.4%; Average loss: 2.8649
Iteration: 3898; Percent complete: 97.5%; Average loss: 2.5372
Iteration: 3899; Percent complete: 97.5%; Average loss: 2.4038
Iteration: 3900; Percent complete: 97.5%; Average loss: 2.5419
Iteration: 3901; Percent complete: 97.5%; Average loss: 2.4723
Iteration: 3902; Percent complete: 97.5%; Average loss: 2.6430
Iteration: 3903; Percent complete: 97.6%; Average loss: 2.6149
Iteration: 3904; Percent complete: 97.6%; Average loss: 2.7440
Iteration: 3905; Percent complete: 97.6%; Average loss: 2.8311
Iteration: 3906; Percent complete: 97.7%; Average loss: 2.9704
Iteration: 3907; Percent complete: 97.7%; Average loss: 2.7230
Iteration: 3908; Percent complete: 97.7%; Average loss: 2.6198
Iteration: 3909; Percent complete: 97.7%; Average loss: 2.6338
Iteration: 3910; Percent complete: 97.8%; Average loss: 2.5948
Iteration: 3911; Percent complete: 97.8%; Average loss: 2.8240
Iteration: 3912; Percent complete: 97.8%; Average loss: 2.6604
Iteration: 3913; Percent complete: 97.8%; Average loss: 2.6387
Iteration: 3914; Percent complete: 97.9%; Average loss: 2.8064
Iteration: 3915; Percent complete: 97.9%; Average loss: 2.5456
Iteration: 3916; Percent complete: 97.9%; Average loss: 2.9808
Iteration: 3917; Percent complete: 97.9%; Average loss: 2.5289
Iteration: 3918; Percent complete: 98.0%; Average loss: 2.7635
Iteration: 3919; Percent complete: 98.0%; Average loss: 2.4748
Iteration: 3920; Percent complete: 98.0%; Average loss: 2.6981
Iteration: 3921; Percent complete: 98.0%; Average loss: 2.5608
Iteration: 3922; Percent complete: 98.0%; Average loss: 2.4377
Iteration: 3923; Percent complete: 98.1%; Average loss: 2.5706
Iteration: 3924; Percent complete: 98.1%; Average loss: 2.6116
Iteration: 3925; Percent complete: 98.1%; Average loss: 2.6445
Iteration: 3926; Percent complete: 98.2%; Average loss: 2.4917
Iteration: 3927; Percent complete: 98.2%; Average loss: 2.5542
Iteration: 3928; Percent complete: 98.2%; Average loss: 2.7069
Iteration: 3929; Percent complete: 98.2%; Average loss: 2.4430
Iteration: 3930; Percent complete: 98.2%; Average loss: 2.7232
Iteration: 3931; Percent complete: 98.3%; Average loss: 2.7742
Iteration: 3932; Percent complete: 98.3%; Average loss: 2.8234
Iteration: 3933; Percent complete: 98.3%; Average loss: 2.5556
Iteration: 3934; Percent complete: 98.4%; Average loss: 2.7014
Iteration: 3935; Percent complete: 98.4%; Average loss: 2.3705
Iteration: 3936; Percent complete: 98.4%; Average loss: 2.8922
Iteration: 3937; Percent complete: 98.4%; Average loss: 2.7020
Iteration: 3938; Percent complete: 98.5%; Average loss: 2.7894
Iteration: 3939; Percent complete: 98.5%; Average loss: 2.8656
Iteration: 3940; Percent complete: 98.5%; Average loss: 2.4996
Iteration: 3941; Percent complete: 98.5%; Average loss: 2.6100
Iteration: 3942; Percent complete: 98.6%; Average loss: 2.6502
Iteration: 3943; Percent complete: 98.6%; Average loss: 2.8048
Iteration: 3944; Percent complete: 98.6%; Average loss: 2.3748
Iteration: 3945; Percent complete: 98.6%; Average loss: 2.7153
Iteration: 3946; Percent complete: 98.7%; Average loss: 2.4635
Iteration: 3947; Percent complete: 98.7%; Average loss: 2.4321
Iteration: 3948; Percent complete: 98.7%; Average loss: 2.6548
Iteration: 3949; Percent complete: 98.7%; Average loss: 2.9084
Iteration: 3950; Percent complete: 98.8%; Average loss: 2.5761
Iteration: 3951; Percent complete: 98.8%; Average loss: 2.5203
Iteration: 3952; Percent complete: 98.8%; Average loss: 2.4818
Iteration: 3953; Percent complete: 98.8%; Average loss: 2.4826
Iteration: 3954; Percent complete: 98.9%; Average loss: 2.7753
Iteration: 3955; Percent complete: 98.9%; Average loss: 2.5868
Iteration: 3956; Percent complete: 98.9%; Average loss: 2.5145
Iteration: 3957; Percent complete: 98.9%; Average loss: 2.7557
Iteration: 3958; Percent complete: 99.0%; Average loss: 2.4651
Iteration: 3959; Percent complete: 99.0%; Average loss: 2.8000
Iteration: 3960; Percent complete: 99.0%; Average loss: 2.5053
Iteration: 3961; Percent complete: 99.0%; Average loss: 2.5581
Iteration: 3962; Percent complete: 99.1%; Average loss: 2.7720
Iteration: 3963; Percent complete: 99.1%; Average loss: 2.5942
Iteration: 3964; Percent complete: 99.1%; Average loss: 2.6074
Iteration: 3965; Percent complete: 99.1%; Average loss: 2.3909
Iteration: 3966; Percent complete: 99.2%; Average loss: 2.3233
Iteration: 3967; Percent complete: 99.2%; Average loss: 2.6634
Iteration: 3968; Percent complete: 99.2%; Average loss: 2.7464
Iteration: 3969; Percent complete: 99.2%; Average loss: 2.6072
Iteration: 3970; Percent complete: 99.2%; Average loss: 2.6010
Iteration: 3971; Percent complete: 99.3%; Average loss: 2.9934
Iteration: 3972; Percent complete: 99.3%; Average loss: 2.6264
Iteration: 3973; Percent complete: 99.3%; Average loss: 2.4987
Iteration: 3974; Percent complete: 99.4%; Average loss: 2.9340
Iteration: 3975; Percent complete: 99.4%; Average loss: 2.5823
Iteration: 3976; Percent complete: 99.4%; Average loss: 2.5991
Iteration: 3977; Percent complete: 99.4%; Average loss: 2.4932
Iteration: 3978; Percent complete: 99.5%; Average loss: 2.7894
Iteration: 3979; Percent complete: 99.5%; Average loss: 2.7963
Iteration: 3980; Percent complete: 99.5%; Average loss: 2.8088
Iteration: 3981; Percent complete: 99.5%; Average loss: 2.5456
Iteration: 3982; Percent complete: 99.6%; Average loss: 2.7043
Iteration: 3983; Percent complete: 99.6%; Average loss: 2.5024
Iteration: 3984; Percent complete: 99.6%; Average loss: 2.8903
Iteration: 3985; Percent complete: 99.6%; Average loss: 2.9088
Iteration: 3986; Percent complete: 99.7%; Average loss: 2.6033
Iteration: 3987; Percent complete: 99.7%; Average loss: 2.6790
Iteration: 3988; Percent complete: 99.7%; Average loss: 2.7241
Iteration: 3989; Percent complete: 99.7%; Average loss: 2.7518
Iteration: 3990; Percent complete: 99.8%; Average loss: 2.8316
Iteration: 3991; Percent complete: 99.8%; Average loss: 2.5607
Iteration: 3992; Percent complete: 99.8%; Average loss: 2.5873
Iteration: 3993; Percent complete: 99.8%; Average loss: 2.5784
Iteration: 3994; Percent complete: 99.9%; Average loss: 2.5063
Iteration: 3995; Percent complete: 99.9%; Average loss: 2.8685
Iteration: 3996; Percent complete: 99.9%; Average loss: 2.4874
Iteration: 3997; Percent complete: 99.9%; Average loss: 2.5955
Iteration: 3998; Percent complete: 100.0%; Average loss: 2.7564
Iteration: 3999; Percent complete: 100.0%; Average loss: 2.4255
Iteration: 4000; Percent complete: 100.0%; Average loss: 2.4154

Run Evaluation

To chat with your model, run the following block.

# Set dropout layers to ``eval`` mode
encoder.eval()
decoder.eval()

# Initialize search module
searcher = GreedySearchDecoder(encoder, decoder)

# Begin chatting (uncomment and run the following line to begin)
# evaluateInput(encoder, decoder, searcher, voc)

Conclusion

That’s all for this one, folks. Congratulations, you now know the fundamentals to building a generative chatbot model! If you’re interested, you can try tailoring the chatbot’s behavior by tweaking the model and training parameters and customizing the data that you train the model on.

Check out the other tutorials for more cool deep learning applications in PyTorch!