beginner/chatbot_tutorial

Run in Google Colab

Colab

Download Notebook

Notebook

View on GitHub

GitHub

Chatbot Tutorial

Created On: Aug 14, 2018 | Last Updated: Jan 24, 2025 | Last Verified: Nov 05, 2024

Author: Matthew Inkawhich

In this tutorial, we explore a fun and interesting use-case of recurrent sequence-to-sequence models. We will train a simple chatbot using movie scripts from the Cornell Movie-Dialogs Corpus.

Conversational models are a hot topic in artificial intelligence research. Chatbots can be found in a variety of settings, including customer service applications and online helpdesks. These bots are often powered by retrieval-based models, which output predefined responses to questions of certain forms. In a highly restricted domain like a company’s IT helpdesk, these models may be sufficient, however, they are not robust enough for more general use-cases. Teaching a machine to carry out a meaningful conversation with a human in multiple domains is a research question that is far from solved. Recently, the deep learning boom has allowed for powerful generative models like Google’s Neural Conversational Model, which marks a large step towards multi-domain generative conversational models. In this tutorial, we will implement this kind of model in PyTorch.

> hello?
Bot: hello .
> where am I?
Bot: you re in a hospital .
> who are you?
Bot: i m a lawyer .
> how are you doing?
Bot: i m fine .
> are you my friend?
Bot: no .
> you're under arrest
Bot: i m trying to help you !
> i'm just kidding
Bot: i m sorry .
> where are you from?
Bot: san francisco .
> it's time for me to leave
Bot: i know .
> goodbye
Bot: goodbye .

Tutorial Highlights

• Handle loading and preprocessing of Cornell Movie-Dialogs Corpus dataset

• Implement a sequence-to-sequence model with Luong attention mechanism(s)

• Jointly train encoder and decoder models using mini-batches

• Implement greedy-search decoding module

• Interact with trained chatbot

Acknowledgments

This tutorial borrows code from the following sources:

1. Yuan-Kuei Wu’s pytorch-chatbot implementation: ywk991112/pytorch-chatbot

2. Sean Robertson’s practical-pytorch seq2seq-translation example: spro/practical-pytorch

3. FloydHub Cornell Movie Corpus preprocessing code: floydhub/textutil-preprocess-cornell-movie-corpus

Preparations

To get started, download the Movie-Dialogs Corpus zip file.

# and put in a ``data/`` directory under the current directory.
#
# After that, let’s import some necessities.
#

import torch
from torch.jit import script, trace
import torch.nn as nn
from torch import optim
import torch.nn.functional as F
import csv
import random
import re
import os
import unicodedata
import codecs
from io import open
import itertools
import math
import json


# If the current `accelerator <https://pytorch.org/docs/stable/torch.html#accelerators>`__ is available,
# we will use it. Otherwise, we use the CPU.
device = torch.accelerator.current_accelerator().type if torch.accelerator.is_available() else "cpu"
print(f"Using {device} device")

Using cuda device

Load & Preprocess Data

The next step is to reformat our data file and load the data into structures that we can work with.

The Cornell Movie-Dialogs Corpus is a rich dataset of movie character dialog:

• 220,579 conversational exchanges between 10,292 pairs of movie characters

• 9,035 characters from 617 movies

• 304,713 total utterances

This dataset is large and diverse, and there is a great variation of language formality, time periods, sentiment, etc. Our hope is that this diversity makes our model robust to many forms of inputs and queries.

First, we’ll take a look at some lines of our datafile to see the original format.

corpus_name = "movie-corpus"
corpus = os.path.join("data", corpus_name)

def printLines(file, n=10):
    with open(file, 'rb') as datafile:
        lines = datafile.readlines()
    for line in lines[:n]:
        print(line)

printLines(os.path.join(corpus, "utterances.jsonl"))

b'{"id": "L1045", "conversation_id": "L1044", "text": "They do not!", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "They", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "not", "tag": "RB", "dep": "neg", "up": 1, "dn": []}, {"tok": "!", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": "L1044", "timestamp": null, "vectors": []}\n'
b'{"id": "L1044", "conversation_id": "L1044", "text": "They do to!", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "They", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "to", "tag": "TO", "dep": "dobj", "up": 1, "dn": []}, {"tok": "!", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L985", "conversation_id": "L984", "text": "I hope so.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "I", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "hope", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "so", "tag": "RB", "dep": "advmod", "up": 1, "dn": []}, {"tok": ".", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": "L984", "timestamp": null, "vectors": []}\n'
b'{"id": "L984", "conversation_id": "L984", "text": "She okay?", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "She", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "okay", "tag": "RB", "dep": "ROOT", "dn": [0, 2]}, {"tok": "?", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L925", "conversation_id": "L924", "text": "Let\'s go.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Let", "tag": "VB", "dep": "ROOT", "dn": [2, 3]}, {"tok": "\'s", "tag": "PRP", "dep": "nsubj", "up": 2, "dn": []}, {"tok": "go", "tag": "VB", "dep": "ccomp", "up": 0, "dn": [1]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 0, "dn": []}]}]}, "reply-to": "L924", "timestamp": null, "vectors": []}\n'
b'{"id": "L924", "conversation_id": "L924", "text": "Wow", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Wow", "tag": "UH", "dep": "ROOT", "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L872", "conversation_id": "L870", "text": "Okay -- you\'re gonna need to learn how to lie.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 4, "toks": [{"tok": "Okay", "tag": "UH", "dep": "intj", "up": 4, "dn": []}, {"tok": "--", "tag": ":", "dep": "punct", "up": 4, "dn": []}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 4, "dn": []}, {"tok": "\'re", "tag": "VBP", "dep": "aux", "up": 4, "dn": []}, {"tok": "gon", "tag": "VBG", "dep": "ROOT", "dn": [0, 1, 2, 3, 6, 12]}, {"tok": "na", "tag": "TO", "dep": "aux", "up": 6, "dn": []}, {"tok": "need", "tag": "VB", "dep": "xcomp", "up": 4, "dn": [5, 8]}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 8, "dn": []}, {"tok": "learn", "tag": "VB", "dep": "xcomp", "up": 6, "dn": [7, 11]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 11, "dn": []}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 11, "dn": []}, {"tok": "lie", "tag": "VB", "dep": "xcomp", "up": 8, "dn": [9, 10]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 4, "dn": []}]}]}, "reply-to": "L871", "timestamp": null, "vectors": []}\n'
b'{"id": "L871", "conversation_id": "L870", "text": "No", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "No", "tag": "UH", "dep": "ROOT", "dn": []}]}]}, "reply-to": "L870", "timestamp": null, "vectors": []}\n'
b'{"id": "L870", "conversation_id": "L870", "text": "I\'m kidding.  You know how sometimes you just become this \\"persona\\"?  And you don\'t know how to quit?", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 2, "toks": [{"tok": "I", "tag": "PRP", "dep": "nsubj", "up": 2, "dn": []}, {"tok": "\'m", "tag": "VBP", "dep": "aux", "up": 2, "dn": []}, {"tok": "kidding", "tag": "VBG", "dep": "ROOT", "dn": [0, 1, 3]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 2, "dn": [4]}, {"tok": " ", "tag": "_SP", "dep": "", "up": 3, "dn": []}]}, {"rt": 1, "toks": [{"tok": "You", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "know", "tag": "VBP", "dep": "ROOT", "dn": [0, 6, 11]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 3, "dn": []}, {"tok": "sometimes", "tag": "RB", "dep": "advmod", "up": 6, "dn": [2]}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 6, "dn": []}, {"tok": "just", "tag": "RB", "dep": "advmod", "up": 6, "dn": []}, {"tok": "become", "tag": "VBP", "dep": "ccomp", "up": 1, "dn": [3, 4, 5, 9]}, {"tok": "this", "tag": "DT", "dep": "det", "up": 9, "dn": []}, {"tok": "\\"", "tag": "``", "dep": "punct", "up": 9, "dn": []}, {"tok": "persona", "tag": "NN", "dep": "attr", "up": 6, "dn": [7, 8, 10]}, {"tok": "\\"", "tag": "\'\'", "dep": "punct", "up": 9, "dn": []}, {"tok": "?", "tag": ".", "dep": "punct", "up": 1, "dn": [12]}, {"tok": " ", "tag": "_SP", "dep": "", "up": 11, "dn": []}]}, {"rt": 4, "toks": [{"tok": "And", "tag": "CC", "dep": "cc", "up": 4, "dn": []}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 4, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "aux", "up": 4, "dn": []}, {"tok": "n\'t", "tag": "RB", "dep": "neg", "up": 4, "dn": []}, {"tok": "know", "tag": "VB", "dep": "ROOT", "dn": [0, 1, 2, 3, 7, 8]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 7, "dn": []}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 7, "dn": []}, {"tok": "quit", "tag": "VB", "dep": "xcomp", "up": 4, "dn": [5, 6]}, {"tok": "?", "tag": ".", "dep": "punct", "up": 4, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L869", "conversation_id": "L866", "text": "Like my fear of wearing pastels?", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Like", "tag": "IN", "dep": "ROOT", "dn": [2, 6]}, {"tok": "my", "tag": "PRP$", "dep": "poss", "up": 2, "dn": []}, {"tok": "fear", "tag": "NN", "dep": "pobj", "up": 0, "dn": [1, 3]}, {"tok": "of", "tag": "IN", "dep": "prep", "up": 2, "dn": [4]}, {"tok": "wearing", "tag": "VBG", "dep": "pcomp", "up": 3, "dn": [5]}, {"tok": "pastels", "tag": "NNS", "dep": "dobj", "up": 4, "dn": []}, {"tok": "?", "tag": ".", "dep": "punct", "up": 0, "dn": []}]}]}, "reply-to": "L868", "timestamp": null, "vectors": []}\n'

Create formatted data file

For convenience, we’ll create a nicely formatted data file in which each line contains a tab-separated query sentence and a response sentence pair.

The following functions facilitate the parsing of the raw utterances.jsonl data file.

• loadLinesAndConversations splits each line of the file into a dictionary of lines with fields: lineID, characterID, and text and then groups them into conversations with fields: conversationID, movieID, and lines.

• extractSentencePairs extracts pairs of sentences from conversations

# Splits each line of the file to create lines and conversations
def loadLinesAndConversations(fileName):
    lines = {}
    conversations = {}
    with open(fileName, 'r', encoding='iso-8859-1') as f:
        for line in f:
            lineJson = json.loads(line)
            # Extract fields for line object
            lineObj = {}
            lineObj["lineID"] = lineJson["id"]
            lineObj["characterID"] = lineJson["speaker"]
            lineObj["text"] = lineJson["text"]
            lines[lineObj['lineID']] = lineObj

            # Extract fields for conversation object
            if lineJson["conversation_id"] not in conversations:
                convObj = {}
                convObj["conversationID"] = lineJson["conversation_id"]
                convObj["movieID"] = lineJson["meta"]["movie_id"]
                convObj["lines"] = [lineObj]
            else:
                convObj = conversations[lineJson["conversation_id"]]
                convObj["lines"].insert(0, lineObj)
            conversations[convObj["conversationID"]] = convObj

    return lines, conversations


# Extracts pairs of sentences from conversations
def extractSentencePairs(conversations):
    qa_pairs = []
    for conversation in conversations.values():
        # Iterate over all the lines of the conversation
        for i in range(len(conversation["lines"]) - 1):  # We ignore the last line (no answer for it)
            inputLine = conversation["lines"][i]["text"].strip()
            targetLine = conversation["lines"][i+1]["text"].strip()
            # Filter wrong samples (if one of the lists is empty)
            if inputLine and targetLine:
                qa_pairs.append([inputLine, targetLine])
    return qa_pairs

Now we’ll call these functions and create the file. We’ll call it formatted_movie_lines.txt.

# Define path to new file
datafile = os.path.join(corpus, "formatted_movie_lines.txt")

delimiter = '\t'
# Unescape the delimiter
delimiter = str(codecs.decode(delimiter, "unicode_escape"))

# Initialize lines dict and conversations dict
lines = {}
conversations = {}
# Load lines and conversations
print("\nProcessing corpus into lines and conversations...")
lines, conversations = loadLinesAndConversations(os.path.join(corpus, "utterances.jsonl"))

# Write new csv file
print("\nWriting newly formatted file...")
with open(datafile, 'w', encoding='utf-8') as outputfile:
    writer = csv.writer(outputfile, delimiter=delimiter, lineterminator='\n')
    for pair in extractSentencePairs(conversations):
        writer.writerow(pair)

# Print a sample of lines
print("\nSample lines from file:")
printLines(datafile)

Processing corpus into lines and conversations...

Writing newly formatted file...

Sample lines from file:
b'They do to!\tThey do not!\n'
b'She okay?\tI hope so.\n'
b"Wow\tLet's go.\n"
b'"I\'m kidding.  You know how sometimes you just become this ""persona""?  And you don\'t know how to quit?"\tNo\n'
b"No\tOkay -- you're gonna need to learn how to lie.\n"
b"I figured you'd get to the good stuff eventually.\tWhat good stuff?\n"
b'What good stuff?\t"The ""real you""."\n'
b'"The ""real you""."\tLike my fear of wearing pastels?\n'
b'do you listen to this crap?\tWhat crap?\n'
b"What crap?\tMe.  This endless ...blonde babble. I'm like, boring myself.\n"

Load and trim data

Our next order of business is to create a vocabulary and load query/response sentence pairs into memory.

Note that we are dealing with sequences of words, which do not have an implicit mapping to a discrete numerical space. Thus, we must create one by mapping each unique word that we encounter in our dataset to an index value.

For this we define a Voc class, which keeps a mapping from words to indexes, a reverse mapping of indexes to words, a count of each word and a total word count. The class provides methods for adding a word to the vocabulary (addWord), adding all words in a sentence (addSentence) and trimming infrequently seen words (trim). More on trimming later.

# Default word tokens
PAD_token = 0  # Used for padding short sentences
SOS_token = 1  # Start-of-sentence token
EOS_token = 2  # End-of-sentence token

class Voc:
    def __init__(self, name):
        self.name = name
        self.trimmed = False
        self.word2index = {}
        self.word2count = {}
        self.index2word = {PAD_token: "PAD", SOS_token: "SOS", EOS_token: "EOS"}
        self.num_words = 3  # Count SOS, EOS, PAD

    def addSentence(self, sentence):
        for word in sentence.split(' '):
            self.addWord(word)

    def addWord(self, word):
        if word not in self.word2index:
            self.word2index[word] = self.num_words
            self.word2count[word] = 1
            self.index2word[self.num_words] = word
            self.num_words += 1
        else:
            self.word2count[word] += 1

    # Remove words below a certain count threshold
    def trim(self, min_count):
        if self.trimmed:
            return
        self.trimmed = True

        keep_words = []

        for k, v in self.word2count.items():
            if v >= min_count:
                keep_words.append(k)

        print('keep_words {} / {} = {:.4f}'.format(
            len(keep_words), len(self.word2index), len(keep_words) / len(self.word2index)
        ))

        # Reinitialize dictionaries
        self.word2index = {}
        self.word2count = {}
        self.index2word = {PAD_token: "PAD", SOS_token: "SOS", EOS_token: "EOS"}
        self.num_words = 3 # Count default tokens

        for word in keep_words:
            self.addWord(word)

Now we can assemble our vocabulary and query/response sentence pairs. Before we are ready to use this data, we must perform some preprocessing.

First, we must convert the Unicode strings to ASCII using unicodeToAscii. Next, we should convert all letters to lowercase and trim all non-letter characters except for basic punctuation (normalizeString). Finally, to aid in training convergence, we will filter out sentences with length greater than the MAX_LENGTH threshold (filterPairs).

MAX_LENGTH = 10  # Maximum sentence length to consider

# Turn a Unicode string to plain ASCII, thanks to
# https://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
    )

# Lowercase, trim, and remove non-letter characters
def normalizeString(s):
    s = unicodeToAscii(s.lower().strip())
    s = re.sub(r"([.!?])", r" \1", s)
    s = re.sub(r"[^a-zA-Z.!?]+", r" ", s)
    s = re.sub(r"\s+", r" ", s).strip()
    return s

# Read query/response pairs and return a voc object
def readVocs(datafile, corpus_name):
    print("Reading lines...")
    # Read the file and split into lines
    lines = open(datafile, encoding='utf-8').\
        read().strip().split('\n')
    # Split every line into pairs and normalize
    pairs = [[normalizeString(s) for s in l.split('\t')] for l in lines]
    voc = Voc(corpus_name)
    return voc, pairs

# Returns True if both sentences in a pair 'p' are under the MAX_LENGTH threshold
def filterPair(p):
    # Input sequences need to preserve the last word for EOS token
    return len(p[0].split(' ')) < MAX_LENGTH and len(p[1].split(' ')) < MAX_LENGTH

# Filter pairs using the ``filterPair`` condition
def filterPairs(pairs):
    return [pair for pair in pairs if filterPair(pair)]

# Using the functions defined above, return a populated voc object and pairs list
def loadPrepareData(corpus, corpus_name, datafile, save_dir):
    print("Start preparing training data ...")
    voc, pairs = readVocs(datafile, corpus_name)
    print("Read {!s} sentence pairs".format(len(pairs)))
    pairs = filterPairs(pairs)
    print("Trimmed to {!s} sentence pairs".format(len(pairs)))
    print("Counting words...")
    for pair in pairs:
        voc.addSentence(pair[0])
        voc.addSentence(pair[1])
    print("Counted words:", voc.num_words)
    return voc, pairs


# Load/Assemble voc and pairs
save_dir = os.path.join("data", "save")
voc, pairs = loadPrepareData(corpus, corpus_name, datafile, save_dir)
# Print some pairs to validate
print("\npairs:")
for pair in pairs[:10]:
    print(pair)

Start preparing training data ...
Reading lines...
Read 221282 sentence pairs
Trimmed to 64313 sentence pairs
Counting words...
Counted words: 18082

pairs:
['they do to !', 'they do not !']
['she okay ?', 'i hope so .']
['wow', 'let s go .']
['what good stuff ?', 'the real you .']
['the real you .', 'like my fear of wearing pastels ?']
['do you listen to this crap ?', 'what crap ?']
['well no . . .', 'then that s all you had to say .']
['then that s all you had to say .', 'but']
['but', 'you always been this selfish ?']
['have fun tonight ?', 'tons']

Another tactic that is beneficial to achieving faster convergence during training is trimming rarely used words out of our vocabulary. Decreasing the feature space will also soften the difficulty of the function that the model must learn to approximate. We will do this as a two-step process:

1. Trim words used under MIN_COUNT threshold using the voc.trim function.

2. Filter out pairs with trimmed words.

MIN_COUNT = 3    # Minimum word count threshold for trimming

def trimRareWords(voc, pairs, MIN_COUNT):
    # Trim words used under the MIN_COUNT from the voc
    voc.trim(MIN_COUNT)
    # Filter out pairs with trimmed words
    keep_pairs = []
    for pair in pairs:
        input_sentence = pair[0]
        output_sentence = pair[1]
        keep_input = True
        keep_output = True
        # Check input sentence
        for word in input_sentence.split(' '):
            if word not in voc.word2index:
                keep_input = False
                break
        # Check output sentence
        for word in output_sentence.split(' '):
            if word not in voc.word2index:
                keep_output = False
                break

        # Only keep pairs that do not contain trimmed word(s) in their input or output sentence
        if keep_input and keep_output:
            keep_pairs.append(pair)

    print("Trimmed from {} pairs to {}, {:.4f} of total".format(len(pairs), len(keep_pairs), len(keep_pairs) / len(pairs)))
    return keep_pairs


# Trim voc and pairs
pairs = trimRareWords(voc, pairs, MIN_COUNT)

keep_words 7833 / 18079 = 0.4333
Trimmed from 64313 pairs to 53131, 0.8261 of total

Prepare Data for Models

Although we have put a great deal of effort into preparing and massaging our data into a nice vocabulary object and list of sentence pairs, our models will ultimately expect numerical torch tensors as inputs. One way to prepare the processed data for the models can be found in the seq2seq translation tutorial. In that tutorial, we use a batch size of 1, meaning that all we have to do is convert the words in our sentence pairs to their corresponding indexes from the vocabulary and feed this to the models.

However, if you’re interested in speeding up training and/or would like to leverage GPU parallelization capabilities, you will need to train with mini-batches.

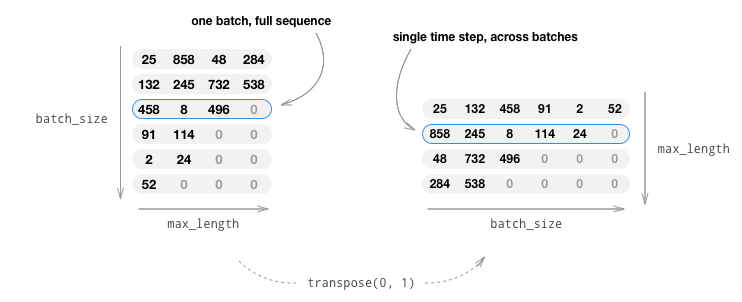
Using mini-batches also means that we must be mindful of the variation of sentence length in our batches. To accommodate sentences of different sizes in the same batch, we will make our batched input tensor of shape (max_length, batch_size), where sentences shorter than the max_length are zero padded after an EOS_token.

If we simply convert our English sentences to tensors by converting words to their indexes(indexesFromSentence) and zero-pad, our tensor would have shape (batch_size, max_length) and indexing the first dimension would return a full sequence across all time-steps. However, we need to be able to index our batch along time, and across all sequences in the batch. Therefore, we transpose our input batch shape to (max_length, batch_size), so that indexing across the first dimension returns a time step across all sentences in the batch. We handle this transpose implicitly in the zeroPadding function.

The inputVar function handles the process of converting sentences to tensor, ultimately creating a correctly shaped zero-padded tensor. It also returns a tensor of lengths for each of the sequences in the batch which will be passed to our decoder later.

The outputVar function performs a similar function to inputVar, but instead of returning a lengths tensor, it returns a binary mask tensor and a maximum target sentence length. The binary mask tensor has the same shape as the output target tensor, but every element that is a PAD_token is 0 and all others are 1.

batch2TrainData simply takes a bunch of pairs and returns the input and target tensors using the aforementioned functions.

def indexesFromSentence(voc, sentence):
    return [voc.word2index[word] for word in sentence.split(' ')] + [EOS_token]


def zeroPadding(l, fillvalue=PAD_token):
    return list(itertools.zip_longest(*l, fillvalue=fillvalue))

def binaryMatrix(l, value=PAD_token):
    m = []
    for i, seq in enumerate(l):
        m.append([])
        for token in seq:
            if token == PAD_token:
                m[i].append(0)
            else:
                m[i].append(1)
    return m

# Returns padded input sequence tensor and lengths
def inputVar(l, voc):
    indexes_batch = [indexesFromSentence(voc, sentence) for sentence in l]
    lengths = torch.tensor([len(indexes) for indexes in indexes_batch])
    padList = zeroPadding(indexes_batch)
    padVar = torch.LongTensor(padList)
    return padVar, lengths

# Returns padded target sequence tensor, padding mask, and max target length
def outputVar(l, voc):
    indexes_batch = [indexesFromSentence(voc, sentence) for sentence in l]
    max_target_len = max([len(indexes) for indexes in indexes_batch])
    padList = zeroPadding(indexes_batch)
    mask = binaryMatrix(padList)
    mask = torch.BoolTensor(mask)
    padVar = torch.LongTensor(padList)
    return padVar, mask, max_target_len

# Returns all items for a given batch of pairs
def batch2TrainData(voc, pair_batch):
    pair_batch.sort(key=lambda x: len(x[0].split(" ")), reverse=True)
    input_batch, output_batch = [], []
    for pair in pair_batch:
        input_batch.append(pair[0])
        output_batch.append(pair[1])
    inp, lengths = inputVar(input_batch, voc)
    output, mask, max_target_len = outputVar(output_batch, voc)
    return inp, lengths, output, mask, max_target_len


# Example for validation
small_batch_size = 5
batches = batch2TrainData(voc, [random.choice(pairs) for _ in range(small_batch_size)])
input_variable, lengths, target_variable, mask, max_target_len = batches

print("input_variable:", input_variable)
print("lengths:", lengths)
print("target_variable:", target_variable)
print("mask:", mask)
print("max_target_len:", max_target_len)

input_variable: tensor([[5503,  111,  128,   62, 2104],
        [  50,   11,  665,  201,    6],
        [  64,  311,  223,   14,    2],
        [ 514,   24,   10,    2,    0],
        [ 101,   62,    2,    0,    0],
        [  24,  647,    0,    0,    0],
        [ 112,   10,    0,    0,    0],
        [  14,    2,    0,    0,    0],
        [   2,    0,    0,    0,    0]])
lengths: tensor([9, 8, 5, 4, 3])
target_variable: tensor([[ 104,  146,   97,  762, 2104],
        [ 148,   14,  102,   62,    6],
        [  72,    2,   14,  201,    2],
        [  14,    0,    2,   14,    0],
        [   2,    0,    0,   24,    0],
        [   0,    0,    0, 1924,    0],
        [   0,    0,    0,    5,    0],
        [   0,    0,    0,   72,    0],
        [   0,    0,    0,   14,    0],
        [   0,    0,    0,    2,    0]])
mask: tensor([[ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True, False,  True,  True, False],
        [ True, False, False,  True, False],
        [False, False, False,  True, False],
        [False, False, False,  True, False],
        [False, False, False,  True, False],
        [False, False, False,  True, False],
        [False, False, False,  True, False]])
max_target_len: 10

Define Models

Seq2Seq Model

The brains of our chatbot is a sequence-to-sequence (seq2seq) model. The goal of a seq2seq model is to take a variable-length sequence as an input, and return a variable-length sequence as an output using a fixed-sized model.

Sutskever et al. discovered that by using two separate recurrent neural nets together, we can accomplish this task. One RNN acts as an encoder, which encodes a variable length input sequence to a fixed-length context vector. In theory, this context vector (the final hidden layer of the RNN) will contain semantic information about the query sentence that is input to the bot. The second RNN is a decoder, which takes an input word and the context vector, and returns a guess for the next word in the sequence and a hidden state to use in the next iteration.

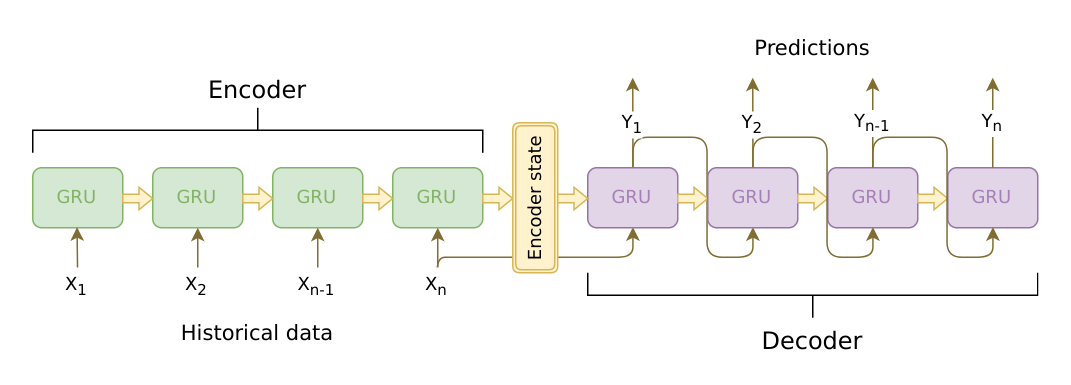
Image source: https://jeddy92.github.io/JEddy92.github.io/ts_seq2seq_intro/

Encoder

The encoder RNN iterates through the input sentence one token (e.g. word) at a time, at each time step outputting an “output” vector and a “hidden state” vector. The hidden state vector is then passed to the next time step, while the output vector is recorded. The encoder transforms the context it saw at each point in the sequence into a set of points in a high-dimensional space, which the decoder will use to generate a meaningful output for the given task.

At the heart of our encoder is a multi-layered Gated Recurrent Unit, invented by Cho et al. in 2014. We will use a bidirectional variant of the GRU, meaning that there are essentially two independent RNNs: one that is fed the input sequence in normal sequential order, and one that is fed the input sequence in reverse order. The outputs of each network are summed at each time step. Using a bidirectional GRU will give us the advantage of encoding both past and future contexts.

Bidirectional RNN:

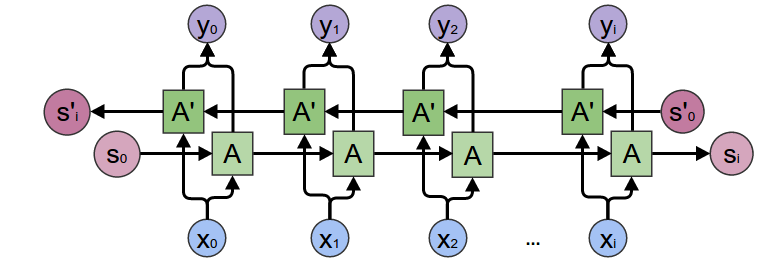
Image source: https://colah.github.io/posts/2015-09-NN-Types-FP/

Note that an embedding layer is used to encode our word indices in an arbitrarily sized feature space. For our models, this layer will map each word to a feature space of size hidden_size. When trained, these values should encode semantic similarity between similar meaning words.

Finally, if passing a padded batch of sequences to an RNN module, we must pack and unpack padding around the RNN pass using nn.utils.rnn.pack_padded_sequence and nn.utils.rnn.pad_packed_sequence respectively.

Computation Graph:

1. Convert word indexes to embeddings.

2. Pack padded batch of sequences for RNN module.

3. Forward pass through GRU.

4. Unpack padding.

5. Sum bidirectional GRU outputs.

6. Return output and final hidden state.

Inputs:

• input_seq: batch of input sentences; shape=(max_length, batch_size)

• input_lengths: list of sentence lengths corresponding to each sentence in the batch; shape=(batch_size)

• hidden: hidden state; shape=(n_layers x num_directions, batch_size, hidden_size)

Outputs:

• outputs: output features from the last hidden layer of the GRU (sum of bidirectional outputs); shape=(max_length, batch_size, hidden_size)

• hidden: updated hidden state from GRU; shape=(n_layers x num_directions, batch_size, hidden_size)

class EncoderRNN(nn.Module):
    def __init__(self, hidden_size, embedding, n_layers=1, dropout=0):
        super(EncoderRNN, self).__init__()
        self.n_layers = n_layers
        self.hidden_size = hidden_size
        self.embedding = embedding

        # Initialize GRU; the input_size and hidden_size parameters are both set to 'hidden_size'
        #   because our input size is a word embedding with number of features == hidden_size
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers,
                          dropout=(0 if n_layers == 1 else dropout), bidirectional=True)

    def forward(self, input_seq, input_lengths, hidden=None):
        # Convert word indexes to embeddings
        embedded = self.embedding(input_seq)
        # Pack padded batch of sequences for RNN module
        packed = nn.utils.rnn.pack_padded_sequence(embedded, input_lengths)
        # Forward pass through GRU
        outputs, hidden = self.gru(packed, hidden)
        # Unpack padding
        outputs, _ = nn.utils.rnn.pad_packed_sequence(outputs)
        # Sum bidirectional GRU outputs
        outputs = outputs[:, :, :self.hidden_size] + outputs[:, : ,self.hidden_size:]
        # Return output and final hidden state
        return outputs, hidden

Decoder

The decoder RNN generates the response sentence in a token-by-token fashion. It uses the encoder’s context vectors, and internal hidden states to generate the next word in the sequence. It continues generating words until it outputs an EOS_token, representing the end of the sentence. A common problem with a vanilla seq2seq decoder is that if we rely solely on the context vector to encode the entire input sequence’s meaning, it is likely that we will have information loss. This is especially the case when dealing with long input sequences, greatly limiting the capability of our decoder.

To combat this, Bahdanau et al. created an “attention mechanism” that allows the decoder to pay attention to certain parts of the input sequence, rather than using the entire fixed context at every step.

At a high level, attention is calculated using the decoder’s current hidden state and the encoder’s outputs. The output attention weights have the same shape as the input sequence, allowing us to multiply them by the encoder outputs, giving us a weighted sum which indicates the parts of encoder output to pay attention to. Sean Robertson’s figure describes this very well:

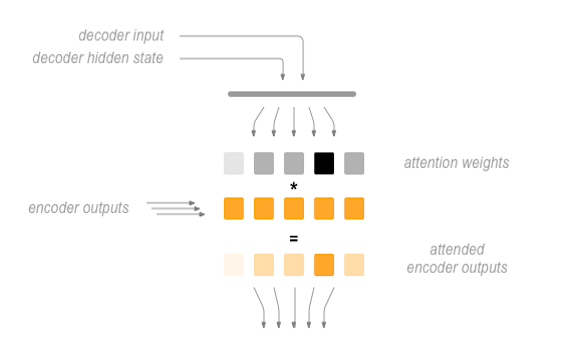
Luong et al. improved upon Bahdanau et al.’s groundwork by creating “Global attention”. The key difference is that with “Global attention”, we consider all of the encoder’s hidden states, as opposed to Bahdanau et al.’s “Local attention”, which only considers the encoder’s hidden state from the current time step. Another difference is that with “Global attention”, we calculate attention weights, or energies, using the hidden state of the decoder from the current time step only. Bahdanau et al.’s attention calculation requires knowledge of the decoder’s state from the previous time step. Also, Luong et al. provides various methods to calculate the attention energies between the encoder output and decoder output which are called “score functions”:

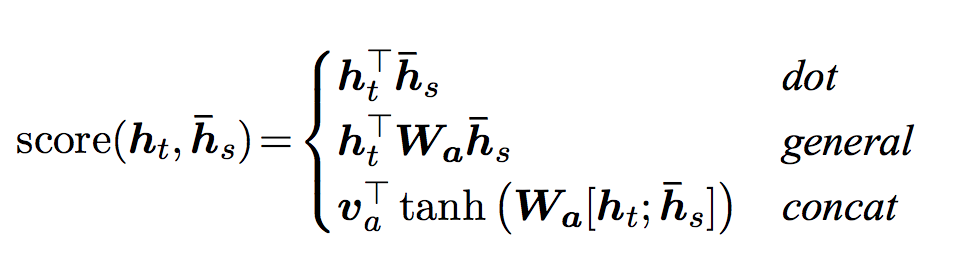
where \(h_t\) = current target decoder state and \(\bar{h}_s\) = all encoder states.

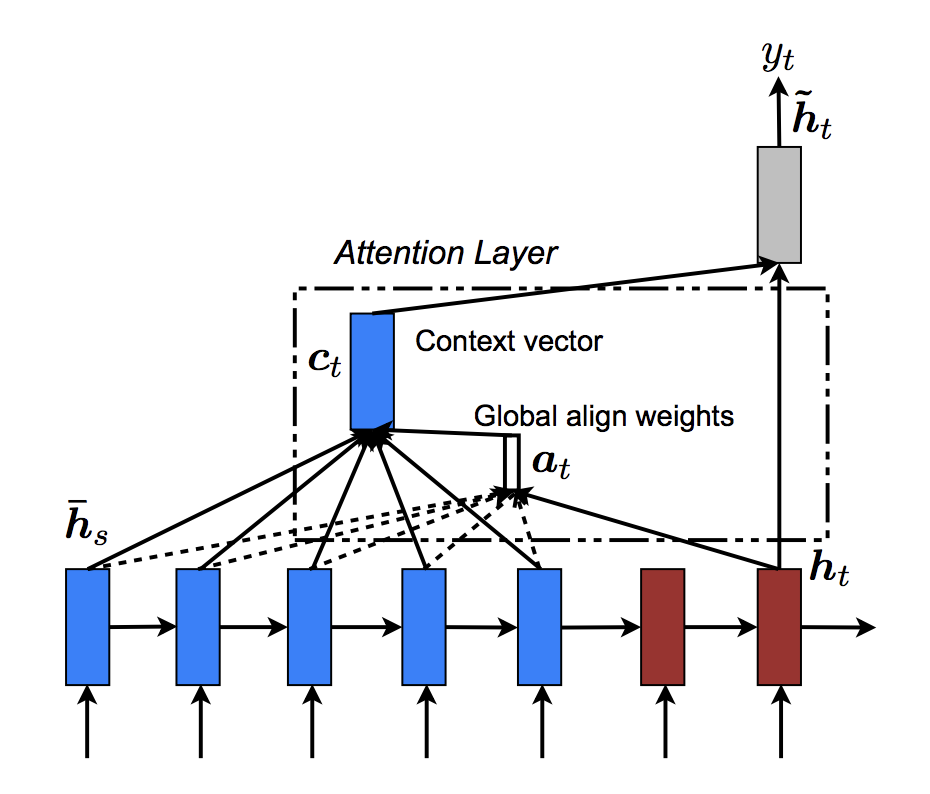
Overall, the Global attention mechanism can be summarized by the following figure. Note that we will implement the “Attention Layer” as a separate nn.Module called Attn. The output of this module is a softmax normalized weights tensor of shape (batch_size, 1, max_length).

# Luong attention layer
class Attn(nn.Module):
    def __init__(self, method, hidden_size):
        super(Attn, self).__init__()
        self.method = method
        if self.method not in ['dot', 'general', 'concat']:
            raise ValueError(self.method, "is not an appropriate attention method.")
        self.hidden_size = hidden_size
        if self.method == 'general':
            self.attn = nn.Linear(self.hidden_size, hidden_size)
        elif self.method == 'concat':
            self.attn = nn.Linear(self.hidden_size * 2, hidden_size)
            self.v = nn.Parameter(torch.FloatTensor(hidden_size))

    def dot_score(self, hidden, encoder_output):
        return torch.sum(hidden * encoder_output, dim=2)

    def general_score(self, hidden, encoder_output):
        energy = self.attn(encoder_output)
        return torch.sum(hidden * energy, dim=2)

    def concat_score(self, hidden, encoder_output):
        energy = self.attn(torch.cat((hidden.expand(encoder_output.size(0), -1, -1), encoder_output), 2)).tanh()
        return torch.sum(self.v * energy, dim=2)

    def forward(self, hidden, encoder_outputs):
        # Calculate the attention weights (energies) based on the given method
        if self.method == 'general':
            attn_energies = self.general_score(hidden, encoder_outputs)
        elif self.method == 'concat':
            attn_energies = self.concat_score(hidden, encoder_outputs)
        elif self.method == 'dot':
            attn_energies = self.dot_score(hidden, encoder_outputs)

        # Transpose max_length and batch_size dimensions
        attn_energies = attn_energies.t()

        # Return the softmax normalized probability scores (with added dimension)
        return F.softmax(attn_energies, dim=1).unsqueeze(1)

Now that we have defined our attention submodule, we can implement the actual decoder model. For the decoder, we will manually feed our batch one time step at a time. This means that our embedded word tensor and GRU output will both have shape (1, batch_size, hidden_size).

Computation Graph:

1. Get embedding of current input word.

2. Forward through unidirectional GRU.

3. Calculate attention weights from the current GRU output from (2).

4. Multiply attention weights to encoder outputs to get new “weighted sum” context vector.

5. Concatenate weighted context vector and GRU output using Luong eq. 5.

6. Predict next word using Luong eq. 6 (without softmax).

7. Return output and final hidden state.

Inputs:

• input_step: one time step (one word) of input sequence batch; shape=(1, batch_size)

• last_hidden: final hidden layer of GRU; shape=(n_layers x num_directions, batch_size, hidden_size)

• encoder_outputs: encoder model’s output; shape=(max_length, batch_size, hidden_size)

Outputs:

• output: softmax normalized tensor giving probabilities of each word being the correct next word in the decoded sequence; shape=(batch_size, voc.num_words)

• hidden: final hidden state of GRU; shape=(n_layers x num_directions, batch_size, hidden_size)

class LuongAttnDecoderRNN(nn.Module):
    def __init__(self, attn_model, embedding, hidden_size, output_size, n_layers=1, dropout=0.1):
        super(LuongAttnDecoderRNN, self).__init__()

        # Keep for reference
        self.attn_model = attn_model
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.n_layers = n_layers
        self.dropout = dropout

        # Define layers
        self.embedding = embedding
        self.embedding_dropout = nn.Dropout(dropout)
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers, dropout=(0 if n_layers == 1 else dropout))
        self.concat = nn.Linear(hidden_size * 2, hidden_size)
        self.out = nn.Linear(hidden_size, output_size)

        self.attn = Attn(attn_model, hidden_size)

    def forward(self, input_step, last_hidden, encoder_outputs):
        # Note: we run this one step (word) at a time
        # Get embedding of current input word
        embedded = self.embedding(input_step)
        embedded = self.embedding_dropout(embedded)
        # Forward through unidirectional GRU
        rnn_output, hidden = self.gru(embedded, last_hidden)
        # Calculate attention weights from the current GRU output
        attn_weights = self.attn(rnn_output, encoder_outputs)
        # Multiply attention weights to encoder outputs to get new "weighted sum" context vector
        context = attn_weights.bmm(encoder_outputs.transpose(0, 1))
        # Concatenate weighted context vector and GRU output using Luong eq. 5
        rnn_output = rnn_output.squeeze(0)
        context = context.squeeze(1)
        concat_input = torch.cat((rnn_output, context), 1)
        concat_output = torch.tanh(self.concat(concat_input))
        # Predict next word using Luong eq. 6
        output = self.out(concat_output)
        output = F.softmax(output, dim=1)
        # Return output and final hidden state
        return output, hidden

Define Training Procedure

Masked loss

Since we are dealing with batches of padded sequences, we cannot simply consider all elements of the tensor when calculating loss. We define maskNLLLoss to calculate our loss based on our decoder’s output tensor, the target tensor, and a binary mask tensor describing the padding of the target tensor. This loss function calculates the average negative log likelihood of the elements that correspond to a 1 in the mask tensor.

def maskNLLLoss(inp, target, mask):
    nTotal = mask.sum()
    crossEntropy = -torch.log(torch.gather(inp, 1, target.view(-1, 1)).squeeze(1))
    loss = crossEntropy.masked_select(mask).mean()
    loss = loss.to(device)
    return loss, nTotal.item()

Single training iteration

The train function contains the algorithm for a single training iteration (a single batch of inputs).

We will use a couple of clever tricks to aid in convergence:

• The first trick is using teacher forcing. This means that at some probability, set by teacher_forcing_ratio, we use the current target word as the decoder’s next input rather than using the decoder’s current guess. This technique acts as training wheels for the decoder, aiding in more efficient training. However, teacher forcing can lead to model instability during inference, as the decoder may not have a sufficient chance to truly craft its own output sequences during training. Thus, we must be mindful of how we are setting the teacher_forcing_ratio, and not be fooled by fast convergence.

• The second trick that we implement is gradient clipping. This is a commonly used technique for countering the “exploding gradient” problem. In essence, by clipping or thresholding gradients to a maximum value, we prevent the gradients from growing exponentially and either overflow (NaN), or overshoot steep cliffs in the cost function.

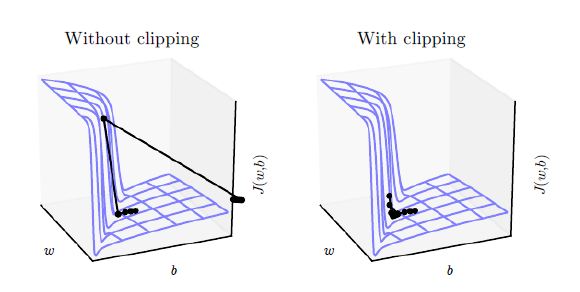
Image source: Goodfellow et al. Deep Learning. 2016. https://www.deeplearningbook.org/

Sequence of Operations:

1. Forward pass entire input batch through encoder.

2. Initialize decoder inputs as SOS_token, and hidden state as the encoder’s final hidden state.

3. Forward input batch sequence through decoder one time step at a time.

4. If teacher forcing: set next decoder input as the current target; else: set next decoder input as current decoder output.

5. Calculate and accumulate loss.

6. Perform backpropagation.

7. Clip gradients.

8. Update encoder and decoder model parameters.

Note

PyTorch’s RNN modules (RNN, LSTM, GRU) can be used like any other non-recurrent layers by simply passing them the entire input sequence (or batch of sequences). We use the GRU layer like this in the encoder. The reality is that under the hood, there is an iterative process looping over each time step calculating hidden states. Alternatively, you can run these modules one time-step at a time. In this case, we manually loop over the sequences during the training process like we must do for the decoder model. As long as you maintain the correct conceptual model of these modules, implementing sequential models can be very straightforward.

def train(input_variable, lengths, target_variable, mask, max_target_len, encoder, decoder, embedding,
          encoder_optimizer, decoder_optimizer, batch_size, clip, max_length=MAX_LENGTH):

    # Zero gradients
    encoder_optimizer.zero_grad()
    decoder_optimizer.zero_grad()

    # Set device options
    input_variable = input_variable.to(device)
    target_variable = target_variable.to(device)
    mask = mask.to(device)
    # Lengths for RNN packing should always be on the CPU
    lengths = lengths.to("cpu")

    # Initialize variables
    loss = 0
    print_losses = []
    n_totals = 0

    # Forward pass through encoder
    encoder_outputs, encoder_hidden = encoder(input_variable, lengths)

    # Create initial decoder input (start with SOS tokens for each sentence)
    decoder_input = torch.LongTensor([[SOS_token for _ in range(batch_size)]])
    decoder_input = decoder_input.to(device)

    # Set initial decoder hidden state to the encoder's final hidden state
    decoder_hidden = encoder_hidden[:decoder.n_layers]

    # Determine if we are using teacher forcing this iteration
    use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False

    # Forward batch of sequences through decoder one time step at a time
    if use_teacher_forcing:
        for t in range(max_target_len):
            decoder_output, decoder_hidden = decoder(
                decoder_input, decoder_hidden, encoder_outputs
            )
            # Teacher forcing: next input is current target
            decoder_input = target_variable[t].view(1, -1)
            # Calculate and accumulate loss
            mask_loss, nTotal = maskNLLLoss(decoder_output, target_variable[t], mask[t])
            loss += mask_loss
            print_losses.append(mask_loss.item() * nTotal)
            n_totals += nTotal
    else:
        for t in range(max_target_len):
            decoder_output, decoder_hidden = decoder(
                decoder_input, decoder_hidden, encoder_outputs
            )
            # No teacher forcing: next input is decoder's own current output
            _, topi = decoder_output.topk(1)
            decoder_input = torch.LongTensor([[topi[i][0] for i in range(batch_size)]])
            decoder_input = decoder_input.to(device)
            # Calculate and accumulate loss
            mask_loss, nTotal = maskNLLLoss(decoder_output, target_variable[t], mask[t])
            loss += mask_loss
            print_losses.append(mask_loss.item() * nTotal)
            n_totals += nTotal

    # Perform backpropagation
    loss.backward()

    # Clip gradients: gradients are modified in place
    _ = nn.utils.clip_grad_norm_(encoder.parameters(), clip)
    _ = nn.utils.clip_grad_norm_(decoder.parameters(), clip)

    # Adjust model weights
    encoder_optimizer.step()
    decoder_optimizer.step()

    return sum(print_losses) / n_totals

Training iterations

It is finally time to tie the full training procedure together with the data. The trainIters function is responsible for running n_iterations of training given the passed models, optimizers, data, etc. This function is quite self explanatory, as we have done the heavy lifting with the train function.

One thing to note is that when we save our model, we save a tarball containing the encoder and decoder state_dicts (parameters), the optimizers’ state_dicts, the loss, the iteration, etc. Saving the model in this way will give us the ultimate flexibility with the checkpoint. After loading a checkpoint, we will be able to use the model parameters to run inference, or we can continue training right where we left off.

def trainIters(model_name, voc, pairs, encoder, decoder, encoder_optimizer, decoder_optimizer, embedding, encoder_n_layers, decoder_n_layers, save_dir, n_iteration, batch_size, print_every, save_every, clip, corpus_name, loadFilename):

    # Load batches for each iteration
    training_batches = [batch2TrainData(voc, [random.choice(pairs) for _ in range(batch_size)])
                      for _ in range(n_iteration)]

    # Initializations
    print('Initializing ...')
    start_iteration = 1
    print_loss = 0
    if loadFilename:
        start_iteration = checkpoint['iteration'] + 1

    # Training loop
    print("Training...")
    for iteration in range(start_iteration, n_iteration + 1):
        training_batch = training_batches[iteration - 1]
        # Extract fields from batch
        input_variable, lengths, target_variable, mask, max_target_len = training_batch

        # Run a training iteration with batch
        loss = train(input_variable, lengths, target_variable, mask, max_target_len, encoder,
                     decoder, embedding, encoder_optimizer, decoder_optimizer, batch_size, clip)
        print_loss += loss

        # Print progress
        if iteration % print_every == 0:
            print_loss_avg = print_loss / print_every
            print("Iteration: {}; Percent complete: {:.1f}%; Average loss: {:.4f}".format(iteration, iteration / n_iteration * 100, print_loss_avg))
            print_loss = 0

        # Save checkpoint
        if (iteration % save_every == 0):
            directory = os.path.join(save_dir, model_name, corpus_name, '{}-{}_{}'.format(encoder_n_layers, decoder_n_layers, hidden_size))
            if not os.path.exists(directory):
                os.makedirs(directory)
            torch.save({
                'iteration': iteration,
                'en': encoder.state_dict(),
                'de': decoder.state_dict(),
                'en_opt': encoder_optimizer.state_dict(),
                'de_opt': decoder_optimizer.state_dict(),
                'loss': loss,
                'voc_dict': voc.__dict__,
                'embedding': embedding.state_dict()
            }, os.path.join(directory, '{}_{}.tar'.format(iteration, 'checkpoint')))

Define Evaluation

After training a model, we want to be able to talk to the bot ourselves. First, we must define how we want the model to decode the encoded input.

Greedy decoding

Greedy decoding is the decoding method that we use during training when we are NOT using teacher forcing. In other words, for each time step, we simply choose the word from decoder_output with the highest softmax value. This decoding method is optimal on a single time-step level.

To facilitate the greedy decoding operation, we define a GreedySearchDecoder class. When run, an object of this class takes an input sequence (input_seq) of shape (input_seq length, 1), a scalar input length (input_length) tensor, and a max_length to bound the response sentence length. The input sentence is evaluated using the following computational graph:

Computation Graph:

1. Forward input through encoder model.

2. Prepare encoder’s final hidden layer to be first hidden input to the decoder.

3. Initialize decoder’s first input as SOS_token.

4. Initialize tensors to append decoded words to.

5. Iteratively decode one word token at a time:

   1. Forward pass through decoder.

   2. Obtain most likely word token and its softmax score.

   3. Record token and score.

   4. Prepare current token to be next decoder input.

6. Return collections of word tokens and scores.

class GreedySearchDecoder(nn.Module):
    def __init__(self, encoder, decoder):
        super(GreedySearchDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, input_seq, input_length, max_length):
        # Forward input through encoder model
        encoder_outputs, encoder_hidden = self.encoder(input_seq, input_length)
        # Prepare encoder's final hidden layer to be first hidden input to the decoder
        decoder_hidden = encoder_hidden[:self.decoder.n_layers]
        # Initialize decoder input with SOS_token
        decoder_input = torch.ones(1, 1, device=device, dtype=torch.long) * SOS_token
        # Initialize tensors to append decoded words to
        all_tokens = torch.zeros([0], device=device, dtype=torch.long)
        all_scores = torch.zeros([0], device=device)
        # Iteratively decode one word token at a time
        for _ in range(max_length):
            # Forward pass through decoder
            decoder_output, decoder_hidden = self.decoder(decoder_input, decoder_hidden, encoder_outputs)
            # Obtain most likely word token and its softmax score
            decoder_scores, decoder_input = torch.max(decoder_output, dim=1)
            # Record token and score
            all_tokens = torch.cat((all_tokens, decoder_input), dim=0)
            all_scores = torch.cat((all_scores, decoder_scores), dim=0)
            # Prepare current token to be next decoder input (add a dimension)
            decoder_input = torch.unsqueeze(decoder_input, 0)
        # Return collections of word tokens and scores
        return all_tokens, all_scores

Evaluate my text

Now that we have our decoding method defined, we can write functions for evaluating a string input sentence. The evaluate function manages the low-level process of handling the input sentence. We first format the sentence as an input batch of word indexes with batch_size==1. We do this by converting the words of the sentence to their corresponding indexes, and transposing the dimensions to prepare the tensor for our models. We also create a lengths tensor which contains the length of our input sentence. In this case, lengths is scalar because we are only evaluating one sentence at a time (batch_size==1). Next, we obtain the decoded response sentence tensor using our GreedySearchDecoder object (searcher). Finally, we convert the response’s indexes to words and return the list of decoded words.

evaluateInput acts as the user interface for our chatbot. When called, an input text field will spawn in which we can enter our query sentence. After typing our input sentence and pressing Enter, our text is normalized in the same way as our training data, and is ultimately fed to the evaluate function to obtain a decoded output sentence. We loop this process, so we can keep chatting with our bot until we enter either “q” or “quit”.

Finally, if a sentence is entered that contains a word that is not in the vocabulary, we handle this gracefully by printing an error message and prompting the user to enter another sentence.

def evaluate(encoder, decoder, searcher, voc, sentence, max_length=MAX_LENGTH):
    ### Format input sentence as a batch
    # words -> indexes
    indexes_batch = [indexesFromSentence(voc, sentence)]
    # Create lengths tensor
    lengths = torch.tensor([len(indexes) for indexes in indexes_batch])
    # Transpose dimensions of batch to match models' expectations
    input_batch = torch.LongTensor(indexes_batch).transpose(0, 1)
    # Use appropriate device
    input_batch = input_batch.to(device)
    lengths = lengths.to("cpu")
    # Decode sentence with searcher
    tokens, scores = searcher(input_batch, lengths, max_length)
    # indexes -> words
    decoded_words = [voc.index2word[token.item()] for token in tokens]
    return decoded_words


def evaluateInput(encoder, decoder, searcher, voc):
    input_sentence = ''
    while(1):
        try:
            # Get input sentence
            input_sentence = input('> ')
            # Check if it is quit case
            if input_sentence == 'q' or input_sentence == 'quit': break
            # Normalize sentence
            input_sentence = normalizeString(input_sentence)
            # Evaluate sentence
            output_words = evaluate(encoder, decoder, searcher, voc, input_sentence)
            # Format and print response sentence
            output_words[:] = [x for x in output_words if not (x == 'EOS' or x == 'PAD')]
            print('Bot:', ' '.join(output_words))

        except KeyError:
            print("Error: Encountered unknown word.")

Run Model

Finally, it is time to run our model!

Regardless of whether we want to train or test the chatbot model, we must initialize the individual encoder and decoder models. In the following block, we set our desired configurations, choose to start from scratch or set a checkpoint to load from, and build and initialize the models. Feel free to play with different model configurations to optimize performance.

# Configure models
model_name = 'cb_model'
attn_model = 'dot'
#``attn_model = 'general'``
#``attn_model = 'concat'``
hidden_size = 500
encoder_n_layers = 2
decoder_n_layers = 2
dropout = 0.1
batch_size = 64

# Set checkpoint to load from; set to None if starting from scratch
loadFilename = None
checkpoint_iter = 4000

Sample code to load from a checkpoint:

loadFilename = os.path.join(save_dir, model_name, corpus_name,
                    '{}-{}_{}'.format(encoder_n_layers, decoder_n_layers, hidden_size),
                    '{}_checkpoint.tar'.format(checkpoint_iter))

# Load model if a ``loadFilename`` is provided
if loadFilename:
    # If loading on same machine the model was trained on
    checkpoint = torch.load(loadFilename)
    # If loading a model trained on GPU to CPU
    #checkpoint = torch.load(loadFilename, map_location=torch.device('cpu'))
    encoder_sd = checkpoint['en']
    decoder_sd = checkpoint['de']
    encoder_optimizer_sd = checkpoint['en_opt']
    decoder_optimizer_sd = checkpoint['de_opt']
    embedding_sd = checkpoint['embedding']
    voc.__dict__ = checkpoint['voc_dict']


print('Building encoder and decoder ...')
# Initialize word embeddings
embedding = nn.Embedding(voc.num_words, hidden_size)
if loadFilename:
    embedding.load_state_dict(embedding_sd)
# Initialize encoder & decoder models
encoder = EncoderRNN(hidden_size, embedding, encoder_n_layers, dropout)
decoder = LuongAttnDecoderRNN(attn_model, embedding, hidden_size, voc.num_words, decoder_n_layers, dropout)
if loadFilename:
    encoder.load_state_dict(encoder_sd)
    decoder.load_state_dict(decoder_sd)
# Use appropriate device
encoder = encoder.to(device)
decoder = decoder.to(device)
print('Models built and ready to go!')

Building encoder and decoder ...
Models built and ready to go!

Run Training

Run the following block if you want to train the model.

First we set training parameters, then we initialize our optimizers, and finally we call the trainIters function to run our training iterations.

# Configure training/optimization
clip = 50.0
teacher_forcing_ratio = 1.0
learning_rate = 0.0001
decoder_learning_ratio = 5.0
n_iteration = 4000
print_every = 1
save_every = 500

# Ensure dropout layers are in train mode
encoder.train()
decoder.train()

# Initialize optimizers
print('Building optimizers ...')
encoder_optimizer = optim.Adam(encoder.parameters(), lr=learning_rate)
decoder_optimizer = optim.Adam(decoder.parameters(), lr=learning_rate * decoder_learning_ratio)
if loadFilename:
    encoder_optimizer.load_state_dict(encoder_optimizer_sd)
    decoder_optimizer.load_state_dict(decoder_optimizer_sd)

# If you have an accelerator, configure it to call
for state in encoder_optimizer.state.values():
    for k, v in state.items():
        if isinstance(v, torch.Tensor):
            state[k] = v.to(device)

for state in decoder_optimizer.state.values():
    for k, v in state.items():
        if isinstance(v, torch.Tensor):
            state[k] = v.to(device)

# Run training iterations
print("Starting Training!")
trainIters(model_name, voc, pairs, encoder, decoder, encoder_optimizer, decoder_optimizer,
           embedding, encoder_n_layers, decoder_n_layers, save_dir, n_iteration, batch_size,
           print_every, save_every, clip, corpus_name, loadFilename)

Building optimizers ...
Starting Training!
Initializing ...
Training...
Iteration: 1; Percent complete: 0.0%; Average loss: 8.9769
Iteration: 2; Percent complete: 0.1%; Average loss: 8.8705
Iteration: 3; Percent complete: 0.1%; Average loss: 8.6787
Iteration: 4; Percent complete: 0.1%; Average loss: 8.4050
Iteration: 5; Percent complete: 0.1%; Average loss: 7.9538
Iteration: 6; Percent complete: 0.1%; Average loss: 7.5169
Iteration: 7; Percent complete: 0.2%; Average loss: 6.8187
Iteration: 8; Percent complete: 0.2%; Average loss: 6.8553
Iteration: 9; Percent complete: 0.2%; Average loss: 6.6652
Iteration: 10; Percent complete: 0.2%; Average loss: 6.5194
Iteration: 11; Percent complete: 0.3%; Average loss: 6.4057
Iteration: 12; Percent complete: 0.3%; Average loss: 6.0596
Iteration: 13; Percent complete: 0.3%; Average loss: 5.5799
Iteration: 14; Percent complete: 0.4%; Average loss: 5.5310
Iteration: 15; Percent complete: 0.4%; Average loss: 5.8394
Iteration: 16; Percent complete: 0.4%; Average loss: 5.5019
Iteration: 17; Percent complete: 0.4%; Average loss: 5.2380
Iteration: 18; Percent complete: 0.4%; Average loss: 4.9685
Iteration: 19; Percent complete: 0.5%; Average loss: 4.9826
Iteration: 20; Percent complete: 0.5%; Average loss: 4.8777
Iteration: 21; Percent complete: 0.5%; Average loss: 4.9823
Iteration: 22; Percent complete: 0.5%; Average loss: 4.8242
Iteration: 23; Percent complete: 0.6%; Average loss: 4.8575
Iteration: 24; Percent complete: 0.6%; Average loss: 5.0019
Iteration: 25; Percent complete: 0.6%; Average loss: 4.9155
Iteration: 26; Percent complete: 0.7%; Average loss: 4.7596
Iteration: 27; Percent complete: 0.7%; Average loss: 4.8192
Iteration: 28; Percent complete: 0.7%; Average loss: 4.6436
Iteration: 29; Percent complete: 0.7%; Average loss: 5.0367
Iteration: 30; Percent complete: 0.8%; Average loss: 4.4735
Iteration: 31; Percent complete: 0.8%; Average loss: 4.7764
Iteration: 32; Percent complete: 0.8%; Average loss: 4.9370
Iteration: 33; Percent complete: 0.8%; Average loss: 4.9770
Iteration: 34; Percent complete: 0.9%; Average loss: 4.8575
Iteration: 35; Percent complete: 0.9%; Average loss: 4.5935
Iteration: 36; Percent complete: 0.9%; Average loss: 4.5851
Iteration: 37; Percent complete: 0.9%; Average loss: 4.7199
Iteration: 38; Percent complete: 0.9%; Average loss: 4.7052
Iteration: 39; Percent complete: 1.0%; Average loss: 4.6335
Iteration: 40; Percent complete: 1.0%; Average loss: 4.7965
Iteration: 41; Percent complete: 1.0%; Average loss: 4.7232
Iteration: 42; Percent complete: 1.1%; Average loss: 4.4699
Iteration: 43; Percent complete: 1.1%; Average loss: 4.5483
Iteration: 44; Percent complete: 1.1%; Average loss: 4.6056
Iteration: 45; Percent complete: 1.1%; Average loss: 4.5309
Iteration: 46; Percent complete: 1.1%; Average loss: 4.7480
Iteration: 47; Percent complete: 1.2%; Average loss: 4.6818
Iteration: 48; Percent complete: 1.2%; Average loss: 4.5164
Iteration: 49; Percent complete: 1.2%; Average loss: 4.4678
Iteration: 50; Percent complete: 1.2%; Average loss: 4.5997
Iteration: 51; Percent complete: 1.3%; Average loss: 4.5455
Iteration: 52; Percent complete: 1.3%; Average loss: 4.6628
Iteration: 53; Percent complete: 1.3%; Average loss: 4.5016
Iteration: 54; Percent complete: 1.4%; Average loss: 4.6610
Iteration: 55; Percent complete: 1.4%; Average loss: 4.6290
Iteration: 56; Percent complete: 1.4%; Average loss: 4.6434
Iteration: 57; Percent complete: 1.4%; Average loss: 4.4881
Iteration: 58; Percent complete: 1.5%; Average loss: 4.6454
Iteration: 59; Percent complete: 1.5%; Average loss: 4.5637
Iteration: 60; Percent complete: 1.5%; Average loss: 4.5736
Iteration: 61; Percent complete: 1.5%; Average loss: 4.6077
Iteration: 62; Percent complete: 1.6%; Average loss: 4.6325
Iteration: 63; Percent complete: 1.6%; Average loss: 4.5852
Iteration: 64; Percent complete: 1.6%; Average loss: 4.4723
Iteration: 65; Percent complete: 1.6%; Average loss: 4.6149
Iteration: 66; Percent complete: 1.7%; Average loss: 4.5447
Iteration: 67; Percent complete: 1.7%; Average loss: 4.6359
Iteration: 68; Percent complete: 1.7%; Average loss: 4.5270
Iteration: 69; Percent complete: 1.7%; Average loss: 4.5458
Iteration: 70; Percent complete: 1.8%; Average loss: 4.5235
Iteration: 71; Percent complete: 1.8%; Average loss: 4.4262
Iteration: 72; Percent complete: 1.8%; Average loss: 4.2718
Iteration: 73; Percent complete: 1.8%; Average loss: 4.8049
Iteration: 74; Percent complete: 1.8%; Average loss: 4.7331
Iteration: 75; Percent complete: 1.9%; Average loss: 4.5070
Iteration: 76; Percent complete: 1.9%; Average loss: 4.4455
Iteration: 77; Percent complete: 1.9%; Average loss: 4.1789
Iteration: 78; Percent complete: 1.9%; Average loss: 4.6710
Iteration: 79; Percent complete: 2.0%; Average loss: 4.5628
Iteration: 80; Percent complete: 2.0%; Average loss: 4.6154
Iteration: 81; Percent complete: 2.0%; Average loss: 4.3903
Iteration: 82; Percent complete: 2.1%; Average loss: 4.5381
Iteration: 83; Percent complete: 2.1%; Average loss: 4.3756
Iteration: 84; Percent complete: 2.1%; Average loss: 4.3986
Iteration: 85; Percent complete: 2.1%; Average loss: 4.7114
Iteration: 86; Percent complete: 2.1%; Average loss: 4.5023
Iteration: 87; Percent complete: 2.2%; Average loss: 4.2396
Iteration: 88; Percent complete: 2.2%; Average loss: 4.2797
Iteration: 89; Percent complete: 2.2%; Average loss: 4.6211
Iteration: 90; Percent complete: 2.2%; Average loss: 4.4979
Iteration: 91; Percent complete: 2.3%; Average loss: 4.5713
Iteration: 92; Percent complete: 2.3%; Average loss: 4.3451
Iteration: 93; Percent complete: 2.3%; Average loss: 4.4739
Iteration: 94; Percent complete: 2.4%; Average loss: 4.1861
Iteration: 95; Percent complete: 2.4%; Average loss: 4.6169
Iteration: 96; Percent complete: 2.4%; Average loss: 4.5712
Iteration: 97; Percent complete: 2.4%; Average loss: 4.5008
Iteration: 98; Percent complete: 2.5%; Average loss: 4.5151
Iteration: 99; Percent complete: 2.5%; Average loss: 4.4675
Iteration: 100; Percent complete: 2.5%; Average loss: 4.7275
Iteration: 101; Percent complete: 2.5%; Average loss: 4.5861
Iteration: 102; Percent complete: 2.5%; Average loss: 4.3352
Iteration: 103; Percent complete: 2.6%; Average loss: 4.3407
Iteration: 104; Percent complete: 2.6%; Average loss: 4.3641
Iteration: 105; Percent complete: 2.6%; Average loss: 4.4334
Iteration: 106; Percent complete: 2.6%; Average loss: 4.7927
Iteration: 107; Percent complete: 2.7%; Average loss: 4.3334
Iteration: 108; Percent complete: 2.7%; Average loss: 4.2531
Iteration: 109; Percent complete: 2.7%; Average loss: 4.1823
Iteration: 110; Percent complete: 2.8%; Average loss: 4.2145
Iteration: 111; Percent complete: 2.8%; Average loss: 4.1761
Iteration: 112; Percent complete: 2.8%; Average loss: 4.5077
Iteration: 113; Percent complete: 2.8%; Average loss: 4.4208
Iteration: 114; Percent complete: 2.9%; Average loss: 4.3439
Iteration: 115; Percent complete: 2.9%; Average loss: 4.4074
Iteration: 116; Percent complete: 2.9%; Average loss: 4.3249
Iteration: 117; Percent complete: 2.9%; Average loss: 4.3358
Iteration: 118; Percent complete: 2.9%; Average loss: 4.3013
Iteration: 119; Percent complete: 3.0%; Average loss: 4.2458
Iteration: 120; Percent complete: 3.0%; Average loss: 4.2493
Iteration: 121; Percent complete: 3.0%; Average loss: 4.0456
Iteration: 122; Percent complete: 3.0%; Average loss: 4.3982
Iteration: 123; Percent complete: 3.1%; Average loss: 4.2021
Iteration: 124; Percent complete: 3.1%; Average loss: 4.2839
Iteration: 125; Percent complete: 3.1%; Average loss: 4.4655
Iteration: 126; Percent complete: 3.1%; Average loss: 4.4940
Iteration: 127; Percent complete: 3.2%; Average loss: 4.5365
Iteration: 128; Percent complete: 3.2%; Average loss: 4.0220
Iteration: 129; Percent complete: 3.2%; Average loss: 4.3403
Iteration: 130; Percent complete: 3.2%; Average loss: 4.3818
Iteration: 131; Percent complete: 3.3%; Average loss: 4.2952
Iteration: 132; Percent complete: 3.3%; Average loss: 4.2097
Iteration: 133; Percent complete: 3.3%; Average loss: 4.4720
Iteration: 134; Percent complete: 3.4%; Average loss: 4.2915
Iteration: 135; Percent complete: 3.4%; Average loss: 4.2847
Iteration: 136; Percent complete: 3.4%; Average loss: 4.1892
Iteration: 137; Percent complete: 3.4%; Average loss: 4.3355
Iteration: 138; Percent complete: 3.5%; Average loss: 4.2452
Iteration: 139; Percent complete: 3.5%; Average loss: 4.2151
Iteration: 140; Percent complete: 3.5%; Average loss: 4.3712
Iteration: 141; Percent complete: 3.5%; Average loss: 4.1962
Iteration: 142; Percent complete: 3.5%; Average loss: 4.2893
Iteration: 143; Percent complete: 3.6%; Average loss: 4.1732
Iteration: 144; Percent complete: 3.6%; Average loss: 4.1443
Iteration: 145; Percent complete: 3.6%; Average loss: 4.3104
Iteration: 146; Percent complete: 3.6%; Average loss: 4.2731
Iteration: 147; Percent complete: 3.7%; Average loss: 4.2911
Iteration: 148; Percent complete: 3.7%; Average loss: 4.1268
Iteration: 149; Percent complete: 3.7%; Average loss: 4.2799
Iteration: 150; Percent complete: 3.8%; Average loss: 4.3238
Iteration: 151; Percent complete: 3.8%; Average loss: 4.1766
Iteration: 152; Percent complete: 3.8%; Average loss: 4.1340
Iteration: 153; Percent complete: 3.8%; Average loss: 4.2345
Iteration: 154; Percent complete: 3.9%; Average loss: 4.3790
Iteration: 155; Percent complete: 3.9%; Average loss: 4.4086
Iteration: 156; Percent complete: 3.9%; Average loss: 4.2170
Iteration: 157; Percent complete: 3.9%; Average loss: 4.3116
Iteration: 158; Percent complete: 4.0%; Average loss: 4.0699
Iteration: 159; Percent complete: 4.0%; Average loss: 4.1679
Iteration: 160; Percent complete: 4.0%; Average loss: 4.1141
Iteration: 161; Percent complete: 4.0%; Average loss: 4.1640
Iteration: 162; Percent complete: 4.0%; Average loss: 4.3242
Iteration: 163; Percent complete: 4.1%; Average loss: 4.1530
Iteration: 164; Percent complete: 4.1%; Average loss: 4.0813
Iteration: 165; Percent complete: 4.1%; Average loss: 4.0387
Iteration: 166; Percent complete: 4.2%; Average loss: 4.2814
Iteration: 167; Percent complete: 4.2%; Average loss: 4.1128
Iteration: 168; Percent complete: 4.2%; Average loss: 4.0239
Iteration: 169; Percent complete: 4.2%; Average loss: 4.2592
Iteration: 170; Percent complete: 4.2%; Average loss: 4.1787
Iteration: 171; Percent complete: 4.3%; Average loss: 4.0938
Iteration: 172; Percent complete: 4.3%; Average loss: 4.0352
Iteration: 173; Percent complete: 4.3%; Average loss: 3.9129
Iteration: 174; Percent complete: 4.3%; Average loss: 4.1943
Iteration: 175; Percent complete: 4.4%; Average loss: 4.3579
Iteration: 176; Percent complete: 4.4%; Average loss: 4.2054
Iteration: 177; Percent complete: 4.4%; Average loss: 4.2411
Iteration: 178; Percent complete: 4.5%; Average loss: 3.9769
Iteration: 179; Percent complete: 4.5%; Average loss: 4.1529
Iteration: 180; Percent complete: 4.5%; Average loss: 3.9527
Iteration: 181; Percent complete: 4.5%; Average loss: 4.1786
Iteration: 182; Percent complete: 4.5%; Average loss: 4.0194
Iteration: 183; Percent complete: 4.6%; Average loss: 3.9490
Iteration: 184; Percent complete: 4.6%; Average loss: 4.0119
Iteration: 185; Percent complete: 4.6%; Average loss: 4.2508
Iteration: 186; Percent complete: 4.7%; Average loss: 4.2307
Iteration: 187; Percent complete: 4.7%; Average loss: 3.8494
Iteration: 188; Percent complete: 4.7%; Average loss: 3.9176
Iteration: 189; Percent complete: 4.7%; Average loss: 4.1514
Iteration: 190; Percent complete: 4.8%; Average loss: 4.4015
Iteration: 191; Percent complete: 4.8%; Average loss: 3.9513
Iteration: 192; Percent complete: 4.8%; Average loss: 4.3636
Iteration: 193; Percent complete: 4.8%; Average loss: 4.1692
Iteration: 194; Percent complete: 4.9%; Average loss: 3.8491
Iteration: 195; Percent complete: 4.9%; Average loss: 4.1688
Iteration: 196; Percent complete: 4.9%; Average loss: 4.0475
Iteration: 197; Percent complete: 4.9%; Average loss: 4.0152
Iteration: 198; Percent complete: 5.0%; Average loss: 4.0539
Iteration: 199; Percent complete: 5.0%; Average loss: 4.1379
Iteration: 200; Percent complete: 5.0%; Average loss: 4.0600
Iteration: 201; Percent complete: 5.0%; Average loss: 3.8641
Iteration: 202; Percent complete: 5.1%; Average loss: 3.9400
Iteration: 203; Percent complete: 5.1%; Average loss: 3.9068
Iteration: 204; Percent complete: 5.1%; Average loss: 4.1728
Iteration: 205; Percent complete: 5.1%; Average loss: 4.0358
Iteration: 206; Percent complete: 5.1%; Average loss: 3.9809
Iteration: 207; Percent complete: 5.2%; Average loss: 4.1708
Iteration: 208; Percent complete: 5.2%; Average loss: 4.0098
Iteration: 209; Percent complete: 5.2%; Average loss: 3.9742
Iteration: 210; Percent complete: 5.2%; Average loss: 4.1831
Iteration: 211; Percent complete: 5.3%; Average loss: 4.1110
Iteration: 212; Percent complete: 5.3%; Average loss: 4.2007
Iteration: 213; Percent complete: 5.3%; Average loss: 4.1171
Iteration: 214; Percent complete: 5.3%; Average loss: 4.2443
Iteration: 215; Percent complete: 5.4%; Average loss: 4.0094
Iteration: 216; Percent complete: 5.4%; Average loss: 4.2510
Iteration: 217; Percent complete: 5.4%; Average loss: 4.2139
Iteration: 218; Percent complete: 5.5%; Average loss: 3.8531
Iteration: 219; Percent complete: 5.5%; Average loss: 3.9280
Iteration: 220; Percent complete: 5.5%; Average loss: 3.8787
Iteration: 221; Percent complete: 5.5%; Average loss: 4.0333
Iteration: 222; Percent complete: 5.5%; Average loss: 4.1290
Iteration: 223; Percent complete: 5.6%; Average loss: 4.0145
Iteration: 224; Percent complete: 5.6%; Average loss: 3.7487
Iteration: 225; Percent complete: 5.6%; Average loss: 4.1603
Iteration: 226; Percent complete: 5.7%; Average loss: 4.1985
Iteration: 227; Percent complete: 5.7%; Average loss: 4.1921
Iteration: 228; Percent complete: 5.7%; Average loss: 4.0379
Iteration: 229; Percent complete: 5.7%; Average loss: 3.9465
Iteration: 230; Percent complete: 5.8%; Average loss: 4.0422
Iteration: 231; Percent complete: 5.8%; Average loss: 3.9321
Iteration: 232; Percent complete: 5.8%; Average loss: 4.1777
Iteration: 233; Percent complete: 5.8%; Average loss: 4.0983
Iteration: 234; Percent complete: 5.9%; Average loss: 3.8849
Iteration: 235; Percent complete: 5.9%; Average loss: 3.8515
Iteration: 236; Percent complete: 5.9%; Average loss: 3.9281
Iteration: 237; Percent complete: 5.9%; Average loss: 3.9462
Iteration: 238; Percent complete: 5.9%; Average loss: 4.1049
Iteration: 239; Percent complete: 6.0%; Average loss: 3.7980
Iteration: 240; Percent complete: 6.0%; Average loss: 4.0713
Iteration: 241; Percent complete: 6.0%; Average loss: 4.3233
Iteration: 242; Percent complete: 6.0%; Average loss: 3.8460
Iteration: 243; Percent complete: 6.1%; Average loss: 4.2039
Iteration: 244; Percent complete: 6.1%; Average loss: 4.0009
Iteration: 245; Percent complete: 6.1%; Average loss: 3.9118
Iteration: 246; Percent complete: 6.2%; Average loss: 4.1729
Iteration: 247; Percent complete: 6.2%; Average loss: 4.1383
Iteration: 248; Percent complete: 6.2%; Average loss: 3.9499
Iteration: 249; Percent complete: 6.2%; Average loss: 3.7718
Iteration: 250; Percent complete: 6.2%; Average loss: 4.0863
Iteration: 251; Percent complete: 6.3%; Average loss: 4.1399
Iteration: 252; Percent complete: 6.3%; Average loss: 3.7995
Iteration: 253; Percent complete: 6.3%; Average loss: 3.7499
Iteration: 254; Percent complete: 6.3%; Average loss: 3.8995
Iteration: 255; Percent complete: 6.4%; Average loss: 3.8467
Iteration: 256; Percent complete: 6.4%; Average loss: 4.0602
Iteration: 257; Percent complete: 6.4%; Average loss: 4.0071
Iteration: 258; Percent complete: 6.5%; Average loss: 3.9945
Iteration: 259; Percent complete: 6.5%; Average loss: 3.8202
Iteration: 260; Percent complete: 6.5%; Average loss: 4.1252
Iteration: 261; Percent complete: 6.5%; Average loss: 3.8175
Iteration: 262; Percent complete: 6.6%; Average loss: 4.0881
Iteration: 263; Percent complete: 6.6%; Average loss: 4.0113
Iteration: 264; Percent complete: 6.6%; Average loss: 4.0317
Iteration: 265; Percent complete: 6.6%; Average loss: 3.9326
Iteration: 266; Percent complete: 6.7%; Average loss: 3.8277
Iteration: 267; Percent complete: 6.7%; Average loss: 3.9498
Iteration: 268; Percent complete: 6.7%; Average loss: 4.0803
Iteration: 269; Percent complete: 6.7%; Average loss: 3.9833
Iteration: 270; Percent complete: 6.8%; Average loss: 3.8172
Iteration: 271; Percent complete: 6.8%; Average loss: 3.7643
Iteration: 272; Percent complete: 6.8%; Average loss: 4.0420
Iteration: 273; Percent complete: 6.8%; Average loss: 3.9423
Iteration: 274; Percent complete: 6.9%; Average loss: 3.9199
Iteration: 275; Percent complete: 6.9%; Average loss: 4.3177
Iteration: 276; Percent complete: 6.9%; Average loss: 3.7478
Iteration: 277; Percent complete: 6.9%; Average loss: 3.7620
Iteration: 278; Percent complete: 7.0%; Average loss: 3.7885
Iteration: 279; Percent complete: 7.0%; Average loss: 3.8156
Iteration: 280; Percent complete: 7.0%; Average loss: 3.9616
Iteration: 281; Percent complete: 7.0%; Average loss: 3.8404
Iteration: 282; Percent complete: 7.0%; Average loss: 3.8787
Iteration: 283; Percent complete: 7.1%; Average loss: 3.9835
Iteration: 284; Percent complete: 7.1%; Average loss: 3.9675
Iteration: 285; Percent complete: 7.1%; Average loss: 4.1017
Iteration: 286; Percent complete: 7.1%; Average loss: 4.1266
Iteration: 287; Percent complete: 7.2%; Average loss: 3.8675
Iteration: 288; Percent complete: 7.2%; Average loss: 3.8331
Iteration: 289; Percent complete: 7.2%; Average loss: 3.9470
Iteration: 290; Percent complete: 7.2%; Average loss: 4.1863
Iteration: 291; Percent complete: 7.3%; Average loss: 4.1021
Iteration: 292; Percent complete: 7.3%; Average loss: 3.8626
Iteration: 293; Percent complete: 7.3%; Average loss: 3.9560
Iteration: 294; Percent complete: 7.3%; Average loss: 3.9117
Iteration: 295; Percent complete: 7.4%; Average loss: 4.1402
Iteration: 296; Percent complete: 7.4%; Average loss: 4.0499
Iteration: 297; Percent complete: 7.4%; Average loss: 3.7742
Iteration: 298; Percent complete: 7.4%; Average loss: 3.9359
Iteration: 299; Percent complete: 7.5%; Average loss: 3.9271
Iteration: 300; Percent complete: 7.5%; Average loss: 3.8686
Iteration: 301; Percent complete: 7.5%; Average loss: 3.9966
Iteration: 302; Percent complete: 7.5%; Average loss: 3.9275
Iteration: 303; Percent complete: 7.6%; Average loss: 4.2573
Iteration: 304; Percent complete: 7.6%; Average loss: 3.8739
Iteration: 305; Percent complete: 7.6%; Average loss: 3.9361
Iteration: 306; Percent complete: 7.6%; Average loss: 3.9089
Iteration: 307; Percent complete: 7.7%; Average loss: 4.2990
Iteration: 308; Percent complete: 7.7%; Average loss: 3.9199
Iteration: 309; Percent complete: 7.7%; Average loss: 3.8696
Iteration: 310; Percent complete: 7.8%; Average loss: 3.8743
Iteration: 311; Percent complete: 7.8%; Average loss: 4.0957
Iteration: 312; Percent complete: 7.8%; Average loss: 3.6966
Iteration: 313; Percent complete: 7.8%; Average loss: 4.0215
Iteration: 314; Percent complete: 7.8%; Average loss: 3.9167
Iteration: 315; Percent complete: 7.9%; Average loss: 3.8345
Iteration: 316; Percent complete: 7.9%; Average loss: 3.6035
Iteration: 317; Percent complete: 7.9%; Average loss: 3.7024
Iteration: 318; Percent complete: 8.0%; Average loss: 3.7437
Iteration: 319; Percent complete: 8.0%; Average loss: 3.9756
Iteration: 320; Percent complete: 8.0%; Average loss: 3.8505
Iteration: 321; Percent complete: 8.0%; Average loss: 3.7763
Iteration: 322; Percent complete: 8.1%; Average loss: 3.9118
Iteration: 323; Percent complete: 8.1%; Average loss: 3.7364
Iteration: 324; Percent complete: 8.1%; Average loss: 3.7454
Iteration: 325; Percent complete: 8.1%; Average loss: 3.9057
Iteration: 326; Percent complete: 8.2%; Average loss: 3.9075
Iteration: 327; Percent complete: 8.2%; Average loss: 3.7333
Iteration: 328; Percent complete: 8.2%; Average loss: 3.6959
Iteration: 329; Percent complete: 8.2%; Average loss: 4.1077
Iteration: 330; Percent complete: 8.2%; Average loss: 3.7091
Iteration: 331; Percent complete: 8.3%; Average loss: 3.6840
Iteration: 332; Percent complete: 8.3%; Average loss: 4.1962
Iteration: 333; Percent complete: 8.3%; Average loss: 3.9732
Iteration: 334; Percent complete: 8.3%; Average loss: 3.9365
Iteration: 335; Percent complete: 8.4%; Average loss: 3.9541
Iteration: 336; Percent complete: 8.4%; Average loss: 3.7173
Iteration: 337; Percent complete: 8.4%; Average loss: 3.9089
Iteration: 338; Percent complete: 8.5%; Average loss: 3.9108
Iteration: 339; Percent complete: 8.5%; Average loss: 4.0485
Iteration: 340; Percent complete: 8.5%; Average loss: 3.6254
Iteration: 341; Percent complete: 8.5%; Average loss: 3.7100
Iteration: 342; Percent complete: 8.6%; Average loss: 3.6576
Iteration: 343; Percent complete: 8.6%; Average loss: 3.8029
Iteration: 344; Percent complete: 8.6%; Average loss: 3.7342
Iteration: 345; Percent complete: 8.6%; Average loss: 3.7626
Iteration: 346; Percent complete: 8.6%; Average loss: 3.5534
Iteration: 347; Percent complete: 8.7%; Average loss: 3.8376
Iteration: 348; Percent complete: 8.7%; Average loss: 3.7843
Iteration: 349; Percent complete: 8.7%; Average loss: 3.8787
Iteration: 350; Percent complete: 8.8%; Average loss: 3.9097
Iteration: 351; Percent complete: 8.8%; Average loss: 3.8091
Iteration: 352; Percent complete: 8.8%; Average loss: 3.6724
Iteration: 353; Percent complete: 8.8%; Average loss: 3.8542
Iteration: 354; Percent complete: 8.8%; Average loss: 4.1248
Iteration: 355; Percent complete: 8.9%; Average loss: 3.7263
Iteration: 356; Percent complete: 8.9%; Average loss: 4.0245
Iteration: 357; Percent complete: 8.9%; Average loss: 3.9130
Iteration: 358; Percent complete: 8.9%; Average loss: 3.9195
Iteration: 359; Percent complete: 9.0%; Average loss: 3.8992
Iteration: 360; Percent complete: 9.0%; Average loss: 3.8383
Iteration: 361; Percent complete: 9.0%; Average loss: 3.7975
Iteration: 362; Percent complete: 9.0%; Average loss: 3.7973
Iteration: 363; Percent complete: 9.1%; Average loss: 3.8448
Iteration: 364; Percent complete: 9.1%; Average loss: 3.9384
Iteration: 365; Percent complete: 9.1%; Average loss: 3.8512
Iteration: 366; Percent complete: 9.2%; Average loss: 3.7244
Iteration: 367; Percent complete: 9.2%; Average loss: 4.0117
Iteration: 368; Percent complete: 9.2%; Average loss: 3.7462
Iteration: 369; Percent complete: 9.2%; Average loss: 3.7958
Iteration: 370; Percent complete: 9.2%; Average loss: 3.5562
Iteration: 371; Percent complete: 9.3%; Average loss: 3.8421
Iteration: 372; Percent complete: 9.3%; Average loss: 3.9372
Iteration: 373; Percent complete: 9.3%; Average loss: 3.6849
Iteration: 374; Percent complete: 9.3%; Average loss: 4.0690
Iteration: 375; Percent complete: 9.4%; Average loss: 3.6387
Iteration: 376; Percent complete: 9.4%; Average loss: 4.0816
Iteration: 377; Percent complete: 9.4%; Average loss: 3.6204
Iteration: 378; Percent complete: 9.4%; Average loss: 3.9052
Iteration: 379; Percent complete: 9.5%; Average loss: 3.7347
Iteration: 380; Percent complete: 9.5%; Average loss: 3.8060
Iteration: 381; Percent complete: 9.5%; Average loss: 3.6983
Iteration: 382; Percent complete: 9.6%; Average loss: 3.9398
Iteration: 383; Percent complete: 9.6%; Average loss: 3.7305
Iteration: 384; Percent complete: 9.6%; Average loss: 3.7554
Iteration: 385; Percent complete: 9.6%; Average loss: 3.9453
Iteration: 386; Percent complete: 9.7%; Average loss: 3.8717
Iteration: 387; Percent complete: 9.7%; Average loss: 3.9855
Iteration: 388; Percent complete: 9.7%; Average loss: 3.7109
Iteration: 389; Percent complete: 9.7%; Average loss: 3.7190
Iteration: 390; Percent complete: 9.8%; Average loss: 4.1139
Iteration: 391; Percent complete: 9.8%; Average loss: 3.7700
Iteration: 392; Percent complete: 9.8%; Average loss: 3.7483
Iteration: 393; Percent complete: 9.8%; Average loss: 3.7968
Iteration: 394; Percent complete: 9.8%; Average loss: 3.9053
Iteration: 395; Percent complete: 9.9%; Average loss: 3.8599
Iteration: 396; Percent complete: 9.9%; Average loss: 3.4934
Iteration: 397; Percent complete: 9.9%; Average loss: 3.6663
Iteration: 398; Percent complete: 10.0%; Average loss: 3.8706
Iteration: 399; Percent complete: 10.0%; Average loss: 3.8983
Iteration: 400; Percent complete: 10.0%; Average loss: 3.8912
Iteration: 401; Percent complete: 10.0%; Average loss: 3.6591
Iteration: 402; Percent complete: 10.1%; Average loss: 3.9495
Iteration: 403; Percent complete: 10.1%; Average loss: 3.7703
Iteration: 404; Percent complete: 10.1%; Average loss: 3.8298
Iteration: 405; Percent complete: 10.1%; Average loss: 3.8102
Iteration: 406; Percent complete: 10.2%; Average loss: 3.8853
Iteration: 407; Percent complete: 10.2%; Average loss: 3.6067
Iteration: 408; Percent complete: 10.2%; Average loss: 3.7128
Iteration: 409; Percent complete: 10.2%; Average loss: 3.9816
Iteration: 410; Percent complete: 10.2%; Average loss: 3.8357
Iteration: 411; Percent complete: 10.3%; Average loss: 3.5076
Iteration: 412; Percent complete: 10.3%; Average loss: 3.8769
Iteration: 413; Percent complete: 10.3%; Average loss: 3.8182
Iteration: 414; Percent complete: 10.3%; Average loss: 3.7555
Iteration: 415; Percent complete: 10.4%; Average loss: 3.6896
Iteration: 416; Percent complete: 10.4%; Average loss: 3.9664
Iteration: 417; Percent complete: 10.4%; Average loss: 4.0601
Iteration: 418; Percent complete: 10.4%; Average loss: 3.8940
Iteration: 419; Percent complete: 10.5%; Average loss: 3.7524
Iteration: 420; Percent complete: 10.5%; Average loss: 3.6331
Iteration: 421; Percent complete: 10.5%; Average loss: 3.5097
Iteration: 422; Percent complete: 10.5%; Average loss: 3.6812
Iteration: 423; Percent complete: 10.6%; Average loss: 3.8914
Iteration: 424; Percent complete: 10.6%; Average loss: 3.8814
Iteration: 425; Percent complete: 10.6%; Average loss: 3.7475
Iteration: 426; Percent complete: 10.7%; Average loss: 3.9066
Iteration: 427; Percent complete: 10.7%; Average loss: 3.5569
Iteration: 428; Percent complete: 10.7%; Average loss: 3.8284
Iteration: 429; Percent complete: 10.7%; Average loss: 3.7919
Iteration: 430; Percent complete: 10.8%; Average loss: 3.8281
Iteration: 431; Percent complete: 10.8%; Average loss: 3.7995
Iteration: 432; Percent complete: 10.8%; Average loss: 3.8025
Iteration: 433; Percent complete: 10.8%; Average loss: 3.8430
Iteration: 434; Percent complete: 10.8%; Average loss: 3.4809
Iteration: 435; Percent complete: 10.9%; Average loss: 3.8218
Iteration: 436; Percent complete: 10.9%; Average loss: 3.7494
Iteration: 437; Percent complete: 10.9%; Average loss: 3.8251
Iteration: 438; Percent complete: 10.9%; Average loss: 3.9423
Iteration: 439; Percent complete: 11.0%; Average loss: 3.9103
Iteration: 440; Percent complete: 11.0%; Average loss: 3.5101
Iteration: 441; Percent complete: 11.0%; Average loss: 3.7384
Iteration: 442; Percent complete: 11.1%; Average loss: 3.9870
Iteration: 443; Percent complete: 11.1%; Average loss: 3.7450
Iteration: 444; Percent complete: 11.1%; Average loss: 3.6294
Iteration: 445; Percent complete: 11.1%; Average loss: 3.8222
Iteration: 446; Percent complete: 11.2%; Average loss: 3.8110
Iteration: 447; Percent complete: 11.2%; Average loss: 3.8280
Iteration: 448; Percent complete: 11.2%; Average loss: 3.6043
Iteration: 449; Percent complete: 11.2%; Average loss: 3.8028
Iteration: 450; Percent complete: 11.2%; Average loss: 3.5299
Iteration: 451; Percent complete: 11.3%; Average loss: 3.5892
Iteration: 452; Percent complete: 11.3%; Average loss: 3.8365
Iteration: 453; Percent complete: 11.3%; Average loss: 3.9424
Iteration: 454; Percent complete: 11.3%; Average loss: 3.7069
Iteration: 455; Percent complete: 11.4%; Average loss: 3.9661
Iteration: 456; Percent complete: 11.4%; Average loss: 3.8078
Iteration: 457; Percent complete: 11.4%; Average loss: 4.2279
Iteration: 458; Percent complete: 11.5%; Average loss: 3.8765
Iteration: 459; Percent complete: 11.5%; Average loss: 3.6795
Iteration: 460; Percent complete: 11.5%; Average loss: 3.5282
Iteration: 461; Percent complete: 11.5%; Average loss: 3.4925
Iteration: 462; Percent complete: 11.6%; Average loss: 3.8257
Iteration: 463; Percent complete: 11.6%; Average loss: 3.7596
Iteration: 464; Percent complete: 11.6%; Average loss: 3.9736
Iteration: 465; Percent complete: 11.6%; Average loss: 3.5580
Iteration: 466; Percent complete: 11.7%; Average loss: 3.7508
Iteration: 467; Percent complete: 11.7%; Average loss: 3.7318
Iteration: 468; Percent complete: 11.7%; Average loss: 3.5071
Iteration: 469; Percent complete: 11.7%; Average loss: 3.6243
Iteration: 470; Percent complete: 11.8%; Average loss: 4.1323
Iteration: 471; Percent complete: 11.8%; Average loss: 3.9348
Iteration: 472; Percent complete: 11.8%; Average loss: 3.8424
Iteration: 473; Percent complete: 11.8%; Average loss: 3.6874
Iteration: 474; Percent complete: 11.8%; Average loss: 3.7322
Iteration: 475; Percent complete: 11.9%; Average loss: 3.6266
Iteration: 476; Percent complete: 11.9%; Average loss: 3.6212
Iteration: 477; Percent complete: 11.9%; Average loss: 3.6878
Iteration: 478; Percent complete: 11.9%; Average loss: 4.0651
Iteration: 479; Percent complete: 12.0%; Average loss: 3.8638
Iteration: 480; Percent complete: 12.0%; Average loss: 4.0088
Iteration: 481; Percent complete: 12.0%; Average loss: 3.6000
Iteration: 482; Percent complete: 12.0%; Average loss: 3.7364
Iteration: 483; Percent complete: 12.1%; Average loss: 3.6628
Iteration: 484; Percent complete: 12.1%; Average loss: 3.8373
Iteration: 485; Percent complete: 12.1%; Average loss: 3.8257
Iteration: 486; Percent complete: 12.2%; Average loss: 3.7358
Iteration: 487; Percent complete: 12.2%; Average loss: 3.7522
Iteration: 488; Percent complete: 12.2%; Average loss: 3.6053
Iteration: 489; Percent complete: 12.2%; Average loss: 3.7155
Iteration: 490; Percent complete: 12.2%; Average loss: 3.4817
Iteration: 491; Percent complete: 12.3%; Average loss: 3.4262
Iteration: 492; Percent complete: 12.3%; Average loss: 3.9253
Iteration: 493; Percent complete: 12.3%; Average loss: 3.8757
Iteration: 494; Percent complete: 12.3%; Average loss: 3.9800
Iteration: 495; Percent complete: 12.4%; Average loss: 3.6920
Iteration: 496; Percent complete: 12.4%; Average loss: 3.6780
Iteration: 497; Percent complete: 12.4%; Average loss: 3.7345
Iteration: 498; Percent complete: 12.4%; Average loss: 3.6125
Iteration: 499; Percent complete: 12.5%; Average loss: 3.6583
Iteration: 500; Percent complete: 12.5%; Average loss: 3.6704
Iteration: 501; Percent complete: 12.5%; Average loss: 3.6934
Iteration: 502; Percent complete: 12.6%; Average loss: 3.7784
Iteration: 503; Percent complete: 12.6%; Average loss: 3.7291
Iteration: 504; Percent complete: 12.6%; Average loss: 3.7097
Iteration: 505; Percent complete: 12.6%; Average loss: 3.6182
Iteration: 506; Percent complete: 12.7%; Average loss: 3.7857
Iteration: 507; Percent complete: 12.7%; Average loss: 3.4794
Iteration: 508; Percent complete: 12.7%; Average loss: 3.8963
Iteration: 509; Percent complete: 12.7%; Average loss: 3.6132
Iteration: 510; Percent complete: 12.8%; Average loss: 3.7421
Iteration: 511; Percent complete: 12.8%; Average loss: 3.6630
Iteration: 512; Percent complete: 12.8%; Average loss: 3.6766
Iteration: 513; Percent complete: 12.8%; Average loss: 3.5670
Iteration: 514; Percent complete: 12.8%; Average loss: 3.9844
Iteration: 515; Percent complete: 12.9%; Average loss: 3.7784
Iteration: 516; Percent complete: 12.9%; Average loss: 3.6683
Iteration: 517; Percent complete: 12.9%; Average loss: 4.0683
Iteration: 518; Percent complete: 13.0%; Average loss: 3.7425
Iteration: 519; Percent complete: 13.0%; Average loss: 3.8126
Iteration: 520; Percent complete: 13.0%; Average loss: 3.7731
Iteration: 521; Percent complete: 13.0%; Average loss: 3.7856
Iteration: 522; Percent complete: 13.1%; Average loss: 3.7573
Iteration: 523; Percent complete: 13.1%; Average loss: 3.4520
Iteration: 524; Percent complete: 13.1%; Average loss: 3.7545
Iteration: 525; Percent complete: 13.1%; Average loss: 3.7903
Iteration: 526; Percent complete: 13.2%; Average loss: 3.4897
Iteration: 527; Percent complete: 13.2%; Average loss: 3.7155
Iteration: 528; Percent complete: 13.2%; Average loss: 3.7966
Iteration: 529; Percent complete: 13.2%; Average loss: 3.5634
Iteration: 530; Percent complete: 13.2%; Average loss: 3.5543
Iteration: 531; Percent complete: 13.3%; Average loss: 3.6797
Iteration: 532; Percent complete: 13.3%; Average loss: 3.7293
Iteration: 533; Percent complete: 13.3%; Average loss: 3.6752
Iteration: 534; Percent complete: 13.4%; Average loss: 3.9895
Iteration: 535; Percent complete: 13.4%; Average loss: 3.4879
Iteration: 536; Percent complete: 13.4%; Average loss: 3.5960
Iteration: 537; Percent complete: 13.4%; Average loss: 3.7389
Iteration: 538; Percent complete: 13.5%; Average loss: 3.6945
Iteration: 539; Percent complete: 13.5%; Average loss: 3.7894
Iteration: 540; Percent complete: 13.5%; Average loss: 3.8123
Iteration: 541; Percent complete: 13.5%; Average loss: 3.7396
Iteration: 542; Percent complete: 13.6%; Average loss: 3.4326
Iteration: 543; Percent complete: 13.6%; Average loss: 3.7959
Iteration: 544; Percent complete: 13.6%; Average loss: 3.2991
Iteration: 545; Percent complete: 13.6%; Average loss: 3.8910
Iteration: 546; Percent complete: 13.7%; Average loss: 3.4528
Iteration: 547; Percent complete: 13.7%; Average loss: 3.6254
Iteration: 548; Percent complete: 13.7%; Average loss: 3.8538
Iteration: 549; Percent complete: 13.7%; Average loss: 3.6249
Iteration: 550; Percent complete: 13.8%; Average loss: 3.5090
Iteration: 551; Percent complete: 13.8%; Average loss: 3.7320
Iteration: 552; Percent complete: 13.8%; Average loss: 3.6639
Iteration: 553; Percent complete: 13.8%; Average loss: 3.9292
Iteration: 554; Percent complete: 13.9%; Average loss: 3.6778
Iteration: 555; Percent complete: 13.9%; Average loss: 3.4766
Iteration: 556; Percent complete: 13.9%; Average loss: 3.9454
Iteration: 557; Percent complete: 13.9%; Average loss: 3.5767
Iteration: 558; Percent complete: 14.0%; Average loss: 3.6528
Iteration: 559; Percent complete: 14.0%; Average loss: 3.6668
Iteration: 560; Percent complete: 14.0%; Average loss: 3.6750
Iteration: 561; Percent complete: 14.0%; Average loss: 3.8469
Iteration: 562; Percent complete: 14.1%; Average loss: 3.7510
Iteration: 563; Percent complete: 14.1%; Average loss: 3.4060
Iteration: 564; Percent complete: 14.1%; Average loss: 3.6670
Iteration: 565; Percent complete: 14.1%; Average loss: 3.5087
Iteration: 566; Percent complete: 14.1%; Average loss: 3.5488
Iteration: 567; Percent complete: 14.2%; Average loss: 3.4677
Iteration: 568; Percent complete: 14.2%; Average loss: 3.7264
Iteration: 569; Percent complete: 14.2%; Average loss: 3.6317
Iteration: 570; Percent complete: 14.2%; Average loss: 3.6415
Iteration: 571; Percent complete: 14.3%; Average loss: 3.5073
Iteration: 572; Percent complete: 14.3%; Average loss: 3.8177
Iteration: 573; Percent complete: 14.3%; Average loss: 3.6691
Iteration: 574; Percent complete: 14.3%; Average loss: 3.4024
Iteration: 575; Percent complete: 14.4%; Average loss: 3.4879
Iteration: 576; Percent complete: 14.4%; Average loss: 3.7828
Iteration: 577; Percent complete: 14.4%; Average loss: 3.5500
Iteration: 578; Percent complete: 14.4%; Average loss: 3.5785
Iteration: 579; Percent complete: 14.5%; Average loss: 3.7351
Iteration: 580; Percent complete: 14.5%; Average loss: 3.6855
Iteration: 581; Percent complete: 14.5%; Average loss: 3.8661
Iteration: 582; Percent complete: 14.5%; Average loss: 3.5707
Iteration: 583; Percent complete: 14.6%; Average loss: 3.6714
Iteration: 584; Percent complete: 14.6%; Average loss: 3.6304
Iteration: 585; Percent complete: 14.6%; Average loss: 3.7546
Iteration: 586; Percent complete: 14.6%; Average loss: 3.8906
Iteration: 587; Percent complete: 14.7%; Average loss: 3.7497
Iteration: 588; Percent complete: 14.7%; Average loss: 3.6837
Iteration: 589; Percent complete: 14.7%; Average loss: 3.9890
Iteration: 590; Percent complete: 14.8%; Average loss: 3.7218
Iteration: 591; Percent complete: 14.8%; Average loss: 3.5060
Iteration: 592; Percent complete: 14.8%; Average loss: 3.7367
Iteration: 593; Percent complete: 14.8%; Average loss: 3.5484
Iteration: 594; Percent complete: 14.8%; Average loss: 3.8208
Iteration: 595; Percent complete: 14.9%; Average loss: 3.5792
Iteration: 596; Percent complete: 14.9%; Average loss: 3.9039
Iteration: 597; Percent complete: 14.9%; Average loss: 3.5220
Iteration: 598; Percent complete: 14.9%; Average loss: 3.7021
Iteration: 599; Percent complete: 15.0%; Average loss: 3.6205
Iteration: 600; Percent complete: 15.0%; Average loss: 3.6438
Iteration: 601; Percent complete: 15.0%; Average loss: 3.7623
Iteration: 602; Percent complete: 15.0%; Average loss: 3.6062
Iteration: 603; Percent complete: 15.1%; Average loss: 3.6464
Iteration: 604; Percent complete: 15.1%; Average loss: 3.5077
Iteration: 605; Percent complete: 15.1%; Average loss: 3.4794
Iteration: 606; Percent complete: 15.2%; Average loss: 3.8511
Iteration: 607; Percent complete: 15.2%; Average loss: 3.6327
Iteration: 608; Percent complete: 15.2%; Average loss: 3.6706
Iteration: 609; Percent complete: 15.2%; Average loss: 3.4531
Iteration: 610; Percent complete: 15.2%; Average loss: 3.7988
Iteration: 611; Percent complete: 15.3%; Average loss: 3.8275
Iteration: 612; Percent complete: 15.3%; Average loss: 3.8428
Iteration: 613; Percent complete: 15.3%; Average loss: 3.7894
Iteration: 614; Percent complete: 15.3%; Average loss: 3.4149
Iteration: 615; Percent complete: 15.4%; Average loss: 4.0131
Iteration: 616; Percent complete: 15.4%; Average loss: 3.4889
Iteration: 617; Percent complete: 15.4%; Average loss: 3.8211
Iteration: 618; Percent complete: 15.4%; Average loss: 3.5879
Iteration: 619; Percent complete: 15.5%; Average loss: 3.6240
Iteration: 620; Percent complete: 15.5%; Average loss: 3.5489
Iteration: 621; Percent complete: 15.5%; Average loss: 3.7530
Iteration: 622; Percent complete: 15.6%; Average loss: 3.3821
Iteration: 623; Percent complete: 15.6%; Average loss: 3.8146
Iteration: 624; Percent complete: 15.6%; Average loss: 3.9380
Iteration: 625; Percent complete: 15.6%; Average loss: 3.4655
Iteration: 626; Percent complete: 15.7%; Average loss: 3.6114
Iteration: 627; Percent complete: 15.7%; Average loss: 3.6481
Iteration: 628; Percent complete: 15.7%; Average loss: 3.5326
Iteration: 629; Percent complete: 15.7%; Average loss: 3.3729
Iteration: 630; Percent complete: 15.8%; Average loss: 3.5756
Iteration: 631; Percent complete: 15.8%; Average loss: 3.9363
Iteration: 632; Percent complete: 15.8%; Average loss: 3.3567
Iteration: 633; Percent complete: 15.8%; Average loss: 3.7134
Iteration: 634; Percent complete: 15.8%; Average loss: 3.6170
Iteration: 635; Percent complete: 15.9%; Average loss: 3.6112
Iteration: 636; Percent complete: 15.9%; Average loss: 3.4521
Iteration: 637; Percent complete: 15.9%; Average loss: 3.7653
Iteration: 638; Percent complete: 16.0%; Average loss: 3.5805
Iteration: 639; Percent complete: 16.0%; Average loss: 3.6432
Iteration: 640; Percent complete: 16.0%; Average loss: 3.6718
Iteration: 641; Percent complete: 16.0%; Average loss: 3.7241
Iteration: 642; Percent complete: 16.1%; Average loss: 3.5902
Iteration: 643; Percent complete: 16.1%; Average loss: 3.6668
Iteration: 644; Percent complete: 16.1%; Average loss: 3.7633
Iteration: 645; Percent complete: 16.1%; Average loss: 3.5397
Iteration: 646; Percent complete: 16.2%; Average loss: 3.7546
Iteration: 647; Percent complete: 16.2%; Average loss: 3.5546
Iteration: 648; Percent complete: 16.2%; Average loss: 3.5635
Iteration: 649; Percent complete: 16.2%; Average loss: 3.6538
Iteration: 650; Percent complete: 16.2%; Average loss: 3.7647
Iteration: 651; Percent complete: 16.3%; Average loss: 3.5336
Iteration: 652; Percent complete: 16.3%; Average loss: 3.4311
Iteration: 653; Percent complete: 16.3%; Average loss: 3.6578
Iteration: 654; Percent complete: 16.4%; Average loss: 3.8485
Iteration: 655; Percent complete: 16.4%; Average loss: 3.5187
Iteration: 656; Percent complete: 16.4%; Average loss: 3.6335
Iteration: 657; Percent complete: 16.4%; Average loss: 3.7544
Iteration: 658; Percent complete: 16.4%; Average loss: 3.4882
Iteration: 659; Percent complete: 16.5%; Average loss: 3.2699
Iteration: 660; Percent complete: 16.5%; Average loss: 3.4721
Iteration: 661; Percent complete: 16.5%; Average loss: 3.6611
Iteration: 662; Percent complete: 16.6%; Average loss: 3.7456
Iteration: 663; Percent complete: 16.6%; Average loss: 3.5059
Iteration: 664; Percent complete: 16.6%; Average loss: 3.3795
Iteration: 665; Percent complete: 16.6%; Average loss: 3.6558
Iteration: 666; Percent complete: 16.7%; Average loss: 3.5529
Iteration: 667; Percent complete: 16.7%; Average loss: 3.5709
Iteration: 668; Percent complete: 16.7%; Average loss: 3.5261
Iteration: 669; Percent complete: 16.7%; Average loss: 3.4166
Iteration: 670; Percent complete: 16.8%; Average loss: 3.6772
Iteration: 671; Percent complete: 16.8%; Average loss: 3.5699
Iteration: 672; Percent complete: 16.8%; Average loss: 3.5724
Iteration: 673; Percent complete: 16.8%; Average loss: 3.6077
Iteration: 674; Percent complete: 16.9%; Average loss: 3.6795
Iteration: 675; Percent complete: 16.9%; Average loss: 3.7656
Iteration: 676; Percent complete: 16.9%; Average loss: 3.4894
Iteration: 677; Percent complete: 16.9%; Average loss: 3.6981
Iteration: 678; Percent complete: 17.0%; Average loss: 3.7619
Iteration: 679; Percent complete: 17.0%; Average loss: 3.5635
Iteration: 680; Percent complete: 17.0%; Average loss: 3.5198
Iteration: 681; Percent complete: 17.0%; Average loss: 3.9840
Iteration: 682; Percent complete: 17.1%; Average loss: 3.5048
Iteration: 683; Percent complete: 17.1%; Average loss: 3.6082
Iteration: 684; Percent complete: 17.1%; Average loss: 3.5738
Iteration: 685; Percent complete: 17.1%; Average loss: 3.5225
Iteration: 686; Percent complete: 17.2%; Average loss: 3.6038
Iteration: 687; Percent complete: 17.2%; Average loss: 3.7518
Iteration: 688; Percent complete: 17.2%; Average loss: 3.6029
Iteration: 689; Percent complete: 17.2%; Average loss: 3.6429
Iteration: 690; Percent complete: 17.2%; Average loss: 3.5277
Iteration: 691; Percent complete: 17.3%; Average loss: 3.8561
Iteration: 692; Percent complete: 17.3%; Average loss: 3.3160
Iteration: 693; Percent complete: 17.3%; Average loss: 3.6950
Iteration: 694; Percent complete: 17.3%; Average loss: 3.6165
Iteration: 695; Percent complete: 17.4%; Average loss: 3.2826
Iteration: 696; Percent complete: 17.4%; Average loss: 3.7780
Iteration: 697; Percent complete: 17.4%; Average loss: 3.8313
Iteration: 698; Percent complete: 17.4%; Average loss: 3.4934
Iteration: 699; Percent complete: 17.5%; Average loss: 3.7378
Iteration: 700; Percent complete: 17.5%; Average loss: 3.4857
Iteration: 701; Percent complete: 17.5%; Average loss: 3.6271
Iteration: 702; Percent complete: 17.5%; Average loss: 3.6304
Iteration: 703; Percent complete: 17.6%; Average loss: 3.5918
Iteration: 704; Percent complete: 17.6%; Average loss: 3.7747
Iteration: 705; Percent complete: 17.6%; Average loss: 3.5732
Iteration: 706; Percent complete: 17.6%; Average loss: 3.5330
Iteration: 707; Percent complete: 17.7%; Average loss: 3.7832
Iteration: 708; Percent complete: 17.7%; Average loss: 3.4224
Iteration: 709; Percent complete: 17.7%; Average loss: 3.6066
Iteration: 710; Percent complete: 17.8%; Average loss: 3.6024
Iteration: 711; Percent complete: 17.8%; Average loss: 3.6445
Iteration: 712; Percent complete: 17.8%; Average loss: 3.6253
Iteration: 713; Percent complete: 17.8%; Average loss: 3.6011
Iteration: 714; Percent complete: 17.8%; Average loss: 3.5211
Iteration: 715; Percent complete: 17.9%; Average loss: 3.4424
Iteration: 716; Percent complete: 17.9%; Average loss: 3.6821
Iteration: 717; Percent complete: 17.9%; Average loss: 3.6495
Iteration: 718; Percent complete: 17.9%; Average loss: 3.6874
Iteration: 719; Percent complete: 18.0%; Average loss: 3.6269
Iteration: 720; Percent complete: 18.0%; Average loss: 3.7078
Iteration: 721; Percent complete: 18.0%; Average loss: 3.5307
Iteration: 722; Percent complete: 18.1%; Average loss: 3.5121
Iteration: 723; Percent complete: 18.1%; Average loss: 3.3233
Iteration: 724; Percent complete: 18.1%; Average loss: 3.6162
Iteration: 725; Percent complete: 18.1%; Average loss: 3.4252
Iteration: 726; Percent complete: 18.1%; Average loss: 3.6597
Iteration: 727; Percent complete: 18.2%; Average loss: 3.8894
Iteration: 728; Percent complete: 18.2%; Average loss: 3.6575
Iteration: 729; Percent complete: 18.2%; Average loss: 3.6839
Iteration: 730; Percent complete: 18.2%; Average loss: 3.3362
Iteration: 731; Percent complete: 18.3%; Average loss: 3.5365
Iteration: 732; Percent complete: 18.3%; Average loss: 3.5397
Iteration: 733; Percent complete: 18.3%; Average loss: 3.6342
Iteration: 734; Percent complete: 18.4%; Average loss: 3.8832
Iteration: 735; Percent complete: 18.4%; Average loss: 3.5805
Iteration: 736; Percent complete: 18.4%; Average loss: 3.7293
Iteration: 737; Percent complete: 18.4%; Average loss: 3.4146
Iteration: 738; Percent complete: 18.4%; Average loss: 3.3367
Iteration: 739; Percent complete: 18.5%; Average loss: 3.5805
Iteration: 740; Percent complete: 18.5%; Average loss: 3.5487
Iteration: 741; Percent complete: 18.5%; Average loss: 3.4551
Iteration: 742; Percent complete: 18.6%; Average loss: 3.7259
Iteration: 743; Percent complete: 18.6%; Average loss: 3.6847
Iteration: 744; Percent complete: 18.6%; Average loss: 3.5365
Iteration: 745; Percent complete: 18.6%; Average loss: 3.7091
Iteration: 746; Percent complete: 18.6%; Average loss: 3.3672
Iteration: 747; Percent complete: 18.7%; Average loss: 3.6984
Iteration: 748; Percent complete: 18.7%; Average loss: 3.5982
Iteration: 749; Percent complete: 18.7%; Average loss: 3.5484
Iteration: 750; Percent complete: 18.8%; Average loss: 3.8154
Iteration: 751; Percent complete: 18.8%; Average loss: 3.6788
Iteration: 752; Percent complete: 18.8%; Average loss: 3.4706
Iteration: 753; Percent complete: 18.8%; Average loss: 3.6737
Iteration: 754; Percent complete: 18.9%; Average loss: 3.5531
Iteration: 755; Percent complete: 18.9%; Average loss: 3.7028
Iteration: 756; Percent complete: 18.9%; Average loss: 3.5872
Iteration: 757; Percent complete: 18.9%; Average loss: 3.7108
Iteration: 758; Percent complete: 18.9%; Average loss: 3.6960
Iteration: 759; Percent complete: 19.0%; Average loss: 3.5482
Iteration: 760; Percent complete: 19.0%; Average loss: 3.3988
Iteration: 761; Percent complete: 19.0%; Average loss: 3.5678
Iteration: 762; Percent complete: 19.1%; Average loss: 3.3863
Iteration: 763; Percent complete: 19.1%; Average loss: 3.8160
Iteration: 764; Percent complete: 19.1%; Average loss: 3.4578
Iteration: 765; Percent complete: 19.1%; Average loss: 3.7290
Iteration: 766; Percent complete: 19.1%; Average loss: 3.4265
Iteration: 767; Percent complete: 19.2%; Average loss: 3.7551
Iteration: 768; Percent complete: 19.2%; Average loss: 3.4712
Iteration: 769; Percent complete: 19.2%; Average loss: 3.3830
Iteration: 770; Percent complete: 19.2%; Average loss: 3.5299
Iteration: 771; Percent complete: 19.3%; Average loss: 3.6723
Iteration: 772; Percent complete: 19.3%; Average loss: 3.5188
Iteration: 773; Percent complete: 19.3%; Average loss: 3.7720
Iteration: 774; Percent complete: 19.4%; Average loss: 3.6715
Iteration: 775; Percent complete: 19.4%; Average loss: 3.3726
Iteration: 776; Percent complete: 19.4%; Average loss: 3.9572
Iteration: 777; Percent complete: 19.4%; Average loss: 3.3537
Iteration: 778; Percent complete: 19.4%; Average loss: 3.4321
Iteration: 779; Percent complete: 19.5%; Average loss: 3.5912
Iteration: 780; Percent complete: 19.5%; Average loss: 3.6060
Iteration: 781; Percent complete: 19.5%; Average loss: 3.5511
Iteration: 782; Percent complete: 19.6%; Average loss: 3.8173
Iteration: 783; Percent complete: 19.6%; Average loss: 3.7829
Iteration: 784; Percent complete: 19.6%; Average loss: 3.7797
Iteration: 785; Percent complete: 19.6%; Average loss: 3.4360
Iteration: 786; Percent complete: 19.7%; Average loss: 3.3013
Iteration: 787; Percent complete: 19.7%; Average loss: 3.4826
Iteration: 788; Percent complete: 19.7%; Average loss: 3.5817
Iteration: 789; Percent complete: 19.7%; Average loss: 3.6778
Iteration: 790; Percent complete: 19.8%; Average loss: 3.5716
Iteration: 791; Percent complete: 19.8%; Average loss: 3.7263
Iteration: 792; Percent complete: 19.8%; Average loss: 3.7545
Iteration: 793; Percent complete: 19.8%; Average loss: 3.3059
Iteration: 794; Percent complete: 19.9%; Average loss: 3.2877
Iteration: 795; Percent complete: 19.9%; Average loss: 3.7175
Iteration: 796; Percent complete: 19.9%; Average loss: 3.5802
Iteration: 797; Percent complete: 19.9%; Average loss: 3.3353
Iteration: 798; Percent complete: 20.0%; Average loss: 3.3839
Iteration: 799; Percent complete: 20.0%; Average loss: 3.5383
Iteration: 800; Percent complete: 20.0%; Average loss: 3.6496
Iteration: 801; Percent complete: 20.0%; Average loss: 3.4929
Iteration: 802; Percent complete: 20.1%; Average loss: 3.7592
Iteration: 803; Percent complete: 20.1%; Average loss: 3.6814
Iteration: 804; Percent complete: 20.1%; Average loss: 3.5799
Iteration: 805; Percent complete: 20.1%; Average loss: 3.7090
Iteration: 806; Percent complete: 20.2%; Average loss: 3.8749
Iteration: 807; Percent complete: 20.2%; Average loss: 3.5803
Iteration: 808; Percent complete: 20.2%; Average loss: 3.6890
Iteration: 809; Percent complete: 20.2%; Average loss: 3.5482
Iteration: 810; Percent complete: 20.2%; Average loss: 3.7676
Iteration: 811; Percent complete: 20.3%; Average loss: 3.6009
Iteration: 812; Percent complete: 20.3%; Average loss: 3.4369
Iteration: 813; Percent complete: 20.3%; Average loss: 3.5989
Iteration: 814; Percent complete: 20.3%; Average loss: 3.3001
Iteration: 815; Percent complete: 20.4%; Average loss: 3.3972
Iteration: 816; Percent complete: 20.4%; Average loss: 3.4838
Iteration: 817; Percent complete: 20.4%; Average loss: 3.7551
Iteration: 818; Percent complete: 20.4%; Average loss: 3.7941
Iteration: 819; Percent complete: 20.5%; Average loss: 3.6923
Iteration: 820; Percent complete: 20.5%; Average loss: 3.6021
Iteration: 821; Percent complete: 20.5%; Average loss: 3.4518
Iteration: 822; Percent complete: 20.5%; Average loss: 3.6136
Iteration: 823; Percent complete: 20.6%; Average loss: 3.5142
Iteration: 824; Percent complete: 20.6%; Average loss: 3.5817
Iteration: 825; Percent complete: 20.6%; Average loss: 3.6651
Iteration: 826; Percent complete: 20.6%; Average loss: 3.6192
Iteration: 827; Percent complete: 20.7%; Average loss: 3.5746
Iteration: 828; Percent complete: 20.7%; Average loss: 3.5260
Iteration: 829; Percent complete: 20.7%; Average loss: 3.8236
Iteration: 830; Percent complete: 20.8%; Average loss: 3.3523
Iteration: 831; Percent complete: 20.8%; Average loss: 3.5233
Iteration: 832; Percent complete: 20.8%; Average loss: 3.3825
Iteration: 833; Percent complete: 20.8%; Average loss: 3.6677
Iteration: 834; Percent complete: 20.8%; Average loss: 3.6706
Iteration: 835; Percent complete: 20.9%; Average loss: 3.7408
Iteration: 836; Percent complete: 20.9%; Average loss: 3.3450
Iteration: 837; Percent complete: 20.9%; Average loss: 3.6104
Iteration: 838; Percent complete: 20.9%; Average loss: 3.5437
Iteration: 839; Percent complete: 21.0%; Average loss: 3.3627
Iteration: 840; Percent complete: 21.0%; Average loss: 3.7376
Iteration: 841; Percent complete: 21.0%; Average loss: 3.5446
Iteration: 842; Percent complete: 21.1%; Average loss: 3.6669
Iteration: 843; Percent complete: 21.1%; Average loss: 3.6060
Iteration: 844; Percent complete: 21.1%; Average loss: 3.5413
Iteration: 845; Percent complete: 21.1%; Average loss: 3.7371
Iteration: 846; Percent complete: 21.1%; Average loss: 3.7147
Iteration: 847; Percent complete: 21.2%; Average loss: 3.5997
Iteration: 848; Percent complete: 21.2%; Average loss: 3.6390
Iteration: 849; Percent complete: 21.2%; Average loss: 3.4140
Iteration: 850; Percent complete: 21.2%; Average loss: 3.6290
Iteration: 851; Percent complete: 21.3%; Average loss: 3.4599
Iteration: 852; Percent complete: 21.3%; Average loss: 3.6890
Iteration: 853; Percent complete: 21.3%; Average loss: 3.6407
Iteration: 854; Percent complete: 21.3%; Average loss: 3.7457
Iteration: 855; Percent complete: 21.4%; Average loss: 3.4506
Iteration: 856; Percent complete: 21.4%; Average loss: 3.3458
Iteration: 857; Percent complete: 21.4%; Average loss: 3.3957
Iteration: 858; Percent complete: 21.4%; Average loss: 3.5115
Iteration: 859; Percent complete: 21.5%; Average loss: 3.6019
Iteration: 860; Percent complete: 21.5%; Average loss: 3.4633
Iteration: 861; Percent complete: 21.5%; Average loss: 3.5491
Iteration: 862; Percent complete: 21.6%; Average loss: 3.5364
Iteration: 863; Percent complete: 21.6%; Average loss: 3.5512
Iteration: 864; Percent complete: 21.6%; Average loss: 3.5782
Iteration: 865; Percent complete: 21.6%; Average loss: 3.2771
Iteration: 866; Percent complete: 21.6%; Average loss: 3.5957
Iteration: 867; Percent complete: 21.7%; Average loss: 3.6529
Iteration: 868; Percent complete: 21.7%; Average loss: 3.3378
Iteration: 869; Percent complete: 21.7%; Average loss: 3.9738
Iteration: 870; Percent complete: 21.8%; Average loss: 3.6004
Iteration: 871; Percent complete: 21.8%; Average loss: 3.6261
Iteration: 872; Percent complete: 21.8%; Average loss: 3.6707
Iteration: 873; Percent complete: 21.8%; Average loss: 3.4941
Iteration: 874; Percent complete: 21.9%; Average loss: 3.4215
Iteration: 875; Percent complete: 21.9%; Average loss: 3.4702
Iteration: 876; Percent complete: 21.9%; Average loss: 3.6513
Iteration: 877; Percent complete: 21.9%; Average loss: 3.7195
Iteration: 878; Percent complete: 21.9%; Average loss: 3.6436
Iteration: 879; Percent complete: 22.0%; Average loss: 3.4944
Iteration: 880; Percent complete: 22.0%; Average loss: 3.3708
Iteration: 881; Percent complete: 22.0%; Average loss: 3.3650
Iteration: 882; Percent complete: 22.1%; Average loss: 3.4874
Iteration: 883; Percent complete: 22.1%; Average loss: 3.3529
Iteration: 884; Percent complete: 22.1%; Average loss: 3.4552
Iteration: 885; Percent complete: 22.1%; Average loss: 3.5784
Iteration: 886; Percent complete: 22.1%; Average loss: 3.5234
Iteration: 887; Percent complete: 22.2%; Average loss: 3.3666
Iteration: 888; Percent complete: 22.2%; Average loss: 3.5268
Iteration: 889; Percent complete: 22.2%; Average loss: 3.5002
Iteration: 890; Percent complete: 22.2%; Average loss: 3.2712
Iteration: 891; Percent complete: 22.3%; Average loss: 3.4187
Iteration: 892; Percent complete: 22.3%; Average loss: 3.6959
Iteration: 893; Percent complete: 22.3%; Average loss: 3.4804
Iteration: 894; Percent complete: 22.4%; Average loss: 3.4998
Iteration: 895; Percent complete: 22.4%; Average loss: 3.4241
Iteration: 896; Percent complete: 22.4%; Average loss: 3.5072
Iteration: 897; Percent complete: 22.4%; Average loss: 3.5320
Iteration: 898; Percent complete: 22.4%; Average loss: 3.4120
Iteration: 899; Percent complete: 22.5%; Average loss: 3.4997
Iteration: 900; Percent complete: 22.5%; Average loss: 3.8357
Iteration: 901; Percent complete: 22.5%; Average loss: 3.4580
Iteration: 902; Percent complete: 22.6%; Average loss: 4.0026
Iteration: 903; Percent complete: 22.6%; Average loss: 3.6159
Iteration: 904; Percent complete: 22.6%; Average loss: 3.6930
Iteration: 905; Percent complete: 22.6%; Average loss: 3.5995
Iteration: 906; Percent complete: 22.7%; Average loss: 3.7818
Iteration: 907; Percent complete: 22.7%; Average loss: 3.6158
Iteration: 908; Percent complete: 22.7%; Average loss: 3.2371
Iteration: 909; Percent complete: 22.7%; Average loss: 3.7979
Iteration: 910; Percent complete: 22.8%; Average loss: 3.5951
Iteration: 911; Percent complete: 22.8%; Average loss: 3.2562
Iteration: 912; Percent complete: 22.8%; Average loss: 3.7380
Iteration: 913; Percent complete: 22.8%; Average loss: 3.3552
Iteration: 914; Percent complete: 22.9%; Average loss: 3.7924
Iteration: 915; Percent complete: 22.9%; Average loss: 3.5297
Iteration: 916; Percent complete: 22.9%; Average loss: 3.4356
Iteration: 917; Percent complete: 22.9%; Average loss: 3.5926
Iteration: 918; Percent complete: 22.9%; Average loss: 3.5818
Iteration: 919; Percent complete: 23.0%; Average loss: 3.5979
Iteration: 920; Percent complete: 23.0%; Average loss: 3.6661
Iteration: 921; Percent complete: 23.0%; Average loss: 3.4307
Iteration: 922; Percent complete: 23.1%; Average loss: 3.5885
Iteration: 923; Percent complete: 23.1%; Average loss: 3.2140
Iteration: 924; Percent complete: 23.1%; Average loss: 3.1408
Iteration: 925; Percent complete: 23.1%; Average loss: 3.6595
Iteration: 926; Percent complete: 23.2%; Average loss: 3.2236
Iteration: 927; Percent complete: 23.2%; Average loss: 3.6086
Iteration: 928; Percent complete: 23.2%; Average loss: 3.5783
Iteration: 929; Percent complete: 23.2%; Average loss: 3.5513
Iteration: 930; Percent complete: 23.2%; Average loss: 3.6069
Iteration: 931; Percent complete: 23.3%; Average loss: 3.4164
Iteration: 932; Percent complete: 23.3%; Average loss: 3.6508
Iteration: 933; Percent complete: 23.3%; Average loss: 3.5856
Iteration: 934; Percent complete: 23.4%; Average loss: 3.5492
Iteration: 935; Percent complete: 23.4%; Average loss: 3.3671
Iteration: 936; Percent complete: 23.4%; Average loss: 3.4014
Iteration: 937; Percent complete: 23.4%; Average loss: 3.3963
Iteration: 938; Percent complete: 23.4%; Average loss: 3.7436
Iteration: 939; Percent complete: 23.5%; Average loss: 3.5940
Iteration: 940; Percent complete: 23.5%; Average loss: 3.4050
Iteration: 941; Percent complete: 23.5%; Average loss: 3.5344
Iteration: 942; Percent complete: 23.5%; Average loss: 3.6279
Iteration: 943; Percent complete: 23.6%; Average loss: 3.3849
Iteration: 944; Percent complete: 23.6%; Average loss: 3.5922
Iteration: 945; Percent complete: 23.6%; Average loss: 3.3878
Iteration: 946; Percent complete: 23.6%; Average loss: 3.4188
Iteration: 947; Percent complete: 23.7%; Average loss: 3.6332
Iteration: 948; Percent complete: 23.7%; Average loss: 3.6788
Iteration: 949; Percent complete: 23.7%; Average loss: 3.4900
Iteration: 950; Percent complete: 23.8%; Average loss: 3.3522
Iteration: 951; Percent complete: 23.8%; Average loss: 3.4179
Iteration: 952; Percent complete: 23.8%; Average loss: 3.5544
Iteration: 953; Percent complete: 23.8%; Average loss: 3.4232
Iteration: 954; Percent complete: 23.8%; Average loss: 3.3613
Iteration: 955; Percent complete: 23.9%; Average loss: 3.6074
Iteration: 956; Percent complete: 23.9%; Average loss: 3.3591
Iteration: 957; Percent complete: 23.9%; Average loss: 3.6687
Iteration: 958; Percent complete: 23.9%; Average loss: 3.3270
Iteration: 959; Percent complete: 24.0%; Average loss: 3.7049
Iteration: 960; Percent complete: 24.0%; Average loss: 3.5652
Iteration: 961; Percent complete: 24.0%; Average loss: 3.5806
Iteration: 962; Percent complete: 24.1%; Average loss: 3.5142
Iteration: 963; Percent complete: 24.1%; Average loss: 3.4120
Iteration: 964; Percent complete: 24.1%; Average loss: 3.5846
Iteration: 965; Percent complete: 24.1%; Average loss: 3.3704
Iteration: 966; Percent complete: 24.1%; Average loss: 3.3542
Iteration: 967; Percent complete: 24.2%; Average loss: 3.3730
Iteration: 968; Percent complete: 24.2%; Average loss: 3.5125
Iteration: 969; Percent complete: 24.2%; Average loss: 3.2609
Iteration: 970; Percent complete: 24.2%; Average loss: 3.1309
Iteration: 971; Percent complete: 24.3%; Average loss: 3.6205
Iteration: 972; Percent complete: 24.3%; Average loss: 3.5793
Iteration: 973; Percent complete: 24.3%; Average loss: 3.6798
Iteration: 974; Percent complete: 24.3%; Average loss: 3.6167
Iteration: 975; Percent complete: 24.4%; Average loss: 3.6184
Iteration: 976; Percent complete: 24.4%; Average loss: 3.5397
Iteration: 977; Percent complete: 24.4%; Average loss: 3.6041
Iteration: 978; Percent complete: 24.4%; Average loss: 3.5801
Iteration: 979; Percent complete: 24.5%; Average loss: 3.5486
Iteration: 980; Percent complete: 24.5%; Average loss: 3.5581
Iteration: 981; Percent complete: 24.5%; Average loss: 3.4954
Iteration: 982; Percent complete: 24.6%; Average loss: 3.4253
Iteration: 983; Percent complete: 24.6%; Average loss: 3.5679
Iteration: 984; Percent complete: 24.6%; Average loss: 3.6388
Iteration: 985; Percent complete: 24.6%; Average loss: 3.4385
Iteration: 986; Percent complete: 24.6%; Average loss: 3.3518
Iteration: 987; Percent complete: 24.7%; Average loss: 3.4705
Iteration: 988; Percent complete: 24.7%; Average loss: 3.6166
Iteration: 989; Percent complete: 24.7%; Average loss: 3.5864
Iteration: 990; Percent complete: 24.8%; Average loss: 3.2577
Iteration: 991; Percent complete: 24.8%; Average loss: 3.4349
Iteration: 992; Percent complete: 24.8%; Average loss: 3.1997
Iteration: 993; Percent complete: 24.8%; Average loss: 3.5636
Iteration: 994; Percent complete: 24.9%; Average loss: 3.4838
Iteration: 995; Percent complete: 24.9%; Average loss: 3.6398
Iteration: 996; Percent complete: 24.9%; Average loss: 3.5966
Iteration: 997; Percent complete: 24.9%; Average loss: 3.8269
Iteration: 998; Percent complete: 24.9%; Average loss: 3.4513
Iteration: 999; Percent complete: 25.0%; Average loss: 3.3553
Iteration: 1000; Percent complete: 25.0%; Average loss: 3.6312
Iteration: 1001; Percent complete: 25.0%; Average loss: 3.5302
Iteration: 1002; Percent complete: 25.1%; Average loss: 3.3474
Iteration: 1003; Percent complete: 25.1%; Average loss: 3.5402
Iteration: 1004; Percent complete: 25.1%; Average loss: 3.2926
Iteration: 1005; Percent complete: 25.1%; Average loss: 3.5181
Iteration: 1006; Percent complete: 25.1%; Average loss: 3.3389
Iteration: 1007; Percent complete: 25.2%; Average loss: 3.4523
Iteration: 1008; Percent complete: 25.2%; Average loss: 3.5193
Iteration: 1009; Percent complete: 25.2%; Average loss: 3.3489
Iteration: 1010; Percent complete: 25.2%; Average loss: 3.4856
Iteration: 1011; Percent complete: 25.3%; Average loss: 3.2742
Iteration: 1012; Percent complete: 25.3%; Average loss: 3.5170
Iteration: 1013; Percent complete: 25.3%; Average loss: 3.3525
Iteration: 1014; Percent complete: 25.4%; Average loss: 3.5976
Iteration: 1015; Percent complete: 25.4%; Average loss: 3.2216
Iteration: 1016; Percent complete: 25.4%; Average loss: 3.6466
Iteration: 1017; Percent complete: 25.4%; Average loss: 3.6863
Iteration: 1018; Percent complete: 25.4%; Average loss: 3.4186
Iteration: 1019; Percent complete: 25.5%; Average loss: 3.3721
Iteration: 1020; Percent complete: 25.5%; Average loss: 3.3032
Iteration: 1021; Percent complete: 25.5%; Average loss: 3.3491
Iteration: 1022; Percent complete: 25.6%; Average loss: 3.3338
Iteration: 1023; Percent complete: 25.6%; Average loss: 3.6505
Iteration: 1024; Percent complete: 25.6%; Average loss: 3.4090
Iteration: 1025; Percent complete: 25.6%; Average loss: 3.2392
Iteration: 1026; Percent complete: 25.7%; Average loss: 3.5784
Iteration: 1027; Percent complete: 25.7%; Average loss: 3.5433
Iteration: 1028; Percent complete: 25.7%; Average loss: 3.5900
Iteration: 1029; Percent complete: 25.7%; Average loss: 3.7796
Iteration: 1030; Percent complete: 25.8%; Average loss: 3.4986
Iteration: 1031; Percent complete: 25.8%; Average loss: 3.2436
Iteration: 1032; Percent complete: 25.8%; Average loss: 3.2657
Iteration: 1033; Percent complete: 25.8%; Average loss: 3.5024
Iteration: 1034; Percent complete: 25.9%; Average loss: 3.5557
Iteration: 1035; Percent complete: 25.9%; Average loss: 3.4302
Iteration: 1036; Percent complete: 25.9%; Average loss: 3.3372
Iteration: 1037; Percent complete: 25.9%; Average loss: 3.2322
Iteration: 1038; Percent complete: 25.9%; Average loss: 3.5489
Iteration: 1039; Percent complete: 26.0%; Average loss: 3.5201
Iteration: 1040; Percent complete: 26.0%; Average loss: 3.3084
Iteration: 1041; Percent complete: 26.0%; Average loss: 3.4168
Iteration: 1042; Percent complete: 26.1%; Average loss: 3.3519
Iteration: 1043; Percent complete: 26.1%; Average loss: 3.7866
Iteration: 1044; Percent complete: 26.1%; Average loss: 3.3692
Iteration: 1045; Percent complete: 26.1%; Average loss: 3.5977
Iteration: 1046; Percent complete: 26.2%; Average loss: 3.7003
Iteration: 1047; Percent complete: 26.2%; Average loss: 3.5318
Iteration: 1048; Percent complete: 26.2%; Average loss: 3.5779
Iteration: 1049; Percent complete: 26.2%; Average loss: 3.5905
Iteration: 1050; Percent complete: 26.2%; Average loss: 3.5117
Iteration: 1051; Percent complete: 26.3%; Average loss: 3.3647
Iteration: 1052; Percent complete: 26.3%; Average loss: 3.3093
Iteration: 1053; Percent complete: 26.3%; Average loss: 3.5096
Iteration: 1054; Percent complete: 26.4%; Average loss: 3.3405
Iteration: 1055; Percent complete: 26.4%; Average loss: 3.3941
Iteration: 1056; Percent complete: 26.4%; Average loss: 3.3783
Iteration: 1057; Percent complete: 26.4%; Average loss: 3.6120
Iteration: 1058; Percent complete: 26.5%; Average loss: 3.5988
Iteration: 1059; Percent complete: 26.5%; Average loss: 3.2916
Iteration: 1060; Percent complete: 26.5%; Average loss: 3.3281
Iteration: 1061; Percent complete: 26.5%; Average loss: 3.1558
Iteration: 1062; Percent complete: 26.6%; Average loss: 3.2074
Iteration: 1063; Percent complete: 26.6%; Average loss: 3.3973
Iteration: 1064; Percent complete: 26.6%; Average loss: 3.4148
Iteration: 1065; Percent complete: 26.6%; Average loss: 3.3236
Iteration: 1066; Percent complete: 26.7%; Average loss: 3.5764
Iteration: 1067; Percent complete: 26.7%; Average loss: 3.5348
Iteration: 1068; Percent complete: 26.7%; Average loss: 3.4083
Iteration: 1069; Percent complete: 26.7%; Average loss: 3.3404
Iteration: 1070; Percent complete: 26.8%; Average loss: 3.5471
Iteration: 1071; Percent complete: 26.8%; Average loss: 3.4237
Iteration: 1072; Percent complete: 26.8%; Average loss: 3.3313
Iteration: 1073; Percent complete: 26.8%; Average loss: 3.1475
Iteration: 1074; Percent complete: 26.9%; Average loss: 3.3946
Iteration: 1075; Percent complete: 26.9%; Average loss: 3.6507
Iteration: 1076; Percent complete: 26.9%; Average loss: 3.1790
Iteration: 1077; Percent complete: 26.9%; Average loss: 3.5596
Iteration: 1078; Percent complete: 27.0%; Average loss: 3.5537
Iteration: 1079; Percent complete: 27.0%; Average loss: 3.2612
Iteration: 1080; Percent complete: 27.0%; Average loss: 3.5206
Iteration: 1081; Percent complete: 27.0%; Average loss: 3.4390
Iteration: 1082; Percent complete: 27.1%; Average loss: 3.1888
Iteration: 1083; Percent complete: 27.1%; Average loss: 3.4194
Iteration: 1084; Percent complete: 27.1%; Average loss: 3.4800
Iteration: 1085; Percent complete: 27.1%; Average loss: 3.3975
Iteration: 1086; Percent complete: 27.2%; Average loss: 3.5940
Iteration: 1087; Percent complete: 27.2%; Average loss: 3.5048
Iteration: 1088; Percent complete: 27.2%; Average loss: 3.4297
Iteration: 1089; Percent complete: 27.2%; Average loss: 3.4989
Iteration: 1090; Percent complete: 27.3%; Average loss: 3.8013
Iteration: 1091; Percent complete: 27.3%; Average loss: 3.4981
Iteration: 1092; Percent complete: 27.3%; Average loss: 3.4089
Iteration: 1093; Percent complete: 27.3%; Average loss: 3.8070
Iteration: 1094; Percent complete: 27.4%; Average loss: 3.4768
Iteration: 1095; Percent complete: 27.4%; Average loss: 3.3063
Iteration: 1096; Percent complete: 27.4%; Average loss: 3.3933
Iteration: 1097; Percent complete: 27.4%; Average loss: 3.5759
Iteration: 1098; Percent complete: 27.5%; Average loss: 3.4270
Iteration: 1099; Percent complete: 27.5%; Average loss: 3.3384
Iteration: 1100; Percent complete: 27.5%; Average loss: 3.3956
Iteration: 1101; Percent complete: 27.5%; Average loss: 3.4487
Iteration: 1102; Percent complete: 27.6%; Average loss: 3.5772
Iteration: 1103; Percent complete: 27.6%; Average loss: 3.4364
Iteration: 1104; Percent complete: 27.6%; Average loss: 3.5478
Iteration: 1105; Percent complete: 27.6%; Average loss: 3.2119
Iteration: 1106; Percent complete: 27.7%; Average loss: 3.3052
Iteration: 1107; Percent complete: 27.7%; Average loss: 3.2968
Iteration: 1108; Percent complete: 27.7%; Average loss: 3.3336
Iteration: 1109; Percent complete: 27.7%; Average loss: 3.4881
Iteration: 1110; Percent complete: 27.8%; Average loss: 3.3545
Iteration: 1111; Percent complete: 27.8%; Average loss: 3.4650
Iteration: 1112; Percent complete: 27.8%; Average loss: 3.3334
Iteration: 1113; Percent complete: 27.8%; Average loss: 3.3202
Iteration: 1114; Percent complete: 27.9%; Average loss: 3.1362
Iteration: 1115; Percent complete: 27.9%; Average loss: 3.3218
Iteration: 1116; Percent complete: 27.9%; Average loss: 3.5457
Iteration: 1117; Percent complete: 27.9%; Average loss: 3.3814
Iteration: 1118; Percent complete: 28.0%; Average loss: 3.8046
Iteration: 1119; Percent complete: 28.0%; Average loss: 3.2408
Iteration: 1120; Percent complete: 28.0%; Average loss: 3.6691
Iteration: 1121; Percent complete: 28.0%; Average loss: 3.8136
Iteration: 1122; Percent complete: 28.1%; Average loss: 3.3725
Iteration: 1123; Percent complete: 28.1%; Average loss: 3.4894
Iteration: 1124; Percent complete: 28.1%; Average loss: 3.2555
Iteration: 1125; Percent complete: 28.1%; Average loss: 3.4534
Iteration: 1126; Percent complete: 28.1%; Average loss: 3.2749
Iteration: 1127; Percent complete: 28.2%; Average loss: 3.9222
Iteration: 1128; Percent complete: 28.2%; Average loss: 3.2617
Iteration: 1129; Percent complete: 28.2%; Average loss: 3.3749
Iteration: 1130; Percent complete: 28.2%; Average loss: 3.2620
Iteration: 1131; Percent complete: 28.3%; Average loss: 3.3392
Iteration: 1132; Percent complete: 28.3%; Average loss: 3.5340
Iteration: 1133; Percent complete: 28.3%; Average loss: 3.5638
Iteration: 1134; Percent complete: 28.3%; Average loss: 3.4144
Iteration: 1135; Percent complete: 28.4%; Average loss: 3.4780
Iteration: 1136; Percent complete: 28.4%; Average loss: 3.2765
Iteration: 1137; Percent complete: 28.4%; Average loss: 3.3590
Iteration: 1138; Percent complete: 28.4%; Average loss: 3.3057
Iteration: 1139; Percent complete: 28.5%; Average loss: 3.0906
Iteration: 1140; Percent complete: 28.5%; Average loss: 3.1117
Iteration: 1141; Percent complete: 28.5%; Average loss: 3.5874
Iteration: 1142; Percent complete: 28.5%; Average loss: 3.5694
Iteration: 1143; Percent complete: 28.6%; Average loss: 3.6386
Iteration: 1144; Percent complete: 28.6%; Average loss: 3.3642
Iteration: 1145; Percent complete: 28.6%; Average loss: 3.3464
Iteration: 1146; Percent complete: 28.6%; Average loss: 3.4684
Iteration: 1147; Percent complete: 28.7%; Average loss: 3.2372
Iteration: 1148; Percent complete: 28.7%; Average loss: 3.3236
Iteration: 1149; Percent complete: 28.7%; Average loss: 3.6791
Iteration: 1150; Percent complete: 28.7%; Average loss: 3.3972
Iteration: 1151; Percent complete: 28.8%; Average loss: 3.2514
Iteration: 1152; Percent complete: 28.8%; Average loss: 3.4142
Iteration: 1153; Percent complete: 28.8%; Average loss: 3.4110
Iteration: 1154; Percent complete: 28.8%; Average loss: 3.6695
Iteration: 1155; Percent complete: 28.9%; Average loss: 3.3998
Iteration: 1156; Percent complete: 28.9%; Average loss: 3.3277
Iteration: 1157; Percent complete: 28.9%; Average loss: 3.4743
Iteration: 1158; Percent complete: 28.9%; Average loss: 3.3418
Iteration: 1159; Percent complete: 29.0%; Average loss: 3.4306
Iteration: 1160; Percent complete: 29.0%; Average loss: 3.3544
Iteration: 1161; Percent complete: 29.0%; Average loss: 3.4412
Iteration: 1162; Percent complete: 29.0%; Average loss: 3.6073
Iteration: 1163; Percent complete: 29.1%; Average loss: 3.5156
Iteration: 1164; Percent complete: 29.1%; Average loss: 3.3223
Iteration: 1165; Percent complete: 29.1%; Average loss: 3.1036
Iteration: 1166; Percent complete: 29.1%; Average loss: 3.3273
Iteration: 1167; Percent complete: 29.2%; Average loss: 3.5744
Iteration: 1168; Percent complete: 29.2%; Average loss: 3.6263
Iteration: 1169; Percent complete: 29.2%; Average loss: 3.4610
Iteration: 1170; Percent complete: 29.2%; Average loss: 3.4711
Iteration: 1171; Percent complete: 29.3%; Average loss: 3.4350
Iteration: 1172; Percent complete: 29.3%; Average loss: 3.3495
Iteration: 1173; Percent complete: 29.3%; Average loss: 3.6178
Iteration: 1174; Percent complete: 29.3%; Average loss: 3.2603
Iteration: 1175; Percent complete: 29.4%; Average loss: 3.4032
Iteration: 1176; Percent complete: 29.4%; Average loss: 3.3269
Iteration: 1177; Percent complete: 29.4%; Average loss: 3.6458
Iteration: 1178; Percent complete: 29.4%; Average loss: 3.3296
Iteration: 1179; Percent complete: 29.5%; Average loss: 3.4189
Iteration: 1180; Percent complete: 29.5%; Average loss: 3.2839
Iteration: 1181; Percent complete: 29.5%; Average loss: 3.6018
Iteration: 1182; Percent complete: 29.5%; Average loss: 3.3902
Iteration: 1183; Percent complete: 29.6%; Average loss: 3.4555
Iteration: 1184; Percent complete: 29.6%; Average loss: 3.5109
Iteration: 1185; Percent complete: 29.6%; Average loss: 3.3108
Iteration: 1186; Percent complete: 29.6%; Average loss: 3.2295
Iteration: 1187; Percent complete: 29.7%; Average loss: 3.4656
Iteration: 1188; Percent complete: 29.7%; Average loss: 3.5755
Iteration: 1189; Percent complete: 29.7%; Average loss: 3.4949
Iteration: 1190; Percent complete: 29.8%; Average loss: 3.2540
Iteration: 1191; Percent complete: 29.8%; Average loss: 3.2358
Iteration: 1192; Percent complete: 29.8%; Average loss: 3.2405
Iteration: 1193; Percent complete: 29.8%; Average loss: 3.5303
Iteration: 1194; Percent complete: 29.8%; Average loss: 3.3098
Iteration: 1195; Percent complete: 29.9%; Average loss: 3.5519
Iteration: 1196; Percent complete: 29.9%; Average loss: 3.2687
Iteration: 1197; Percent complete: 29.9%; Average loss: 3.9230
Iteration: 1198; Percent complete: 29.9%; Average loss: 3.1198
Iteration: 1199; Percent complete: 30.0%; Average loss: 3.3798
Iteration: 1200; Percent complete: 30.0%; Average loss: 3.1252
Iteration: 1201; Percent complete: 30.0%; Average loss: 3.8068
Iteration: 1202; Percent complete: 30.0%; Average loss: 3.2635
Iteration: 1203; Percent complete: 30.1%; Average loss: 3.1617
Iteration: 1204; Percent complete: 30.1%; Average loss: 3.4029
Iteration: 1205; Percent complete: 30.1%; Average loss: 3.2109
Iteration: 1206; Percent complete: 30.1%; Average loss: 3.2685
Iteration: 1207; Percent complete: 30.2%; Average loss: 3.2202
Iteration: 1208; Percent complete: 30.2%; Average loss: 3.4500
Iteration: 1209; Percent complete: 30.2%; Average loss: 3.4373
Iteration: 1210; Percent complete: 30.2%; Average loss: 3.1642
Iteration: 1211; Percent complete: 30.3%; Average loss: 3.2802
Iteration: 1212; Percent complete: 30.3%; Average loss: 3.8917
Iteration: 1213; Percent complete: 30.3%; Average loss: 3.4839
Iteration: 1214; Percent complete: 30.3%; Average loss: 3.6535
Iteration: 1215; Percent complete: 30.4%; Average loss: 3.4716
Iteration: 1216; Percent complete: 30.4%; Average loss: 3.4500
Iteration: 1217; Percent complete: 30.4%; Average loss: 3.3758
Iteration: 1218; Percent complete: 30.4%; Average loss: 3.7435
Iteration: 1219; Percent complete: 30.5%; Average loss: 3.2252
Iteration: 1220; Percent complete: 30.5%; Average loss: 3.3844
Iteration: 1221; Percent complete: 30.5%; Average loss: 3.4481
Iteration: 1222; Percent complete: 30.6%; Average loss: 3.4401
Iteration: 1223; Percent complete: 30.6%; Average loss: 3.6328
Iteration: 1224; Percent complete: 30.6%; Average loss: 3.2793
Iteration: 1225; Percent complete: 30.6%; Average loss: 3.5352
Iteration: 1226; Percent complete: 30.6%; Average loss: 3.2450
Iteration: 1227; Percent complete: 30.7%; Average loss: 3.3145
Iteration: 1228; Percent complete: 30.7%; Average loss: 3.3457
Iteration: 1229; Percent complete: 30.7%; Average loss: 3.2649
Iteration: 1230; Percent complete: 30.8%; Average loss: 3.4161
Iteration: 1231; Percent complete: 30.8%; Average loss: 3.3385
Iteration: 1232; Percent complete: 30.8%; Average loss: 3.3157
Iteration: 1233; Percent complete: 30.8%; Average loss: 3.4053
Iteration: 1234; Percent complete: 30.9%; Average loss: 3.3846
Iteration: 1235; Percent complete: 30.9%; Average loss: 3.5183
Iteration: 1236; Percent complete: 30.9%; Average loss: 3.3970
Iteration: 1237; Percent complete: 30.9%; Average loss: 3.3315
Iteration: 1238; Percent complete: 30.9%; Average loss: 3.3031
Iteration: 1239; Percent complete: 31.0%; Average loss: 3.4274
Iteration: 1240; Percent complete: 31.0%; Average loss: 3.2885
Iteration: 1241; Percent complete: 31.0%; Average loss: 3.2368
Iteration: 1242; Percent complete: 31.1%; Average loss: 3.5376
Iteration: 1243; Percent complete: 31.1%; Average loss: 3.3342
Iteration: 1244; Percent complete: 31.1%; Average loss: 3.5952
Iteration: 1245; Percent complete: 31.1%; Average loss: 3.4978
Iteration: 1246; Percent complete: 31.1%; Average loss: 3.6358
Iteration: 1247; Percent complete: 31.2%; Average loss: 3.4617
Iteration: 1248; Percent complete: 31.2%; Average loss: 3.1822
Iteration: 1249; Percent complete: 31.2%; Average loss: 3.3890
Iteration: 1250; Percent complete: 31.2%; Average loss: 3.3190
Iteration: 1251; Percent complete: 31.3%; Average loss: 3.3645
Iteration: 1252; Percent complete: 31.3%; Average loss: 3.5600
Iteration: 1253; Percent complete: 31.3%; Average loss: 3.5509
Iteration: 1254; Percent complete: 31.4%; Average loss: 3.4738
Iteration: 1255; Percent complete: 31.4%; Average loss: 3.4074
Iteration: 1256; Percent complete: 31.4%; Average loss: 3.6552
Iteration: 1257; Percent complete: 31.4%; Average loss: 3.2292
Iteration: 1258; Percent complete: 31.4%; Average loss: 3.3130
Iteration: 1259; Percent complete: 31.5%; Average loss: 3.4069
Iteration: 1260; Percent complete: 31.5%; Average loss: 3.3124
Iteration: 1261; Percent complete: 31.5%; Average loss: 3.4225
Iteration: 1262; Percent complete: 31.6%; Average loss: 3.3450
Iteration: 1263; Percent complete: 31.6%; Average loss: 3.4801
Iteration: 1264; Percent complete: 31.6%; Average loss: 3.2223
Iteration: 1265; Percent complete: 31.6%; Average loss: 3.4339
Iteration: 1266; Percent complete: 31.6%; Average loss: 3.2886
Iteration: 1267; Percent complete: 31.7%; Average loss: 3.2483
Iteration: 1268; Percent complete: 31.7%; Average loss: 3.0972
Iteration: 1269; Percent complete: 31.7%; Average loss: 3.2392
Iteration: 1270; Percent complete: 31.8%; Average loss: 3.3237
Iteration: 1271; Percent complete: 31.8%; Average loss: 3.3933
Iteration: 1272; Percent complete: 31.8%; Average loss: 3.2772
Iteration: 1273; Percent complete: 31.8%; Average loss: 3.3238
Iteration: 1274; Percent complete: 31.9%; Average loss: 3.2988
Iteration: 1275; Percent complete: 31.9%; Average loss: 3.4060
Iteration: 1276; Percent complete: 31.9%; Average loss: 3.4682
Iteration: 1277; Percent complete: 31.9%; Average loss: 3.4280
Iteration: 1278; Percent complete: 31.9%; Average loss: 3.6538
Iteration: 1279; Percent complete: 32.0%; Average loss: 3.7291
Iteration: 1280; Percent complete: 32.0%; Average loss: 3.4775
Iteration: 1281; Percent complete: 32.0%; Average loss: 3.3723
Iteration: 1282; Percent complete: 32.0%; Average loss: 3.2490
Iteration: 1283; Percent complete: 32.1%; Average loss: 3.4619
Iteration: 1284; Percent complete: 32.1%; Average loss: 3.4684
Iteration: 1285; Percent complete: 32.1%; Average loss: 3.4294
Iteration: 1286; Percent complete: 32.1%; Average loss: 3.3940
Iteration: 1287; Percent complete: 32.2%; Average loss: 3.5259
Iteration: 1288; Percent complete: 32.2%; Average loss: 3.2248
Iteration: 1289; Percent complete: 32.2%; Average loss: 3.2293
Iteration: 1290; Percent complete: 32.2%; Average loss: 3.5637
Iteration: 1291; Percent complete: 32.3%; Average loss: 3.0632
Iteration: 1292; Percent complete: 32.3%; Average loss: 3.4506
Iteration: 1293; Percent complete: 32.3%; Average loss: 3.8784
Iteration: 1294; Percent complete: 32.4%; Average loss: 3.2213
Iteration: 1295; Percent complete: 32.4%; Average loss: 3.6025
Iteration: 1296; Percent complete: 32.4%; Average loss: 3.3302
Iteration: 1297; Percent complete: 32.4%; Average loss: 3.1028
Iteration: 1298; Percent complete: 32.5%; Average loss: 3.2190
Iteration: 1299; Percent complete: 32.5%; Average loss: 2.9064
Iteration: 1300; Percent complete: 32.5%; Average loss: 3.2827
Iteration: 1301; Percent complete: 32.5%; Average loss: 3.3107
Iteration: 1302; Percent complete: 32.6%; Average loss: 3.3227
Iteration: 1303; Percent complete: 32.6%; Average loss: 3.5702
Iteration: 1304; Percent complete: 32.6%; Average loss: 3.2893
Iteration: 1305; Percent complete: 32.6%; Average loss: 3.3483
Iteration: 1306; Percent complete: 32.6%; Average loss: 3.4333
Iteration: 1307; Percent complete: 32.7%; Average loss: 3.2612
Iteration: 1308; Percent complete: 32.7%; Average loss: 3.2886
Iteration: 1309; Percent complete: 32.7%; Average loss: 3.3163
Iteration: 1310; Percent complete: 32.8%; Average loss: 3.4794
Iteration: 1311; Percent complete: 32.8%; Average loss: 3.5156
Iteration: 1312; Percent complete: 32.8%; Average loss: 3.4440
Iteration: 1313; Percent complete: 32.8%; Average loss: 3.4199
Iteration: 1314; Percent complete: 32.9%; Average loss: 3.4761
Iteration: 1315; Percent complete: 32.9%; Average loss: 3.4433
Iteration: 1316; Percent complete: 32.9%; Average loss: 3.3975
Iteration: 1317; Percent complete: 32.9%; Average loss: 3.2535
Iteration: 1318; Percent complete: 33.0%; Average loss: 3.1940
Iteration: 1319; Percent complete: 33.0%; Average loss: 3.3734
Iteration: 1320; Percent complete: 33.0%; Average loss: 3.4299
Iteration: 1321; Percent complete: 33.0%; Average loss: 3.5046
Iteration: 1322; Percent complete: 33.1%; Average loss: 3.5495
Iteration: 1323; Percent complete: 33.1%; Average loss: 3.2804
Iteration: 1324; Percent complete: 33.1%; Average loss: 3.6033
Iteration: 1325; Percent complete: 33.1%; Average loss: 3.3440
Iteration: 1326; Percent complete: 33.1%; Average loss: 3.3970
Iteration: 1327; Percent complete: 33.2%; Average loss: 3.4864
Iteration: 1328; Percent complete: 33.2%; Average loss: 3.3965
Iteration: 1329; Percent complete: 33.2%; Average loss: 3.5240
Iteration: 1330; Percent complete: 33.2%; Average loss: 3.1536
Iteration: 1331; Percent complete: 33.3%; Average loss: 3.4256
Iteration: 1332; Percent complete: 33.3%; Average loss: 3.2987
Iteration: 1333; Percent complete: 33.3%; Average loss: 3.2320
Iteration: 1334; Percent complete: 33.4%; Average loss: 3.3189
Iteration: 1335; Percent complete: 33.4%; Average loss: 3.2216
Iteration: 1336; Percent complete: 33.4%; Average loss: 3.4930
Iteration: 1337; Percent complete: 33.4%; Average loss: 3.2895
Iteration: 1338; Percent complete: 33.5%; Average loss: 3.3999
Iteration: 1339; Percent complete: 33.5%; Average loss: 3.3092
Iteration: 1340; Percent complete: 33.5%; Average loss: 3.2494
Iteration: 1341; Percent complete: 33.5%; Average loss: 3.5383
Iteration: 1342; Percent complete: 33.6%; Average loss: 3.1859
Iteration: 1343; Percent complete: 33.6%; Average loss: 3.1861
Iteration: 1344; Percent complete: 33.6%; Average loss: 3.1653
Iteration: 1345; Percent complete: 33.6%; Average loss: 3.2298
Iteration: 1346; Percent complete: 33.7%; Average loss: 3.3653
Iteration: 1347; Percent complete: 33.7%; Average loss: 3.1742
Iteration: 1348; Percent complete: 33.7%; Average loss: 3.4260
Iteration: 1349; Percent complete: 33.7%; Average loss: 3.3700
Iteration: 1350; Percent complete: 33.8%; Average loss: 3.1388
Iteration: 1351; Percent complete: 33.8%; Average loss: 3.4001
Iteration: 1352; Percent complete: 33.8%; Average loss: 3.6088
Iteration: 1353; Percent complete: 33.8%; Average loss: 3.3862
Iteration: 1354; Percent complete: 33.9%; Average loss: 3.5094
Iteration: 1355; Percent complete: 33.9%; Average loss: 3.3479
Iteration: 1356; Percent complete: 33.9%; Average loss: 3.3448
Iteration: 1357; Percent complete: 33.9%; Average loss: 3.2086
Iteration: 1358; Percent complete: 34.0%; Average loss: 3.4434
Iteration: 1359; Percent complete: 34.0%; Average loss: 3.3838
Iteration: 1360; Percent complete: 34.0%; Average loss: 3.3528
Iteration: 1361; Percent complete: 34.0%; Average loss: 3.5188
Iteration: 1362; Percent complete: 34.1%; Average loss: 3.2308
Iteration: 1363; Percent complete: 34.1%; Average loss: 3.2991
Iteration: 1364; Percent complete: 34.1%; Average loss: 3.6166
Iteration: 1365; Percent complete: 34.1%; Average loss: 3.2833
Iteration: 1366; Percent complete: 34.2%; Average loss: 3.7807
Iteration: 1367; Percent complete: 34.2%; Average loss: 3.2043
Iteration: 1368; Percent complete: 34.2%; Average loss: 3.2147
Iteration: 1369; Percent complete: 34.2%; Average loss: 3.2576
Iteration: 1370; Percent complete: 34.2%; Average loss: 3.3312
Iteration: 1371; Percent complete: 34.3%; Average loss: 3.0938
Iteration: 1372; Percent complete: 34.3%; Average loss: 3.1728
Iteration: 1373; Percent complete: 34.3%; Average loss: 3.4834
Iteration: 1374; Percent complete: 34.4%; Average loss: 3.3603
Iteration: 1375; Percent complete: 34.4%; Average loss: 3.2930
Iteration: 1376; Percent complete: 34.4%; Average loss: 3.2896
Iteration: 1377; Percent complete: 34.4%; Average loss: 3.4381
Iteration: 1378; Percent complete: 34.4%; Average loss: 3.5895
Iteration: 1379; Percent complete: 34.5%; Average loss: 3.4831
Iteration: 1380; Percent complete: 34.5%; Average loss: 3.2138
Iteration: 1381; Percent complete: 34.5%; Average loss: 3.5694
Iteration: 1382; Percent complete: 34.5%; Average loss: 3.2683
Iteration: 1383; Percent complete: 34.6%; Average loss: 3.2075
Iteration: 1384; Percent complete: 34.6%; Average loss: 3.2453
Iteration: 1385; Percent complete: 34.6%; Average loss: 3.4183
Iteration: 1386; Percent complete: 34.6%; Average loss: 3.2485
Iteration: 1387; Percent complete: 34.7%; Average loss: 3.4869
Iteration: 1388; Percent complete: 34.7%; Average loss: 3.2563
Iteration: 1389; Percent complete: 34.7%; Average loss: 3.1198
Iteration: 1390; Percent complete: 34.8%; Average loss: 3.1665
Iteration: 1391; Percent complete: 34.8%; Average loss: 3.1694
Iteration: 1392; Percent complete: 34.8%; Average loss: 3.4680
Iteration: 1393; Percent complete: 34.8%; Average loss: 3.2897
Iteration: 1394; Percent complete: 34.8%; Average loss: 3.2607
Iteration: 1395; Percent complete: 34.9%; Average loss: 3.3294
Iteration: 1396; Percent complete: 34.9%; Average loss: 3.4015
Iteration: 1397; Percent complete: 34.9%; Average loss: 3.3718
Iteration: 1398; Percent complete: 34.9%; Average loss: 3.3751
Iteration: 1399; Percent complete: 35.0%; Average loss: 3.4702
Iteration: 1400; Percent complete: 35.0%; Average loss: 3.4400
Iteration: 1401; Percent complete: 35.0%; Average loss: 3.5018
Iteration: 1402; Percent complete: 35.0%; Average loss: 3.2214
Iteration: 1403; Percent complete: 35.1%; Average loss: 3.4710
Iteration: 1404; Percent complete: 35.1%; Average loss: 3.2518
Iteration: 1405; Percent complete: 35.1%; Average loss: 3.0646
Iteration: 1406; Percent complete: 35.1%; Average loss: 3.3910
Iteration: 1407; Percent complete: 35.2%; Average loss: 3.3744
Iteration: 1408; Percent complete: 35.2%; Average loss: 3.3511
Iteration: 1409; Percent complete: 35.2%; Average loss: 3.0084
Iteration: 1410; Percent complete: 35.2%; Average loss: 3.5056
Iteration: 1411; Percent complete: 35.3%; Average loss: 3.6090
Iteration: 1412; Percent complete: 35.3%; Average loss: 2.9608
Iteration: 1413; Percent complete: 35.3%; Average loss: 3.1944
Iteration: 1414; Percent complete: 35.4%; Average loss: 3.1468
Iteration: 1415; Percent complete: 35.4%; Average loss: 3.2211
Iteration: 1416; Percent complete: 35.4%; Average loss: 3.2648
Iteration: 1417; Percent complete: 35.4%; Average loss: 3.5659
Iteration: 1418; Percent complete: 35.4%; Average loss: 3.4135
Iteration: 1419; Percent complete: 35.5%; Average loss: 3.3411
Iteration: 1420; Percent complete: 35.5%; Average loss: 3.2456
Iteration: 1421; Percent complete: 35.5%; Average loss: 3.4463
Iteration: 1422; Percent complete: 35.5%; Average loss: 3.4892
Iteration: 1423; Percent complete: 35.6%; Average loss: 2.9080
Iteration: 1424; Percent complete: 35.6%; Average loss: 3.1870
Iteration: 1425; Percent complete: 35.6%; Average loss: 3.2551
Iteration: 1426; Percent complete: 35.6%; Average loss: 3.4634
Iteration: 1427; Percent complete: 35.7%; Average loss: 3.2666
Iteration: 1428; Percent complete: 35.7%; Average loss: 3.3981
Iteration: 1429; Percent complete: 35.7%; Average loss: 3.3669
Iteration: 1430; Percent complete: 35.8%; Average loss: 3.6258
Iteration: 1431; Percent complete: 35.8%; Average loss: 3.5234
Iteration: 1432; Percent complete: 35.8%; Average loss: 2.9766
Iteration: 1433; Percent complete: 35.8%; Average loss: 3.2572
Iteration: 1434; Percent complete: 35.9%; Average loss: 3.3957
Iteration: 1435; Percent complete: 35.9%; Average loss: 3.2047
Iteration: 1436; Percent complete: 35.9%; Average loss: 3.3826
Iteration: 1437; Percent complete: 35.9%; Average loss: 3.3558
Iteration: 1438; Percent complete: 35.9%; Average loss: 3.4913
Iteration: 1439; Percent complete: 36.0%; Average loss: 3.3644
Iteration: 1440; Percent complete: 36.0%; Average loss: 2.9263
Iteration: 1441; Percent complete: 36.0%; Average loss: 3.3003
Iteration: 1442; Percent complete: 36.0%; Average loss: 3.4567
Iteration: 1443; Percent complete: 36.1%; Average loss: 3.2637
Iteration: 1444; Percent complete: 36.1%; Average loss: 3.3276
Iteration: 1445; Percent complete: 36.1%; Average loss: 3.4777
Iteration: 1446; Percent complete: 36.1%; Average loss: 3.2017
Iteration: 1447; Percent complete: 36.2%; Average loss: 3.3076
Iteration: 1448; Percent complete: 36.2%; Average loss: 3.3110
Iteration: 1449; Percent complete: 36.2%; Average loss: 3.3172
Iteration: 1450; Percent complete: 36.2%; Average loss: 3.1336
Iteration: 1451; Percent complete: 36.3%; Average loss: 3.3683
Iteration: 1452; Percent complete: 36.3%; Average loss: 3.2261
Iteration: 1453; Percent complete: 36.3%; Average loss: 3.2145
Iteration: 1454; Percent complete: 36.4%; Average loss: 3.2823
Iteration: 1455; Percent complete: 36.4%; Average loss: 3.3291
Iteration: 1456; Percent complete: 36.4%; Average loss: 3.2081
Iteration: 1457; Percent complete: 36.4%; Average loss: 3.2149
Iteration: 1458; Percent complete: 36.4%; Average loss: 3.1167
Iteration: 1459; Percent complete: 36.5%; Average loss: 3.4376
Iteration: 1460; Percent complete: 36.5%; Average loss: 3.4882
Iteration: 1461; Percent complete: 36.5%; Average loss: 3.5570
Iteration: 1462; Percent complete: 36.5%; Average loss: 3.1775
Iteration: 1463; Percent complete: 36.6%; Average loss: 3.4329
Iteration: 1464; Percent complete: 36.6%; Average loss: 3.2706
Iteration: 1465; Percent complete: 36.6%; Average loss: 3.0685
Iteration: 1466; Percent complete: 36.6%; Average loss: 3.1187
Iteration: 1467; Percent complete: 36.7%; Average loss: 3.2649
Iteration: 1468; Percent complete: 36.7%; Average loss: 3.1390
Iteration: 1469; Percent complete: 36.7%; Average loss: 3.4630
Iteration: 1470; Percent complete: 36.8%; Average loss: 3.4162
Iteration: 1471; Percent complete: 36.8%; Average loss: 3.3467
Iteration: 1472; Percent complete: 36.8%; Average loss: 3.5746
Iteration: 1473; Percent complete: 36.8%; Average loss: 3.2743
Iteration: 1474; Percent complete: 36.9%; Average loss: 3.5047
Iteration: 1475; Percent complete: 36.9%; Average loss: 3.1936
Iteration: 1476; Percent complete: 36.9%; Average loss: 3.2836
Iteration: 1477; Percent complete: 36.9%; Average loss: 3.3603
Iteration: 1478; Percent complete: 37.0%; Average loss: 3.3299
Iteration: 1479; Percent complete: 37.0%; Average loss: 3.3078
Iteration: 1480; Percent complete: 37.0%; Average loss: 3.1466
Iteration: 1481; Percent complete: 37.0%; Average loss: 3.5382
Iteration: 1482; Percent complete: 37.0%; Average loss: 3.4896
Iteration: 1483; Percent complete: 37.1%; Average loss: 3.1691
Iteration: 1484; Percent complete: 37.1%; Average loss: 3.4391
Iteration: 1485; Percent complete: 37.1%; Average loss: 3.3167
Iteration: 1486; Percent complete: 37.1%; Average loss: 3.2884
Iteration: 1487; Percent complete: 37.2%; Average loss: 3.2202
Iteration: 1488; Percent complete: 37.2%; Average loss: 3.1904
Iteration: 1489; Percent complete: 37.2%; Average loss: 3.6484
Iteration: 1490; Percent complete: 37.2%; Average loss: 2.8696
Iteration: 1491; Percent complete: 37.3%; Average loss: 3.3221
Iteration: 1492; Percent complete: 37.3%; Average loss: 3.4525
Iteration: 1493; Percent complete: 37.3%; Average loss: 3.2726
Iteration: 1494; Percent complete: 37.4%; Average loss: 3.2076
Iteration: 1495; Percent complete: 37.4%; Average loss: 3.3352
Iteration: 1496; Percent complete: 37.4%; Average loss: 3.2449
Iteration: 1497; Percent complete: 37.4%; Average loss: 3.0791
Iteration: 1498; Percent complete: 37.5%; Average loss: 3.2434
Iteration: 1499; Percent complete: 37.5%; Average loss: 3.4223
Iteration: 1500; Percent complete: 37.5%; Average loss: 3.4111
Iteration: 1501; Percent complete: 37.5%; Average loss: 3.1237
Iteration: 1502; Percent complete: 37.5%; Average loss: 3.6840
Iteration: 1503; Percent complete: 37.6%; Average loss: 3.2693
Iteration: 1504; Percent complete: 37.6%; Average loss: 3.3590
Iteration: 1505; Percent complete: 37.6%; Average loss: 3.0911
Iteration: 1506; Percent complete: 37.6%; Average loss: 3.2532
Iteration: 1507; Percent complete: 37.7%; Average loss: 3.2695
Iteration: 1508; Percent complete: 37.7%; Average loss: 3.0802
Iteration: 1509; Percent complete: 37.7%; Average loss: 3.3464
Iteration: 1510; Percent complete: 37.8%; Average loss: 3.3915
Iteration: 1511; Percent complete: 37.8%; Average loss: 3.3242
Iteration: 1512; Percent complete: 37.8%; Average loss: 3.2382
Iteration: 1513; Percent complete: 37.8%; Average loss: 3.3072
Iteration: 1514; Percent complete: 37.9%; Average loss: 3.2269
Iteration: 1515; Percent complete: 37.9%; Average loss: 3.3033
Iteration: 1516; Percent complete: 37.9%; Average loss: 3.2789
Iteration: 1517; Percent complete: 37.9%; Average loss: 3.4747
Iteration: 1518; Percent complete: 38.0%; Average loss: 2.9091
Iteration: 1519; Percent complete: 38.0%; Average loss: 3.3293
Iteration: 1520; Percent complete: 38.0%; Average loss: 3.2934
Iteration: 1521; Percent complete: 38.0%; Average loss: 3.2583
Iteration: 1522; Percent complete: 38.0%; Average loss: 3.2159
Iteration: 1523; Percent complete: 38.1%; Average loss: 3.2316
Iteration: 1524; Percent complete: 38.1%; Average loss: 3.2243
Iteration: 1525; Percent complete: 38.1%; Average loss: 3.1415
Iteration: 1526; Percent complete: 38.1%; Average loss: 3.5715
Iteration: 1527; Percent complete: 38.2%; Average loss: 3.2808
Iteration: 1528; Percent complete: 38.2%; Average loss: 3.1845
Iteration: 1529; Percent complete: 38.2%; Average loss: 3.3220
Iteration: 1530; Percent complete: 38.2%; Average loss: 3.3819
Iteration: 1531; Percent complete: 38.3%; Average loss: 3.0978
Iteration: 1532; Percent complete: 38.3%; Average loss: 3.3444
Iteration: 1533; Percent complete: 38.3%; Average loss: 3.1243
Iteration: 1534; Percent complete: 38.4%; Average loss: 3.3388
Iteration: 1535; Percent complete: 38.4%; Average loss: 3.2148
Iteration: 1536; Percent complete: 38.4%; Average loss: 3.4609
Iteration: 1537; Percent complete: 38.4%; Average loss: 3.4572
Iteration: 1538; Percent complete: 38.5%; Average loss: 3.3645
Iteration: 1539; Percent complete: 38.5%; Average loss: 3.5609
Iteration: 1540; Percent complete: 38.5%; Average loss: 3.3915
Iteration: 1541; Percent complete: 38.5%; Average loss: 3.0275
Iteration: 1542; Percent complete: 38.6%; Average loss: 3.2807
Iteration: 1543; Percent complete: 38.6%; Average loss: 2.9857
Iteration: 1544; Percent complete: 38.6%; Average loss: 3.2819
Iteration: 1545; Percent complete: 38.6%; Average loss: 3.3949
Iteration: 1546; Percent complete: 38.6%; Average loss: 3.3111
Iteration: 1547; Percent complete: 38.7%; Average loss: 3.4554
Iteration: 1548; Percent complete: 38.7%; Average loss: 2.9974
Iteration: 1549; Percent complete: 38.7%; Average loss: 3.2028
Iteration: 1550; Percent complete: 38.8%; Average loss: 3.1962
Iteration: 1551; Percent complete: 38.8%; Average loss: 3.4025
Iteration: 1552; Percent complete: 38.8%; Average loss: 3.3786
Iteration: 1553; Percent complete: 38.8%; Average loss: 3.0978
Iteration: 1554; Percent complete: 38.9%; Average loss: 3.4096
Iteration: 1555; Percent complete: 38.9%; Average loss: 3.1232
Iteration: 1556; Percent complete: 38.9%; Average loss: 3.4217
Iteration: 1557; Percent complete: 38.9%; Average loss: 3.2853
Iteration: 1558; Percent complete: 39.0%; Average loss: 3.1830
Iteration: 1559; Percent complete: 39.0%; Average loss: 3.2816
Iteration: 1560; Percent complete: 39.0%; Average loss: 3.4038
Iteration: 1561; Percent complete: 39.0%; Average loss: 3.2089
Iteration: 1562; Percent complete: 39.1%; Average loss: 3.4544
Iteration: 1563; Percent complete: 39.1%; Average loss: 3.0181
Iteration: 1564; Percent complete: 39.1%; Average loss: 3.3636
Iteration: 1565; Percent complete: 39.1%; Average loss: 3.0757
Iteration: 1566; Percent complete: 39.1%; Average loss: 3.0750
Iteration: 1567; Percent complete: 39.2%; Average loss: 3.3815
Iteration: 1568; Percent complete: 39.2%; Average loss: 3.2512
Iteration: 1569; Percent complete: 39.2%; Average loss: 3.6671
Iteration: 1570; Percent complete: 39.2%; Average loss: 3.3582
Iteration: 1571; Percent complete: 39.3%; Average loss: 3.2706
Iteration: 1572; Percent complete: 39.3%; Average loss: 3.2729
Iteration: 1573; Percent complete: 39.3%; Average loss: 3.3827
Iteration: 1574; Percent complete: 39.4%; Average loss: 3.1806
Iteration: 1575; Percent complete: 39.4%; Average loss: 3.2488
Iteration: 1576; Percent complete: 39.4%; Average loss: 3.2145
Iteration: 1577; Percent complete: 39.4%; Average loss: 3.2609
Iteration: 1578; Percent complete: 39.5%; Average loss: 3.4644
Iteration: 1579; Percent complete: 39.5%; Average loss: 3.3912
Iteration: 1580; Percent complete: 39.5%; Average loss: 3.3885
Iteration: 1581; Percent complete: 39.5%; Average loss: 3.2367
Iteration: 1582; Percent complete: 39.6%; Average loss: 3.4468
Iteration: 1583; Percent complete: 39.6%; Average loss: 3.0889
Iteration: 1584; Percent complete: 39.6%; Average loss: 3.0197
Iteration: 1585; Percent complete: 39.6%; Average loss: 3.2404
Iteration: 1586; Percent complete: 39.6%; Average loss: 3.5013
Iteration: 1587; Percent complete: 39.7%; Average loss: 3.1731
Iteration: 1588; Percent complete: 39.7%; Average loss: 3.2371
Iteration: 1589; Percent complete: 39.7%; Average loss: 3.2792
Iteration: 1590; Percent complete: 39.8%; Average loss: 3.3358
Iteration: 1591; Percent complete: 39.8%; Average loss: 3.3271
Iteration: 1592; Percent complete: 39.8%; Average loss: 3.0596
Iteration: 1593; Percent complete: 39.8%; Average loss: 3.2056
Iteration: 1594; Percent complete: 39.9%; Average loss: 3.2509
Iteration: 1595; Percent complete: 39.9%; Average loss: 3.1607
Iteration: 1596; Percent complete: 39.9%; Average loss: 3.4752
Iteration: 1597; Percent complete: 39.9%; Average loss: 3.1404
Iteration: 1598; Percent complete: 40.0%; Average loss: 3.1826
Iteration: 1599; Percent complete: 40.0%; Average loss: 3.5264
Iteration: 1600; Percent complete: 40.0%; Average loss: 3.5329
Iteration: 1601; Percent complete: 40.0%; Average loss: 3.3377
Iteration: 1602; Percent complete: 40.1%; Average loss: 3.2456
Iteration: 1603; Percent complete: 40.1%; Average loss: 3.4711
Iteration: 1604; Percent complete: 40.1%; Average loss: 3.0397
Iteration: 1605; Percent complete: 40.1%; Average loss: 3.2779
Iteration: 1606; Percent complete: 40.2%; Average loss: 3.2698
Iteration: 1607; Percent complete: 40.2%; Average loss: 3.2701
Iteration: 1608; Percent complete: 40.2%; Average loss: 3.2392
Iteration: 1609; Percent complete: 40.2%; Average loss: 3.3342
Iteration: 1610; Percent complete: 40.2%; Average loss: 3.4197
Iteration: 1611; Percent complete: 40.3%; Average loss: 3.0060
Iteration: 1612; Percent complete: 40.3%; Average loss: 3.3533
Iteration: 1613; Percent complete: 40.3%; Average loss: 3.3750
Iteration: 1614; Percent complete: 40.4%; Average loss: 3.3752
Iteration: 1615; Percent complete: 40.4%; Average loss: 3.1621
Iteration: 1616; Percent complete: 40.4%; Average loss: 3.1418
Iteration: 1617; Percent complete: 40.4%; Average loss: 3.3810
Iteration: 1618; Percent complete: 40.5%; Average loss: 3.3895
Iteration: 1619; Percent complete: 40.5%; Average loss: 3.3501
Iteration: 1620; Percent complete: 40.5%; Average loss: 3.1231
Iteration: 1621; Percent complete: 40.5%; Average loss: 2.8891
Iteration: 1622; Percent complete: 40.6%; Average loss: 3.3041
Iteration: 1623; Percent complete: 40.6%; Average loss: 3.1058
Iteration: 1624; Percent complete: 40.6%; Average loss: 3.4268
Iteration: 1625; Percent complete: 40.6%; Average loss: 3.0971
Iteration: 1626; Percent complete: 40.6%; Average loss: 3.4330
Iteration: 1627; Percent complete: 40.7%; Average loss: 3.2817
Iteration: 1628; Percent complete: 40.7%; Average loss: 3.1377
Iteration: 1629; Percent complete: 40.7%; Average loss: 3.2632
Iteration: 1630; Percent complete: 40.8%; Average loss: 3.1770
Iteration: 1631; Percent complete: 40.8%; Average loss: 3.3941
Iteration: 1632; Percent complete: 40.8%; Average loss: 3.2041
Iteration: 1633; Percent complete: 40.8%; Average loss: 3.2407
Iteration: 1634; Percent complete: 40.8%; Average loss: 3.3231
Iteration: 1635; Percent complete: 40.9%; Average loss: 3.3235
Iteration: 1636; Percent complete: 40.9%; Average loss: 3.0106
Iteration: 1637; Percent complete: 40.9%; Average loss: 3.2223
Iteration: 1638; Percent complete: 40.9%; Average loss: 3.2580
Iteration: 1639; Percent complete: 41.0%; Average loss: 3.0990
Iteration: 1640; Percent complete: 41.0%; Average loss: 3.2491
Iteration: 1641; Percent complete: 41.0%; Average loss: 3.2345
Iteration: 1642; Percent complete: 41.0%; Average loss: 3.1864
Iteration: 1643; Percent complete: 41.1%; Average loss: 3.3950
Iteration: 1644; Percent complete: 41.1%; Average loss: 3.2208
Iteration: 1645; Percent complete: 41.1%; Average loss: 3.0693
Iteration: 1646; Percent complete: 41.1%; Average loss: 3.4348
Iteration: 1647; Percent complete: 41.2%; Average loss: 3.0461
Iteration: 1648; Percent complete: 41.2%; Average loss: 3.6100
Iteration: 1649; Percent complete: 41.2%; Average loss: 3.2853
Iteration: 1650; Percent complete: 41.2%; Average loss: 3.1794
Iteration: 1651; Percent complete: 41.3%; Average loss: 3.4641
Iteration: 1652; Percent complete: 41.3%; Average loss: 3.2965
Iteration: 1653; Percent complete: 41.3%; Average loss: 3.2120
Iteration: 1654; Percent complete: 41.3%; Average loss: 3.5803
Iteration: 1655; Percent complete: 41.4%; Average loss: 3.1467
Iteration: 1656; Percent complete: 41.4%; Average loss: 3.1202
Iteration: 1657; Percent complete: 41.4%; Average loss: 3.2982
Iteration: 1658; Percent complete: 41.4%; Average loss: 3.3689
Iteration: 1659; Percent complete: 41.5%; Average loss: 3.3295
Iteration: 1660; Percent complete: 41.5%; Average loss: 3.2489
Iteration: 1661; Percent complete: 41.5%; Average loss: 3.0327
Iteration: 1662; Percent complete: 41.5%; Average loss: 3.0125
Iteration: 1663; Percent complete: 41.6%; Average loss: 3.0241
Iteration: 1664; Percent complete: 41.6%; Average loss: 3.4389
Iteration: 1665; Percent complete: 41.6%; Average loss: 3.3062
Iteration: 1666; Percent complete: 41.6%; Average loss: 3.3034
Iteration: 1667; Percent complete: 41.7%; Average loss: 3.3683
Iteration: 1668; Percent complete: 41.7%; Average loss: 3.3113
Iteration: 1669; Percent complete: 41.7%; Average loss: 3.5871
Iteration: 1670; Percent complete: 41.8%; Average loss: 3.1021
Iteration: 1671; Percent complete: 41.8%; Average loss: 3.1157
Iteration: 1672; Percent complete: 41.8%; Average loss: 3.2887
Iteration: 1673; Percent complete: 41.8%; Average loss: 3.1032
Iteration: 1674; Percent complete: 41.9%; Average loss: 3.3993
Iteration: 1675; Percent complete: 41.9%; Average loss: 3.1024
Iteration: 1676; Percent complete: 41.9%; Average loss: 3.2082
Iteration: 1677; Percent complete: 41.9%; Average loss: 3.2002
Iteration: 1678; Percent complete: 41.9%; Average loss: 3.3269
Iteration: 1679; Percent complete: 42.0%; Average loss: 3.2856
Iteration: 1680; Percent complete: 42.0%; Average loss: 3.2431
Iteration: 1681; Percent complete: 42.0%; Average loss: 3.3495
Iteration: 1682; Percent complete: 42.0%; Average loss: 3.5682
Iteration: 1683; Percent complete: 42.1%; Average loss: 3.4339
Iteration: 1684; Percent complete: 42.1%; Average loss: 3.4233
Iteration: 1685; Percent complete: 42.1%; Average loss: 3.3460
Iteration: 1686; Percent complete: 42.1%; Average loss: 3.5679
Iteration: 1687; Percent complete: 42.2%; Average loss: 3.4799
Iteration: 1688; Percent complete: 42.2%; Average loss: 3.3822
Iteration: 1689; Percent complete: 42.2%; Average loss: 3.0510
Iteration: 1690; Percent complete: 42.2%; Average loss: 3.1384
Iteration: 1691; Percent complete: 42.3%; Average loss: 3.2455
Iteration: 1692; Percent complete: 42.3%; Average loss: 3.1235
Iteration: 1693; Percent complete: 42.3%; Average loss: 3.2731
Iteration: 1694; Percent complete: 42.4%; Average loss: 3.1903
Iteration: 1695; Percent complete: 42.4%; Average loss: 3.2282
Iteration: 1696; Percent complete: 42.4%; Average loss: 2.9371
Iteration: 1697; Percent complete: 42.4%; Average loss: 3.2633
Iteration: 1698; Percent complete: 42.4%; Average loss: 3.0303
Iteration: 1699; Percent complete: 42.5%; Average loss: 3.4320
Iteration: 1700; Percent complete: 42.5%; Average loss: 3.3810
Iteration: 1701; Percent complete: 42.5%; Average loss: 3.0226
Iteration: 1702; Percent complete: 42.5%; Average loss: 3.1457
Iteration: 1703; Percent complete: 42.6%; Average loss: 3.2060
Iteration: 1704; Percent complete: 42.6%; Average loss: 3.2000
Iteration: 1705; Percent complete: 42.6%; Average loss: 3.2603
Iteration: 1706; Percent complete: 42.6%; Average loss: 2.7824
Iteration: 1707; Percent complete: 42.7%; Average loss: 3.3535
Iteration: 1708; Percent complete: 42.7%; Average loss: 3.3982
Iteration: 1709; Percent complete: 42.7%; Average loss: 3.1667
Iteration: 1710; Percent complete: 42.8%; Average loss: 3.4814
Iteration: 1711; Percent complete: 42.8%; Average loss: 3.3218
Iteration: 1712; Percent complete: 42.8%; Average loss: 3.2056
Iteration: 1713; Percent complete: 42.8%; Average loss: 2.8571
Iteration: 1714; Percent complete: 42.9%; Average loss: 3.1541
Iteration: 1715; Percent complete: 42.9%; Average loss: 3.2164
Iteration: 1716; Percent complete: 42.9%; Average loss: 3.1710
Iteration: 1717; Percent complete: 42.9%; Average loss: 3.4400
Iteration: 1718; Percent complete: 43.0%; Average loss: 3.2198
Iteration: 1719; Percent complete: 43.0%; Average loss: 3.3683
Iteration: 1720; Percent complete: 43.0%; Average loss: 3.1913
Iteration: 1721; Percent complete: 43.0%; Average loss: 2.9409
Iteration: 1722; Percent complete: 43.0%; Average loss: 3.3498
Iteration: 1723; Percent complete: 43.1%; Average loss: 3.3532
Iteration: 1724; Percent complete: 43.1%; Average loss: 3.3600
Iteration: 1725; Percent complete: 43.1%; Average loss: 3.4770
Iteration: 1726; Percent complete: 43.1%; Average loss: 3.2476
Iteration: 1727; Percent complete: 43.2%; Average loss: 3.0336
Iteration: 1728; Percent complete: 43.2%; Average loss: 3.1161
Iteration: 1729; Percent complete: 43.2%; Average loss: 3.1349
Iteration: 1730; Percent complete: 43.2%; Average loss: 3.3385
Iteration: 1731; Percent complete: 43.3%; Average loss: 3.1453
Iteration: 1732; Percent complete: 43.3%; Average loss: 2.9769
Iteration: 1733; Percent complete: 43.3%; Average loss: 3.2062
Iteration: 1734; Percent complete: 43.4%; Average loss: 3.2506
Iteration: 1735; Percent complete: 43.4%; Average loss: 3.3474
Iteration: 1736; Percent complete: 43.4%; Average loss: 2.9832
Iteration: 1737; Percent complete: 43.4%; Average loss: 3.2113
Iteration: 1738; Percent complete: 43.5%; Average loss: 3.1546
Iteration: 1739; Percent complete: 43.5%; Average loss: 3.4099
Iteration: 1740; Percent complete: 43.5%; Average loss: 2.8456
Iteration: 1741; Percent complete: 43.5%; Average loss: 3.6079
Iteration: 1742; Percent complete: 43.5%; Average loss: 3.1517
Iteration: 1743; Percent complete: 43.6%; Average loss: 3.3657
Iteration: 1744; Percent complete: 43.6%; Average loss: 2.9812
Iteration: 1745; Percent complete: 43.6%; Average loss: 3.3816
Iteration: 1746; Percent complete: 43.6%; Average loss: 3.2209
Iteration: 1747; Percent complete: 43.7%; Average loss: 3.2394
Iteration: 1748; Percent complete: 43.7%; Average loss: 3.3331
Iteration: 1749; Percent complete: 43.7%; Average loss: 3.2131
Iteration: 1750; Percent complete: 43.8%; Average loss: 3.0689
Iteration: 1751; Percent complete: 43.8%; Average loss: 2.9859
Iteration: 1752; Percent complete: 43.8%; Average loss: 3.0309
Iteration: 1753; Percent complete: 43.8%; Average loss: 3.5147
Iteration: 1754; Percent complete: 43.9%; Average loss: 3.1837
Iteration: 1755; Percent complete: 43.9%; Average loss: 3.2310
Iteration: 1756; Percent complete: 43.9%; Average loss: 3.2006
Iteration: 1757; Percent complete: 43.9%; Average loss: 3.2513
Iteration: 1758; Percent complete: 44.0%; Average loss: 3.2656
Iteration: 1759; Percent complete: 44.0%; Average loss: 3.1615
Iteration: 1760; Percent complete: 44.0%; Average loss: 3.1177
Iteration: 1761; Percent complete: 44.0%; Average loss: 3.1010
Iteration: 1762; Percent complete: 44.0%; Average loss: 3.2876
Iteration: 1763; Percent complete: 44.1%; Average loss: 3.1636
Iteration: 1764; Percent complete: 44.1%; Average loss: 3.1920
Iteration: 1765; Percent complete: 44.1%; Average loss: 3.3405
Iteration: 1766; Percent complete: 44.1%; Average loss: 3.0699
Iteration: 1767; Percent complete: 44.2%; Average loss: 3.3067
Iteration: 1768; Percent complete: 44.2%; Average loss: 3.1020
Iteration: 1769; Percent complete: 44.2%; Average loss: 3.2062
Iteration: 1770; Percent complete: 44.2%; Average loss: 3.2378
Iteration: 1771; Percent complete: 44.3%; Average loss: 3.0590
Iteration: 1772; Percent complete: 44.3%; Average loss: 3.1599
Iteration: 1773; Percent complete: 44.3%; Average loss: 2.9717
Iteration: 1774; Percent complete: 44.4%; Average loss: 3.2264
Iteration: 1775; Percent complete: 44.4%; Average loss: 3.1850
Iteration: 1776; Percent complete: 44.4%; Average loss: 3.2611
Iteration: 1777; Percent complete: 44.4%; Average loss: 3.3501
Iteration: 1778; Percent complete: 44.5%; Average loss: 3.4362
Iteration: 1779; Percent complete: 44.5%; Average loss: 3.0955
Iteration: 1780; Percent complete: 44.5%; Average loss: 3.3944
Iteration: 1781; Percent complete: 44.5%; Average loss: 3.4338
Iteration: 1782; Percent complete: 44.5%; Average loss: 3.3271
Iteration: 1783; Percent complete: 44.6%; Average loss: 3.2487
Iteration: 1784; Percent complete: 44.6%; Average loss: 3.2344
Iteration: 1785; Percent complete: 44.6%; Average loss: 3.0591
Iteration: 1786; Percent complete: 44.6%; Average loss: 3.1763
Iteration: 1787; Percent complete: 44.7%; Average loss: 3.0530
Iteration: 1788; Percent complete: 44.7%; Average loss: 3.2263
Iteration: 1789; Percent complete: 44.7%; Average loss: 3.4426
Iteration: 1790; Percent complete: 44.8%; Average loss: 3.2321
Iteration: 1791; Percent complete: 44.8%; Average loss: 3.3765
Iteration: 1792; Percent complete: 44.8%; Average loss: 3.3284
Iteration: 1793; Percent complete: 44.8%; Average loss: 3.3841
Iteration: 1794; Percent complete: 44.9%; Average loss: 3.0176
Iteration: 1795; Percent complete: 44.9%; Average loss: 3.1315
Iteration: 1796; Percent complete: 44.9%; Average loss: 3.0471
Iteration: 1797; Percent complete: 44.9%; Average loss: 2.9852
Iteration: 1798; Percent complete: 45.0%; Average loss: 3.2244
Iteration: 1799; Percent complete: 45.0%; Average loss: 3.4267
Iteration: 1800; Percent complete: 45.0%; Average loss: 3.2550
Iteration: 1801; Percent complete: 45.0%; Average loss: 3.1520
Iteration: 1802; Percent complete: 45.1%; Average loss: 3.1531
Iteration: 1803; Percent complete: 45.1%; Average loss: 3.3259
Iteration: 1804; Percent complete: 45.1%; Average loss: 3.0995
Iteration: 1805; Percent complete: 45.1%; Average loss: 2.8826
Iteration: 1806; Percent complete: 45.1%; Average loss: 3.2695
Iteration: 1807; Percent complete: 45.2%; Average loss: 3.3285
Iteration: 1808; Percent complete: 45.2%; Average loss: 3.2314
Iteration: 1809; Percent complete: 45.2%; Average loss: 3.4568
Iteration: 1810; Percent complete: 45.2%; Average loss: 3.3456
Iteration: 1811; Percent complete: 45.3%; Average loss: 3.3254
Iteration: 1812; Percent complete: 45.3%; Average loss: 3.2800
Iteration: 1813; Percent complete: 45.3%; Average loss: 3.2770
Iteration: 1814; Percent complete: 45.4%; Average loss: 3.2553
Iteration: 1815; Percent complete: 45.4%; Average loss: 3.0903
Iteration: 1816; Percent complete: 45.4%; Average loss: 3.0534
Iteration: 1817; Percent complete: 45.4%; Average loss: 3.1963
Iteration: 1818; Percent complete: 45.5%; Average loss: 3.2075
Iteration: 1819; Percent complete: 45.5%; Average loss: 3.2141
Iteration: 1820; Percent complete: 45.5%; Average loss: 3.1098
Iteration: 1821; Percent complete: 45.5%; Average loss: 3.0471
Iteration: 1822; Percent complete: 45.6%; Average loss: 3.2532
Iteration: 1823; Percent complete: 45.6%; Average loss: 3.0935
Iteration: 1824; Percent complete: 45.6%; Average loss: 3.2336
Iteration: 1825; Percent complete: 45.6%; Average loss: 3.2717
Iteration: 1826; Percent complete: 45.6%; Average loss: 3.3597
Iteration: 1827; Percent complete: 45.7%; Average loss: 3.3188
Iteration: 1828; Percent complete: 45.7%; Average loss: 3.0033
Iteration: 1829; Percent complete: 45.7%; Average loss: 3.2350
Iteration: 1830; Percent complete: 45.8%; Average loss: 3.2928
Iteration: 1831; Percent complete: 45.8%; Average loss: 3.1517
Iteration: 1832; Percent complete: 45.8%; Average loss: 3.2613
Iteration: 1833; Percent complete: 45.8%; Average loss: 3.3103
Iteration: 1834; Percent complete: 45.9%; Average loss: 3.0921
Iteration: 1835; Percent complete: 45.9%; Average loss: 3.1980
Iteration: 1836; Percent complete: 45.9%; Average loss: 3.1445
Iteration: 1837; Percent complete: 45.9%; Average loss: 3.3675
Iteration: 1838; Percent complete: 46.0%; Average loss: 3.2525
Iteration: 1839; Percent complete: 46.0%; Average loss: 3.3414
Iteration: 1840; Percent complete: 46.0%; Average loss: 3.3126
Iteration: 1841; Percent complete: 46.0%; Average loss: 3.0679
Iteration: 1842; Percent complete: 46.1%; Average loss: 3.2145
Iteration: 1843; Percent complete: 46.1%; Average loss: 3.1947
Iteration: 1844; Percent complete: 46.1%; Average loss: 3.2727
Iteration: 1845; Percent complete: 46.1%; Average loss: 3.2686
Iteration: 1846; Percent complete: 46.2%; Average loss: 3.3200
Iteration: 1847; Percent complete: 46.2%; Average loss: 3.1204
Iteration: 1848; Percent complete: 46.2%; Average loss: 3.2430
Iteration: 1849; Percent complete: 46.2%; Average loss: 3.1937
Iteration: 1850; Percent complete: 46.2%; Average loss: 2.9975
Iteration: 1851; Percent complete: 46.3%; Average loss: 3.1859
Iteration: 1852; Percent complete: 46.3%; Average loss: 3.2472
Iteration: 1853; Percent complete: 46.3%; Average loss: 3.1858
Iteration: 1854; Percent complete: 46.4%; Average loss: 3.3246
Iteration: 1855; Percent complete: 46.4%; Average loss: 3.1468
Iteration: 1856; Percent complete: 46.4%; Average loss: 3.2608
Iteration: 1857; Percent complete: 46.4%; Average loss: 3.1031
Iteration: 1858; Percent complete: 46.5%; Average loss: 3.3134
Iteration: 1859; Percent complete: 46.5%; Average loss: 3.3095
Iteration: 1860; Percent complete: 46.5%; Average loss: 3.0333
Iteration: 1861; Percent complete: 46.5%; Average loss: 3.2515
Iteration: 1862; Percent complete: 46.6%; Average loss: 3.5872
Iteration: 1863; Percent complete: 46.6%; Average loss: 3.3574
Iteration: 1864; Percent complete: 46.6%; Average loss: 3.2499
Iteration: 1865; Percent complete: 46.6%; Average loss: 3.1452
Iteration: 1866; Percent complete: 46.7%; Average loss: 3.1526
Iteration: 1867; Percent complete: 46.7%; Average loss: 2.9802
Iteration: 1868; Percent complete: 46.7%; Average loss: 3.4535
Iteration: 1869; Percent complete: 46.7%; Average loss: 3.2485
Iteration: 1870; Percent complete: 46.8%; Average loss: 3.0453
Iteration: 1871; Percent complete: 46.8%; Average loss: 3.2220
Iteration: 1872; Percent complete: 46.8%; Average loss: 2.8700
Iteration: 1873; Percent complete: 46.8%; Average loss: 3.1597
Iteration: 1874; Percent complete: 46.9%; Average loss: 2.9991
Iteration: 1875; Percent complete: 46.9%; Average loss: 3.3368
Iteration: 1876; Percent complete: 46.9%; Average loss: 3.2903
Iteration: 1877; Percent complete: 46.9%; Average loss: 3.4060
Iteration: 1878; Percent complete: 46.9%; Average loss: 3.6000
Iteration: 1879; Percent complete: 47.0%; Average loss: 3.1764
Iteration: 1880; Percent complete: 47.0%; Average loss: 3.4789
Iteration: 1881; Percent complete: 47.0%; Average loss: 2.9734
Iteration: 1882; Percent complete: 47.0%; Average loss: 3.2118
Iteration: 1883; Percent complete: 47.1%; Average loss: 3.1189
Iteration: 1884; Percent complete: 47.1%; Average loss: 2.9813
Iteration: 1885; Percent complete: 47.1%; Average loss: 3.1751
Iteration: 1886; Percent complete: 47.1%; Average loss: 2.9671
Iteration: 1887; Percent complete: 47.2%; Average loss: 3.1965
Iteration: 1888; Percent complete: 47.2%; Average loss: 3.0214
Iteration: 1889; Percent complete: 47.2%; Average loss: 3.3870
Iteration: 1890; Percent complete: 47.2%; Average loss: 3.1749
Iteration: 1891; Percent complete: 47.3%; Average loss: 3.1863
Iteration: 1892; Percent complete: 47.3%; Average loss: 3.3236
Iteration: 1893; Percent complete: 47.3%; Average loss: 3.2840
Iteration: 1894; Percent complete: 47.3%; Average loss: 3.0227
Iteration: 1895; Percent complete: 47.4%; Average loss: 2.9103
Iteration: 1896; Percent complete: 47.4%; Average loss: 3.0692
Iteration: 1897; Percent complete: 47.4%; Average loss: 3.1444
Iteration: 1898; Percent complete: 47.4%; Average loss: 3.1545
Iteration: 1899; Percent complete: 47.5%; Average loss: 2.9636
Iteration: 1900; Percent complete: 47.5%; Average loss: 3.0361
Iteration: 1901; Percent complete: 47.5%; Average loss: 3.2850
Iteration: 1902; Percent complete: 47.5%; Average loss: 3.0642
Iteration: 1903; Percent complete: 47.6%; Average loss: 3.3087
Iteration: 1904; Percent complete: 47.6%; Average loss: 3.1599
Iteration: 1905; Percent complete: 47.6%; Average loss: 3.4827
Iteration: 1906; Percent complete: 47.6%; Average loss: 3.1315
Iteration: 1907; Percent complete: 47.7%; Average loss: 3.0914
Iteration: 1908; Percent complete: 47.7%; Average loss: 3.6031
Iteration: 1909; Percent complete: 47.7%; Average loss: 3.0550
Iteration: 1910; Percent complete: 47.8%; Average loss: 3.4533
Iteration: 1911; Percent complete: 47.8%; Average loss: 3.0069
Iteration: 1912; Percent complete: 47.8%; Average loss: 3.2190
Iteration: 1913; Percent complete: 47.8%; Average loss: 3.2426
Iteration: 1914; Percent complete: 47.9%; Average loss: 3.0524
Iteration: 1915; Percent complete: 47.9%; Average loss: 2.8051
Iteration: 1916; Percent complete: 47.9%; Average loss: 3.2920
Iteration: 1917; Percent complete: 47.9%; Average loss: 3.3585
Iteration: 1918; Percent complete: 47.9%; Average loss: 3.1639
Iteration: 1919; Percent complete: 48.0%; Average loss: 3.0696
Iteration: 1920; Percent complete: 48.0%; Average loss: 2.9598
Iteration: 1921; Percent complete: 48.0%; Average loss: 3.2333
Iteration: 1922; Percent complete: 48.0%; Average loss: 3.1680
Iteration: 1923; Percent complete: 48.1%; Average loss: 3.0676
Iteration: 1924; Percent complete: 48.1%; Average loss: 3.1488
Iteration: 1925; Percent complete: 48.1%; Average loss: 3.1305
Iteration: 1926; Percent complete: 48.1%; Average loss: 3.0145
Iteration: 1927; Percent complete: 48.2%; Average loss: 2.8608
Iteration: 1928; Percent complete: 48.2%; Average loss: 3.2983
Iteration: 1929; Percent complete: 48.2%; Average loss: 3.3887
Iteration: 1930; Percent complete: 48.2%; Average loss: 3.2917
Iteration: 1931; Percent complete: 48.3%; Average loss: 3.0069
Iteration: 1932; Percent complete: 48.3%; Average loss: 3.2910
Iteration: 1933; Percent complete: 48.3%; Average loss: 3.2493
Iteration: 1934; Percent complete: 48.4%; Average loss: 3.0511
Iteration: 1935; Percent complete: 48.4%; Average loss: 3.4917
Iteration: 1936; Percent complete: 48.4%; Average loss: 3.0833
Iteration: 1937; Percent complete: 48.4%; Average loss: 3.0209
Iteration: 1938; Percent complete: 48.4%; Average loss: 3.1874
Iteration: 1939; Percent complete: 48.5%; Average loss: 3.0303
Iteration: 1940; Percent complete: 48.5%; Average loss: 3.1713
Iteration: 1941; Percent complete: 48.5%; Average loss: 3.0780
Iteration: 1942; Percent complete: 48.5%; Average loss: 3.2292
Iteration: 1943; Percent complete: 48.6%; Average loss: 3.2870
Iteration: 1944; Percent complete: 48.6%; Average loss: 3.2013
Iteration: 1945; Percent complete: 48.6%; Average loss: 3.2595
Iteration: 1946; Percent complete: 48.6%; Average loss: 3.3026
Iteration: 1947; Percent complete: 48.7%; Average loss: 3.3096
Iteration: 1948; Percent complete: 48.7%; Average loss: 3.3780
Iteration: 1949; Percent complete: 48.7%; Average loss: 3.1441
Iteration: 1950; Percent complete: 48.8%; Average loss: 3.1696
Iteration: 1951; Percent complete: 48.8%; Average loss: 3.2112
Iteration: 1952; Percent complete: 48.8%; Average loss: 3.0818
Iteration: 1953; Percent complete: 48.8%; Average loss: 3.4028
Iteration: 1954; Percent complete: 48.9%; Average loss: 2.9809
Iteration: 1955; Percent complete: 48.9%; Average loss: 3.1639
Iteration: 1956; Percent complete: 48.9%; Average loss: 2.8480
Iteration: 1957; Percent complete: 48.9%; Average loss: 2.9596
Iteration: 1958; Percent complete: 48.9%; Average loss: 3.1599
Iteration: 1959; Percent complete: 49.0%; Average loss: 3.2858
Iteration: 1960; Percent complete: 49.0%; Average loss: 2.9758
Iteration: 1961; Percent complete: 49.0%; Average loss: 3.4826
Iteration: 1962; Percent complete: 49.0%; Average loss: 3.5484
Iteration: 1963; Percent complete: 49.1%; Average loss: 3.2841
Iteration: 1964; Percent complete: 49.1%; Average loss: 2.9586
Iteration: 1965; Percent complete: 49.1%; Average loss: 2.9797
Iteration: 1966; Percent complete: 49.1%; Average loss: 3.1855
Iteration: 1967; Percent complete: 49.2%; Average loss: 3.1205
Iteration: 1968; Percent complete: 49.2%; Average loss: 3.1661
Iteration: 1969; Percent complete: 49.2%; Average loss: 3.0100
Iteration: 1970; Percent complete: 49.2%; Average loss: 3.2392
Iteration: 1971; Percent complete: 49.3%; Average loss: 3.3318
Iteration: 1972; Percent complete: 49.3%; Average loss: 3.2444
Iteration: 1973; Percent complete: 49.3%; Average loss: 2.8682
Iteration: 1974; Percent complete: 49.4%; Average loss: 2.9540
Iteration: 1975; Percent complete: 49.4%; Average loss: 3.4478
Iteration: 1976; Percent complete: 49.4%; Average loss: 2.8818
Iteration: 1977; Percent complete: 49.4%; Average loss: 3.1868
Iteration: 1978; Percent complete: 49.5%; Average loss: 3.3096
Iteration: 1979; Percent complete: 49.5%; Average loss: 3.1631
Iteration: 1980; Percent complete: 49.5%; Average loss: 3.1610
Iteration: 1981; Percent complete: 49.5%; Average loss: 3.2295
Iteration: 1982; Percent complete: 49.5%; Average loss: 3.1048
Iteration: 1983; Percent complete: 49.6%; Average loss: 3.1319
Iteration: 1984; Percent complete: 49.6%; Average loss: 3.0840
Iteration: 1985; Percent complete: 49.6%; Average loss: 3.1574
Iteration: 1986; Percent complete: 49.6%; Average loss: 3.2095
Iteration: 1987; Percent complete: 49.7%; Average loss: 3.3498
Iteration: 1988; Percent complete: 49.7%; Average loss: 3.2356
Iteration: 1989; Percent complete: 49.7%; Average loss: 3.1618
Iteration: 1990; Percent complete: 49.8%; Average loss: 3.2059
Iteration: 1991; Percent complete: 49.8%; Average loss: 3.0762
Iteration: 1992; Percent complete: 49.8%; Average loss: 3.0740
Iteration: 1993; Percent complete: 49.8%; Average loss: 3.4095
Iteration: 1994; Percent complete: 49.9%; Average loss: 3.1745
Iteration: 1995; Percent complete: 49.9%; Average loss: 3.1993
Iteration: 1996; Percent complete: 49.9%; Average loss: 2.9701
Iteration: 1997; Percent complete: 49.9%; Average loss: 3.3575
Iteration: 1998; Percent complete: 50.0%; Average loss: 3.3381
Iteration: 1999; Percent complete: 50.0%; Average loss: 3.2102
Iteration: 2000; Percent complete: 50.0%; Average loss: 2.8525
Iteration: 2001; Percent complete: 50.0%; Average loss: 3.2254
Iteration: 2002; Percent complete: 50.0%; Average loss: 2.9840
Iteration: 2003; Percent complete: 50.1%; Average loss: 3.0770
Iteration: 2004; Percent complete: 50.1%; Average loss: 3.1377
Iteration: 2005; Percent complete: 50.1%; Average loss: 3.1311
Iteration: 2006; Percent complete: 50.1%; Average loss: 3.0793
Iteration: 2007; Percent complete: 50.2%; Average loss: 3.1793
Iteration: 2008; Percent complete: 50.2%; Average loss: 3.1214
Iteration: 2009; Percent complete: 50.2%; Average loss: 3.2254
Iteration: 2010; Percent complete: 50.2%; Average loss: 3.1363
Iteration: 2011; Percent complete: 50.3%; Average loss: 3.1447
Iteration: 2012; Percent complete: 50.3%; Average loss: 2.9971
Iteration: 2013; Percent complete: 50.3%; Average loss: 3.2118
Iteration: 2014; Percent complete: 50.3%; Average loss: 3.1603
Iteration: 2015; Percent complete: 50.4%; Average loss: 3.3148
Iteration: 2016; Percent complete: 50.4%; Average loss: 3.1090
Iteration: 2017; Percent complete: 50.4%; Average loss: 3.0302
Iteration: 2018; Percent complete: 50.4%; Average loss: 2.9402
Iteration: 2019; Percent complete: 50.5%; Average loss: 3.2482
Iteration: 2020; Percent complete: 50.5%; Average loss: 3.0160
Iteration: 2021; Percent complete: 50.5%; Average loss: 2.9203
Iteration: 2022; Percent complete: 50.5%; Average loss: 2.9443
Iteration: 2023; Percent complete: 50.6%; Average loss: 3.0780
Iteration: 2024; Percent complete: 50.6%; Average loss: 3.3037
Iteration: 2025; Percent complete: 50.6%; Average loss: 3.2251
Iteration: 2026; Percent complete: 50.6%; Average loss: 3.1843
Iteration: 2027; Percent complete: 50.7%; Average loss: 2.8884
Iteration: 2028; Percent complete: 50.7%; Average loss: 3.0766
Iteration: 2029; Percent complete: 50.7%; Average loss: 3.1273
Iteration: 2030; Percent complete: 50.7%; Average loss: 3.2577
Iteration: 2031; Percent complete: 50.8%; Average loss: 2.9666
Iteration: 2032; Percent complete: 50.8%; Average loss: 3.5565
Iteration: 2033; Percent complete: 50.8%; Average loss: 3.4079
Iteration: 2034; Percent complete: 50.8%; Average loss: 3.5289
Iteration: 2035; Percent complete: 50.9%; Average loss: 3.1700
Iteration: 2036; Percent complete: 50.9%; Average loss: 3.1465
Iteration: 2037; Percent complete: 50.9%; Average loss: 3.4255
Iteration: 2038; Percent complete: 50.9%; Average loss: 3.1299
Iteration: 2039; Percent complete: 51.0%; Average loss: 3.2970
Iteration: 2040; Percent complete: 51.0%; Average loss: 3.3079
Iteration: 2041; Percent complete: 51.0%; Average loss: 3.2383
Iteration: 2042; Percent complete: 51.0%; Average loss: 3.1712
Iteration: 2043; Percent complete: 51.1%; Average loss: 2.9765
Iteration: 2044; Percent complete: 51.1%; Average loss: 3.1405
Iteration: 2045; Percent complete: 51.1%; Average loss: 3.3339
Iteration: 2046; Percent complete: 51.1%; Average loss: 3.1565
Iteration: 2047; Percent complete: 51.2%; Average loss: 3.1179
Iteration: 2048; Percent complete: 51.2%; Average loss: 3.1735
Iteration: 2049; Percent complete: 51.2%; Average loss: 2.9839
Iteration: 2050; Percent complete: 51.2%; Average loss: 3.1109
Iteration: 2051; Percent complete: 51.3%; Average loss: 3.0094
Iteration: 2052; Percent complete: 51.3%; Average loss: 2.8623
Iteration: 2053; Percent complete: 51.3%; Average loss: 2.9520
Iteration: 2054; Percent complete: 51.3%; Average loss: 3.1449
Iteration: 2055; Percent complete: 51.4%; Average loss: 2.9312
Iteration: 2056; Percent complete: 51.4%; Average loss: 3.1159
Iteration: 2057; Percent complete: 51.4%; Average loss: 3.0338
Iteration: 2058; Percent complete: 51.4%; Average loss: 2.9336
Iteration: 2059; Percent complete: 51.5%; Average loss: 3.2328
Iteration: 2060; Percent complete: 51.5%; Average loss: 3.0050
Iteration: 2061; Percent complete: 51.5%; Average loss: 3.0666
Iteration: 2062; Percent complete: 51.5%; Average loss: 3.1908
Iteration: 2063; Percent complete: 51.6%; Average loss: 3.3168
Iteration: 2064; Percent complete: 51.6%; Average loss: 2.8786
Iteration: 2065; Percent complete: 51.6%; Average loss: 3.0190
Iteration: 2066; Percent complete: 51.6%; Average loss: 3.0948
Iteration: 2067; Percent complete: 51.7%; Average loss: 3.0500
Iteration: 2068; Percent complete: 51.7%; Average loss: 3.2245
Iteration: 2069; Percent complete: 51.7%; Average loss: 3.2264
Iteration: 2070; Percent complete: 51.7%; Average loss: 3.0537
Iteration: 2071; Percent complete: 51.8%; Average loss: 3.4845
Iteration: 2072; Percent complete: 51.8%; Average loss: 3.2799
Iteration: 2073; Percent complete: 51.8%; Average loss: 3.1373
Iteration: 2074; Percent complete: 51.8%; Average loss: 3.3520
Iteration: 2075; Percent complete: 51.9%; Average loss: 3.0138
Iteration: 2076; Percent complete: 51.9%; Average loss: 3.1066
Iteration: 2077; Percent complete: 51.9%; Average loss: 3.1692
Iteration: 2078; Percent complete: 51.9%; Average loss: 2.7993
Iteration: 2079; Percent complete: 52.0%; Average loss: 3.1722
Iteration: 2080; Percent complete: 52.0%; Average loss: 3.0819
Iteration: 2081; Percent complete: 52.0%; Average loss: 3.2011
Iteration: 2082; Percent complete: 52.0%; Average loss: 3.1321
Iteration: 2083; Percent complete: 52.1%; Average loss: 3.1251
Iteration: 2084; Percent complete: 52.1%; Average loss: 3.2163
Iteration: 2085; Percent complete: 52.1%; Average loss: 3.4943
Iteration: 2086; Percent complete: 52.1%; Average loss: 3.3009
Iteration: 2087; Percent complete: 52.2%; Average loss: 3.2050
Iteration: 2088; Percent complete: 52.2%; Average loss: 3.0660
Iteration: 2089; Percent complete: 52.2%; Average loss: 3.1325
Iteration: 2090; Percent complete: 52.2%; Average loss: 3.2161
Iteration: 2091; Percent complete: 52.3%; Average loss: 2.9936
Iteration: 2092; Percent complete: 52.3%; Average loss: 3.0793
Iteration: 2093; Percent complete: 52.3%; Average loss: 3.0666
Iteration: 2094; Percent complete: 52.3%; Average loss: 3.2706
Iteration: 2095; Percent complete: 52.4%; Average loss: 2.9900
Iteration: 2096; Percent complete: 52.4%; Average loss: 3.3356
Iteration: 2097; Percent complete: 52.4%; Average loss: 3.1394
Iteration: 2098; Percent complete: 52.4%; Average loss: 3.0880
Iteration: 2099; Percent complete: 52.5%; Average loss: 3.0411
Iteration: 2100; Percent complete: 52.5%; Average loss: 3.1848
Iteration: 2101; Percent complete: 52.5%; Average loss: 3.4594
Iteration: 2102; Percent complete: 52.5%; Average loss: 3.1744
Iteration: 2103; Percent complete: 52.6%; Average loss: 3.2921
Iteration: 2104; Percent complete: 52.6%; Average loss: 3.1089
Iteration: 2105; Percent complete: 52.6%; Average loss: 2.9200
Iteration: 2106; Percent complete: 52.6%; Average loss: 3.3701
Iteration: 2107; Percent complete: 52.7%; Average loss: 2.6706
Iteration: 2108; Percent complete: 52.7%; Average loss: 3.0730
Iteration: 2109; Percent complete: 52.7%; Average loss: 3.1634
Iteration: 2110; Percent complete: 52.8%; Average loss: 3.1638
Iteration: 2111; Percent complete: 52.8%; Average loss: 3.1804
Iteration: 2112; Percent complete: 52.8%; Average loss: 3.0972
Iteration: 2113; Percent complete: 52.8%; Average loss: 3.2943
Iteration: 2114; Percent complete: 52.8%; Average loss: 3.2953
Iteration: 2115; Percent complete: 52.9%; Average loss: 3.3539
Iteration: 2116; Percent complete: 52.9%; Average loss: 3.2199
Iteration: 2117; Percent complete: 52.9%; Average loss: 3.0058
Iteration: 2118; Percent complete: 52.9%; Average loss: 2.9961
Iteration: 2119; Percent complete: 53.0%; Average loss: 3.1485
Iteration: 2120; Percent complete: 53.0%; Average loss: 2.9526
Iteration: 2121; Percent complete: 53.0%; Average loss: 3.3438
Iteration: 2122; Percent complete: 53.0%; Average loss: 3.2261
Iteration: 2123; Percent complete: 53.1%; Average loss: 2.9470
Iteration: 2124; Percent complete: 53.1%; Average loss: 3.1544
Iteration: 2125; Percent complete: 53.1%; Average loss: 3.0623
Iteration: 2126; Percent complete: 53.1%; Average loss: 2.7885
Iteration: 2127; Percent complete: 53.2%; Average loss: 3.0505
Iteration: 2128; Percent complete: 53.2%; Average loss: 3.1656
Iteration: 2129; Percent complete: 53.2%; Average loss: 3.2831
Iteration: 2130; Percent complete: 53.2%; Average loss: 2.9910
Iteration: 2131; Percent complete: 53.3%; Average loss: 3.2101
Iteration: 2132; Percent complete: 53.3%; Average loss: 2.9462
Iteration: 2133; Percent complete: 53.3%; Average loss: 3.0997
Iteration: 2134; Percent complete: 53.3%; Average loss: 3.3532
Iteration: 2135; Percent complete: 53.4%; Average loss: 3.0644
Iteration: 2136; Percent complete: 53.4%; Average loss: 3.1333
Iteration: 2137; Percent complete: 53.4%; Average loss: 3.2140
Iteration: 2138; Percent complete: 53.4%; Average loss: 3.4349
Iteration: 2139; Percent complete: 53.5%; Average loss: 2.9291
Iteration: 2140; Percent complete: 53.5%; Average loss: 3.1560
Iteration: 2141; Percent complete: 53.5%; Average loss: 3.3928
Iteration: 2142; Percent complete: 53.5%; Average loss: 3.2884
Iteration: 2143; Percent complete: 53.6%; Average loss: 3.2809
Iteration: 2144; Percent complete: 53.6%; Average loss: 3.0559
Iteration: 2145; Percent complete: 53.6%; Average loss: 3.1693
Iteration: 2146; Percent complete: 53.6%; Average loss: 3.1131
Iteration: 2147; Percent complete: 53.7%; Average loss: 3.6086
Iteration: 2148; Percent complete: 53.7%; Average loss: 3.2025
Iteration: 2149; Percent complete: 53.7%; Average loss: 3.0475
Iteration: 2150; Percent complete: 53.8%; Average loss: 3.3253
Iteration: 2151; Percent complete: 53.8%; Average loss: 3.0977
Iteration: 2152; Percent complete: 53.8%; Average loss: 3.0998
Iteration: 2153; Percent complete: 53.8%; Average loss: 3.1546
Iteration: 2154; Percent complete: 53.8%; Average loss: 2.9674
Iteration: 2155; Percent complete: 53.9%; Average loss: 3.0551
Iteration: 2156; Percent complete: 53.9%; Average loss: 3.1947
Iteration: 2157; Percent complete: 53.9%; Average loss: 3.0252
Iteration: 2158; Percent complete: 53.9%; Average loss: 3.1219
Iteration: 2159; Percent complete: 54.0%; Average loss: 3.0138
Iteration: 2160; Percent complete: 54.0%; Average loss: 3.2519
Iteration: 2161; Percent complete: 54.0%; Average loss: 2.8227
Iteration: 2162; Percent complete: 54.0%; Average loss: 3.2086
Iteration: 2163; Percent complete: 54.1%; Average loss: 3.1891
Iteration: 2164; Percent complete: 54.1%; Average loss: 3.2058
Iteration: 2165; Percent complete: 54.1%; Average loss: 2.9873
Iteration: 2166; Percent complete: 54.1%; Average loss: 3.3314
Iteration: 2167; Percent complete: 54.2%; Average loss: 3.1207
Iteration: 2168; Percent complete: 54.2%; Average loss: 3.2461
Iteration: 2169; Percent complete: 54.2%; Average loss: 2.8866
Iteration: 2170; Percent complete: 54.2%; Average loss: 2.8923
Iteration: 2171; Percent complete: 54.3%; Average loss: 3.0280
Iteration: 2172; Percent complete: 54.3%; Average loss: 3.1058
Iteration: 2173; Percent complete: 54.3%; Average loss: 3.1790
Iteration: 2174; Percent complete: 54.4%; Average loss: 3.0108
Iteration: 2175; Percent complete: 54.4%; Average loss: 2.8398
Iteration: 2176; Percent complete: 54.4%; Average loss: 3.1197
Iteration: 2177; Percent complete: 54.4%; Average loss: 3.2544
Iteration: 2178; Percent complete: 54.4%; Average loss: 3.0495
Iteration: 2179; Percent complete: 54.5%; Average loss: 3.0378
Iteration: 2180; Percent complete: 54.5%; Average loss: 2.9640
Iteration: 2181; Percent complete: 54.5%; Average loss: 2.9719
Iteration: 2182; Percent complete: 54.5%; Average loss: 3.3234
Iteration: 2183; Percent complete: 54.6%; Average loss: 3.2174
Iteration: 2184; Percent complete: 54.6%; Average loss: 3.3656
Iteration: 2185; Percent complete: 54.6%; Average loss: 3.1984
Iteration: 2186; Percent complete: 54.6%; Average loss: 3.1346
Iteration: 2187; Percent complete: 54.7%; Average loss: 3.2436
Iteration: 2188; Percent complete: 54.7%; Average loss: 2.9737
Iteration: 2189; Percent complete: 54.7%; Average loss: 3.0682
Iteration: 2190; Percent complete: 54.8%; Average loss: 3.1946
Iteration: 2191; Percent complete: 54.8%; Average loss: 3.1715
Iteration: 2192; Percent complete: 54.8%; Average loss: 3.0778
Iteration: 2193; Percent complete: 54.8%; Average loss: 3.0449
Iteration: 2194; Percent complete: 54.9%; Average loss: 3.0936
Iteration: 2195; Percent complete: 54.9%; Average loss: 3.0436
Iteration: 2196; Percent complete: 54.9%; Average loss: 3.3209
Iteration: 2197; Percent complete: 54.9%; Average loss: 2.9316
Iteration: 2198; Percent complete: 54.9%; Average loss: 3.2071
Iteration: 2199; Percent complete: 55.0%; Average loss: 3.3263
Iteration: 2200; Percent complete: 55.0%; Average loss: 3.2127
Iteration: 2201; Percent complete: 55.0%; Average loss: 2.7285
Iteration: 2202; Percent complete: 55.0%; Average loss: 3.0542
Iteration: 2203; Percent complete: 55.1%; Average loss: 2.8635
Iteration: 2204; Percent complete: 55.1%; Average loss: 3.2683
Iteration: 2205; Percent complete: 55.1%; Average loss: 3.0689
Iteration: 2206; Percent complete: 55.1%; Average loss: 3.3100
Iteration: 2207; Percent complete: 55.2%; Average loss: 3.2274
Iteration: 2208; Percent complete: 55.2%; Average loss: 3.3098
Iteration: 2209; Percent complete: 55.2%; Average loss: 3.0812
Iteration: 2210; Percent complete: 55.2%; Average loss: 3.1341
Iteration: 2211; Percent complete: 55.3%; Average loss: 3.2141
Iteration: 2212; Percent complete: 55.3%; Average loss: 3.1888
Iteration: 2213; Percent complete: 55.3%; Average loss: 3.2171
Iteration: 2214; Percent complete: 55.4%; Average loss: 3.0845
Iteration: 2215; Percent complete: 55.4%; Average loss: 3.1985
Iteration: 2216; Percent complete: 55.4%; Average loss: 3.2552
Iteration: 2217; Percent complete: 55.4%; Average loss: 2.9626
Iteration: 2218; Percent complete: 55.5%; Average loss: 3.0621
Iteration: 2219; Percent complete: 55.5%; Average loss: 3.0441
Iteration: 2220; Percent complete: 55.5%; Average loss: 2.8734
Iteration: 2221; Percent complete: 55.5%; Average loss: 3.1342
Iteration: 2222; Percent complete: 55.5%; Average loss: 3.1245
Iteration: 2223; Percent complete: 55.6%; Average loss: 2.9993
Iteration: 2224; Percent complete: 55.6%; Average loss: 2.9867
Iteration: 2225; Percent complete: 55.6%; Average loss: 3.1331
Iteration: 2226; Percent complete: 55.6%; Average loss: 2.8444
Iteration: 2227; Percent complete: 55.7%; Average loss: 3.2433
Iteration: 2228; Percent complete: 55.7%; Average loss: 2.8554
Iteration: 2229; Percent complete: 55.7%; Average loss: 3.2323
Iteration: 2230; Percent complete: 55.8%; Average loss: 3.1680
Iteration: 2231; Percent complete: 55.8%; Average loss: 3.0499
Iteration: 2232; Percent complete: 55.8%; Average loss: 3.0788
Iteration: 2233; Percent complete: 55.8%; Average loss: 2.9222
Iteration: 2234; Percent complete: 55.9%; Average loss: 2.8222
Iteration: 2235; Percent complete: 55.9%; Average loss: 3.1580
Iteration: 2236; Percent complete: 55.9%; Average loss: 3.1193
Iteration: 2237; Percent complete: 55.9%; Average loss: 3.3290
Iteration: 2238; Percent complete: 56.0%; Average loss: 3.0774
Iteration: 2239; Percent complete: 56.0%; Average loss: 3.2572
Iteration: 2240; Percent complete: 56.0%; Average loss: 3.2926
Iteration: 2241; Percent complete: 56.0%; Average loss: 3.2154
Iteration: 2242; Percent complete: 56.0%; Average loss: 3.1496
Iteration: 2243; Percent complete: 56.1%; Average loss: 3.0626
Iteration: 2244; Percent complete: 56.1%; Average loss: 3.0065
Iteration: 2245; Percent complete: 56.1%; Average loss: 2.9584
Iteration: 2246; Percent complete: 56.1%; Average loss: 3.0098
Iteration: 2247; Percent complete: 56.2%; Average loss: 3.3607
Iteration: 2248; Percent complete: 56.2%; Average loss: 3.0849
Iteration: 2249; Percent complete: 56.2%; Average loss: 3.2349
Iteration: 2250; Percent complete: 56.2%; Average loss: 3.0078
Iteration: 2251; Percent complete: 56.3%; Average loss: 3.1977
Iteration: 2252; Percent complete: 56.3%; Average loss: 2.9315
Iteration: 2253; Percent complete: 56.3%; Average loss: 3.1049
Iteration: 2254; Percent complete: 56.4%; Average loss: 3.1860
Iteration: 2255; Percent complete: 56.4%; Average loss: 3.1921
Iteration: 2256; Percent complete: 56.4%; Average loss: 3.1425
Iteration: 2257; Percent complete: 56.4%; Average loss: 3.0339
Iteration: 2258; Percent complete: 56.5%; Average loss: 2.9973
Iteration: 2259; Percent complete: 56.5%; Average loss: 3.2283
Iteration: 2260; Percent complete: 56.5%; Average loss: 3.0832
Iteration: 2261; Percent complete: 56.5%; Average loss: 3.1255
Iteration: 2262; Percent complete: 56.5%; Average loss: 3.0938
Iteration: 2263; Percent complete: 56.6%; Average loss: 3.0702
Iteration: 2264; Percent complete: 56.6%; Average loss: 2.8837
Iteration: 2265; Percent complete: 56.6%; Average loss: 3.2973
Iteration: 2266; Percent complete: 56.6%; Average loss: 3.0180
Iteration: 2267; Percent complete: 56.7%; Average loss: 3.1229
Iteration: 2268; Percent complete: 56.7%; Average loss: 2.8703
Iteration: 2269; Percent complete: 56.7%; Average loss: 3.2583
Iteration: 2270; Percent complete: 56.8%; Average loss: 2.9604
Iteration: 2271; Percent complete: 56.8%; Average loss: 3.0901
Iteration: 2272; Percent complete: 56.8%; Average loss: 3.2212
Iteration: 2273; Percent complete: 56.8%; Average loss: 2.9807
Iteration: 2274; Percent complete: 56.9%; Average loss: 3.1843
Iteration: 2275; Percent complete: 56.9%; Average loss: 3.2272
Iteration: 2276; Percent complete: 56.9%; Average loss: 2.9485
Iteration: 2277; Percent complete: 56.9%; Average loss: 3.0547
Iteration: 2278; Percent complete: 57.0%; Average loss: 3.3058
Iteration: 2279; Percent complete: 57.0%; Average loss: 3.0219
Iteration: 2280; Percent complete: 57.0%; Average loss: 3.3226
Iteration: 2281; Percent complete: 57.0%; Average loss: 2.9955
Iteration: 2282; Percent complete: 57.0%; Average loss: 3.0132
Iteration: 2283; Percent complete: 57.1%; Average loss: 2.9874
Iteration: 2284; Percent complete: 57.1%; Average loss: 3.2792
Iteration: 2285; Percent complete: 57.1%; Average loss: 3.1163
Iteration: 2286; Percent complete: 57.1%; Average loss: 3.0313
Iteration: 2287; Percent complete: 57.2%; Average loss: 2.8252
Iteration: 2288; Percent complete: 57.2%; Average loss: 2.9585
Iteration: 2289; Percent complete: 57.2%; Average loss: 3.0659
Iteration: 2290; Percent complete: 57.2%; Average loss: 3.1732
Iteration: 2291; Percent complete: 57.3%; Average loss: 3.1985
Iteration: 2292; Percent complete: 57.3%; Average loss: 3.0998
Iteration: 2293; Percent complete: 57.3%; Average loss: 3.0774
Iteration: 2294; Percent complete: 57.4%; Average loss: 3.1479
Iteration: 2295; Percent complete: 57.4%; Average loss: 2.9007
Iteration: 2296; Percent complete: 57.4%; Average loss: 3.2467
Iteration: 2297; Percent complete: 57.4%; Average loss: 2.8997
Iteration: 2298; Percent complete: 57.5%; Average loss: 3.0229
Iteration: 2299; Percent complete: 57.5%; Average loss: 3.2595
Iteration: 2300; Percent complete: 57.5%; Average loss: 3.0515
Iteration: 2301; Percent complete: 57.5%; Average loss: 3.0069
Iteration: 2302; Percent complete: 57.6%; Average loss: 2.8448
Iteration: 2303; Percent complete: 57.6%; Average loss: 3.0207
Iteration: 2304; Percent complete: 57.6%; Average loss: 3.0847
Iteration: 2305; Percent complete: 57.6%; Average loss: 3.2270
Iteration: 2306; Percent complete: 57.6%; Average loss: 3.1291
Iteration: 2307; Percent complete: 57.7%; Average loss: 2.8455
Iteration: 2308; Percent complete: 57.7%; Average loss: 3.4163
Iteration: 2309; Percent complete: 57.7%; Average loss: 3.1368
Iteration: 2310; Percent complete: 57.8%; Average loss: 3.0079
Iteration: 2311; Percent complete: 57.8%; Average loss: 3.1885
Iteration: 2312; Percent complete: 57.8%; Average loss: 2.9403
Iteration: 2313; Percent complete: 57.8%; Average loss: 2.8668
Iteration: 2314; Percent complete: 57.9%; Average loss: 3.1685
Iteration: 2315; Percent complete: 57.9%; Average loss: 3.0497
Iteration: 2316; Percent complete: 57.9%; Average loss: 2.9407
Iteration: 2317; Percent complete: 57.9%; Average loss: 2.8618
Iteration: 2318; Percent complete: 58.0%; Average loss: 2.9782
Iteration: 2319; Percent complete: 58.0%; Average loss: 2.8361
Iteration: 2320; Percent complete: 58.0%; Average loss: 2.8449
Iteration: 2321; Percent complete: 58.0%; Average loss: 3.1141
Iteration: 2322; Percent complete: 58.1%; Average loss: 2.9796
Iteration: 2323; Percent complete: 58.1%; Average loss: 3.2358
Iteration: 2324; Percent complete: 58.1%; Average loss: 3.0976
Iteration: 2325; Percent complete: 58.1%; Average loss: 2.8400
Iteration: 2326; Percent complete: 58.1%; Average loss: 3.1284
Iteration: 2327; Percent complete: 58.2%; Average loss: 2.8533
Iteration: 2328; Percent complete: 58.2%; Average loss: 2.9951
Iteration: 2329; Percent complete: 58.2%; Average loss: 3.0092
Iteration: 2330; Percent complete: 58.2%; Average loss: 3.0512
Iteration: 2331; Percent complete: 58.3%; Average loss: 3.0724
Iteration: 2332; Percent complete: 58.3%; Average loss: 2.9839
Iteration: 2333; Percent complete: 58.3%; Average loss: 3.3315
Iteration: 2334; Percent complete: 58.4%; Average loss: 3.1730
Iteration: 2335; Percent complete: 58.4%; Average loss: 2.7299
Iteration: 2336; Percent complete: 58.4%; Average loss: 2.9949
Iteration: 2337; Percent complete: 58.4%; Average loss: 3.0501
Iteration: 2338; Percent complete: 58.5%; Average loss: 2.8159
Iteration: 2339; Percent complete: 58.5%; Average loss: 3.1556
Iteration: 2340; Percent complete: 58.5%; Average loss: 2.9652
Iteration: 2341; Percent complete: 58.5%; Average loss: 3.0374
Iteration: 2342; Percent complete: 58.6%; Average loss: 3.1540
Iteration: 2343; Percent complete: 58.6%; Average loss: 3.1941
Iteration: 2344; Percent complete: 58.6%; Average loss: 2.8641
Iteration: 2345; Percent complete: 58.6%; Average loss: 3.0073
Iteration: 2346; Percent complete: 58.7%; Average loss: 2.9685
Iteration: 2347; Percent complete: 58.7%; Average loss: 3.1591
Iteration: 2348; Percent complete: 58.7%; Average loss: 2.9730
Iteration: 2349; Percent complete: 58.7%; Average loss: 3.0303
Iteration: 2350; Percent complete: 58.8%; Average loss: 3.2939
Iteration: 2351; Percent complete: 58.8%; Average loss: 2.8971
Iteration: 2352; Percent complete: 58.8%; Average loss: 2.9594
Iteration: 2353; Percent complete: 58.8%; Average loss: 3.2248
Iteration: 2354; Percent complete: 58.9%; Average loss: 2.9996
Iteration: 2355; Percent complete: 58.9%; Average loss: 3.2668
Iteration: 2356; Percent complete: 58.9%; Average loss: 3.0432
Iteration: 2357; Percent complete: 58.9%; Average loss: 2.6973
Iteration: 2358; Percent complete: 59.0%; Average loss: 3.1102
Iteration: 2359; Percent complete: 59.0%; Average loss: 3.1666
Iteration: 2360; Percent complete: 59.0%; Average loss: 3.0370
Iteration: 2361; Percent complete: 59.0%; Average loss: 3.1959
Iteration: 2362; Percent complete: 59.1%; Average loss: 3.0264
Iteration: 2363; Percent complete: 59.1%; Average loss: 3.1717
Iteration: 2364; Percent complete: 59.1%; Average loss: 3.1668
Iteration: 2365; Percent complete: 59.1%; Average loss: 2.7807
Iteration: 2366; Percent complete: 59.2%; Average loss: 3.1730
Iteration: 2367; Percent complete: 59.2%; Average loss: 2.8663
Iteration: 2368; Percent complete: 59.2%; Average loss: 3.0310
Iteration: 2369; Percent complete: 59.2%; Average loss: 3.1328
Iteration: 2370; Percent complete: 59.2%; Average loss: 3.2035
Iteration: 2371; Percent complete: 59.3%; Average loss: 3.1297
Iteration: 2372; Percent complete: 59.3%; Average loss: 3.0306
Iteration: 2373; Percent complete: 59.3%; Average loss: 2.7837
Iteration: 2374; Percent complete: 59.4%; Average loss: 3.0864
Iteration: 2375; Percent complete: 59.4%; Average loss: 2.9412
Iteration: 2376; Percent complete: 59.4%; Average loss: 3.1406
Iteration: 2377; Percent complete: 59.4%; Average loss: 2.9974
Iteration: 2378; Percent complete: 59.5%; Average loss: 2.7302
Iteration: 2379; Percent complete: 59.5%; Average loss: 3.2269
Iteration: 2380; Percent complete: 59.5%; Average loss: 3.1207
Iteration: 2381; Percent complete: 59.5%; Average loss: 2.9620
Iteration: 2382; Percent complete: 59.6%; Average loss: 3.0790
Iteration: 2383; Percent complete: 59.6%; Average loss: 3.1439
Iteration: 2384; Percent complete: 59.6%; Average loss: 3.0446
Iteration: 2385; Percent complete: 59.6%; Average loss: 3.1038
Iteration: 2386; Percent complete: 59.7%; Average loss: 3.0558
Iteration: 2387; Percent complete: 59.7%; Average loss: 2.8551
Iteration: 2388; Percent complete: 59.7%; Average loss: 3.1326
Iteration: 2389; Percent complete: 59.7%; Average loss: 2.9068
Iteration: 2390; Percent complete: 59.8%; Average loss: 2.9061
Iteration: 2391; Percent complete: 59.8%; Average loss: 2.9072
Iteration: 2392; Percent complete: 59.8%; Average loss: 3.0743
Iteration: 2393; Percent complete: 59.8%; Average loss: 2.9381
Iteration: 2394; Percent complete: 59.9%; Average loss: 3.0698
Iteration: 2395; Percent complete: 59.9%; Average loss: 3.1261
Iteration: 2396; Percent complete: 59.9%; Average loss: 3.0551
Iteration: 2397; Percent complete: 59.9%; Average loss: 2.8952
Iteration: 2398; Percent complete: 60.0%; Average loss: 3.2688
Iteration: 2399; Percent complete: 60.0%; Average loss: 3.0367
Iteration: 2400; Percent complete: 60.0%; Average loss: 2.9932
Iteration: 2401; Percent complete: 60.0%; Average loss: 3.2273
Iteration: 2402; Percent complete: 60.1%; Average loss: 3.0904
Iteration: 2403; Percent complete: 60.1%; Average loss: 2.9476
Iteration: 2404; Percent complete: 60.1%; Average loss: 3.0782
Iteration: 2405; Percent complete: 60.1%; Average loss: 3.0339
Iteration: 2406; Percent complete: 60.2%; Average loss: 3.0548
Iteration: 2407; Percent complete: 60.2%; Average loss: 3.1436
Iteration: 2408; Percent complete: 60.2%; Average loss: 3.1426
Iteration: 2409; Percent complete: 60.2%; Average loss: 2.9373
Iteration: 2410; Percent complete: 60.2%; Average loss: 2.8667
Iteration: 2411; Percent complete: 60.3%; Average loss: 3.1360
Iteration: 2412; Percent complete: 60.3%; Average loss: 2.9537
Iteration: 2413; Percent complete: 60.3%; Average loss: 3.0396
Iteration: 2414; Percent complete: 60.4%; Average loss: 2.8503
Iteration: 2415; Percent complete: 60.4%; Average loss: 3.1602
Iteration: 2416; Percent complete: 60.4%; Average loss: 3.0030
Iteration: 2417; Percent complete: 60.4%; Average loss: 2.8980
Iteration: 2418; Percent complete: 60.5%; Average loss: 3.3689
Iteration: 2419; Percent complete: 60.5%; Average loss: 2.8387
Iteration: 2420; Percent complete: 60.5%; Average loss: 3.0419
Iteration: 2421; Percent complete: 60.5%; Average loss: 2.9824
Iteration: 2422; Percent complete: 60.6%; Average loss: 2.9339
Iteration: 2423; Percent complete: 60.6%; Average loss: 3.0535
Iteration: 2424; Percent complete: 60.6%; Average loss: 3.1714
Iteration: 2425; Percent complete: 60.6%; Average loss: 3.0102
Iteration: 2426; Percent complete: 60.7%; Average loss: 3.1574
Iteration: 2427; Percent complete: 60.7%; Average loss: 3.0134
Iteration: 2428; Percent complete: 60.7%; Average loss: 3.4368
Iteration: 2429; Percent complete: 60.7%; Average loss: 2.8783
Iteration: 2430; Percent complete: 60.8%; Average loss: 3.4031
Iteration: 2431; Percent complete: 60.8%; Average loss: 2.6634
Iteration: 2432; Percent complete: 60.8%; Average loss: 2.9330
Iteration: 2433; Percent complete: 60.8%; Average loss: 3.2009
Iteration: 2434; Percent complete: 60.9%; Average loss: 3.1212
Iteration: 2435; Percent complete: 60.9%; Average loss: 3.4541
Iteration: 2436; Percent complete: 60.9%; Average loss: 2.9487
Iteration: 2437; Percent complete: 60.9%; Average loss: 2.9645
Iteration: 2438; Percent complete: 61.0%; Average loss: 3.1000
Iteration: 2439; Percent complete: 61.0%; Average loss: 2.9752
Iteration: 2440; Percent complete: 61.0%; Average loss: 2.8702
Iteration: 2441; Percent complete: 61.0%; Average loss: 3.0323
Iteration: 2442; Percent complete: 61.1%; Average loss: 2.8720
Iteration: 2443; Percent complete: 61.1%; Average loss: 3.1100
Iteration: 2444; Percent complete: 61.1%; Average loss: 3.0756
Iteration: 2445; Percent complete: 61.1%; Average loss: 2.8910
Iteration: 2446; Percent complete: 61.2%; Average loss: 2.8803
Iteration: 2447; Percent complete: 61.2%; Average loss: 2.9886
Iteration: 2448; Percent complete: 61.2%; Average loss: 2.9154
Iteration: 2449; Percent complete: 61.2%; Average loss: 2.8807
Iteration: 2450; Percent complete: 61.3%; Average loss: 3.2759
Iteration: 2451; Percent complete: 61.3%; Average loss: 2.9352
Iteration: 2452; Percent complete: 61.3%; Average loss: 2.8890
Iteration: 2453; Percent complete: 61.3%; Average loss: 3.1431
Iteration: 2454; Percent complete: 61.4%; Average loss: 3.0024
Iteration: 2455; Percent complete: 61.4%; Average loss: 3.2346
Iteration: 2456; Percent complete: 61.4%; Average loss: 3.1509
Iteration: 2457; Percent complete: 61.4%; Average loss: 2.9029
Iteration: 2458; Percent complete: 61.5%; Average loss: 3.0748
Iteration: 2459; Percent complete: 61.5%; Average loss: 3.2076
Iteration: 2460; Percent complete: 61.5%; Average loss: 3.0741
Iteration: 2461; Percent complete: 61.5%; Average loss: 2.9934
Iteration: 2462; Percent complete: 61.6%; Average loss: 2.7359
Iteration: 2463; Percent complete: 61.6%; Average loss: 3.0616
Iteration: 2464; Percent complete: 61.6%; Average loss: 2.9827
Iteration: 2465; Percent complete: 61.6%; Average loss: 2.8266
Iteration: 2466; Percent complete: 61.7%; Average loss: 3.2045
Iteration: 2467; Percent complete: 61.7%; Average loss: 3.0483
Iteration: 2468; Percent complete: 61.7%; Average loss: 2.8880
Iteration: 2469; Percent complete: 61.7%; Average loss: 2.9963
Iteration: 2470; Percent complete: 61.8%; Average loss: 3.0282
Iteration: 2471; Percent complete: 61.8%; Average loss: 2.9242
Iteration: 2472; Percent complete: 61.8%; Average loss: 3.0711
Iteration: 2473; Percent complete: 61.8%; Average loss: 3.3497
Iteration: 2474; Percent complete: 61.9%; Average loss: 2.9352
Iteration: 2475; Percent complete: 61.9%; Average loss: 2.8701
Iteration: 2476; Percent complete: 61.9%; Average loss: 3.2092
Iteration: 2477; Percent complete: 61.9%; Average loss: 2.9945
Iteration: 2478; Percent complete: 62.0%; Average loss: 3.2592
Iteration: 2479; Percent complete: 62.0%; Average loss: 3.2144
Iteration: 2480; Percent complete: 62.0%; Average loss: 3.2269
Iteration: 2481; Percent complete: 62.0%; Average loss: 3.0155
Iteration: 2482; Percent complete: 62.1%; Average loss: 3.0477
Iteration: 2483; Percent complete: 62.1%; Average loss: 3.2301
Iteration: 2484; Percent complete: 62.1%; Average loss: 3.0761
Iteration: 2485; Percent complete: 62.1%; Average loss: 3.1742
Iteration: 2486; Percent complete: 62.2%; Average loss: 3.0411
Iteration: 2487; Percent complete: 62.2%; Average loss: 3.1661
Iteration: 2488; Percent complete: 62.2%; Average loss: 3.2623
Iteration: 2489; Percent complete: 62.2%; Average loss: 2.8629
Iteration: 2490; Percent complete: 62.3%; Average loss: 3.2036
Iteration: 2491; Percent complete: 62.3%; Average loss: 3.0844
Iteration: 2492; Percent complete: 62.3%; Average loss: 2.8175
Iteration: 2493; Percent complete: 62.3%; Average loss: 2.8691
Iteration: 2494; Percent complete: 62.4%; Average loss: 2.9784
Iteration: 2495; Percent complete: 62.4%; Average loss: 3.0419
Iteration: 2496; Percent complete: 62.4%; Average loss: 3.1643
Iteration: 2497; Percent complete: 62.4%; Average loss: 3.1837
Iteration: 2498; Percent complete: 62.5%; Average loss: 3.4283
Iteration: 2499; Percent complete: 62.5%; Average loss: 3.2755
Iteration: 2500; Percent complete: 62.5%; Average loss: 2.8469
Iteration: 2501; Percent complete: 62.5%; Average loss: 3.0951
Iteration: 2502; Percent complete: 62.5%; Average loss: 2.9911
Iteration: 2503; Percent complete: 62.6%; Average loss: 3.1318
Iteration: 2504; Percent complete: 62.6%; Average loss: 3.1211
Iteration: 2505; Percent complete: 62.6%; Average loss: 2.7706
Iteration: 2506; Percent complete: 62.6%; Average loss: 3.1351
Iteration: 2507; Percent complete: 62.7%; Average loss: 2.8882
Iteration: 2508; Percent complete: 62.7%; Average loss: 3.3855
Iteration: 2509; Percent complete: 62.7%; Average loss: 3.0915
Iteration: 2510; Percent complete: 62.7%; Average loss: 3.0261
Iteration: 2511; Percent complete: 62.8%; Average loss: 2.9836
Iteration: 2512; Percent complete: 62.8%; Average loss: 2.9632
Iteration: 2513; Percent complete: 62.8%; Average loss: 3.0849
Iteration: 2514; Percent complete: 62.8%; Average loss: 3.0059
Iteration: 2515; Percent complete: 62.9%; Average loss: 2.9481
Iteration: 2516; Percent complete: 62.9%; Average loss: 2.9488
Iteration: 2517; Percent complete: 62.9%; Average loss: 3.1917
Iteration: 2518; Percent complete: 62.9%; Average loss: 2.9457
Iteration: 2519; Percent complete: 63.0%; Average loss: 3.2355
Iteration: 2520; Percent complete: 63.0%; Average loss: 3.1388
Iteration: 2521; Percent complete: 63.0%; Average loss: 3.1552
Iteration: 2522; Percent complete: 63.0%; Average loss: 2.9709
Iteration: 2523; Percent complete: 63.1%; Average loss: 3.0419
Iteration: 2524; Percent complete: 63.1%; Average loss: 3.1529
Iteration: 2525; Percent complete: 63.1%; Average loss: 3.1961
Iteration: 2526; Percent complete: 63.1%; Average loss: 2.9004
Iteration: 2527; Percent complete: 63.2%; Average loss: 2.8307
Iteration: 2528; Percent complete: 63.2%; Average loss: 2.9779
Iteration: 2529; Percent complete: 63.2%; Average loss: 2.8230
Iteration: 2530; Percent complete: 63.2%; Average loss: 2.9021
Iteration: 2531; Percent complete: 63.3%; Average loss: 3.0375
Iteration: 2532; Percent complete: 63.3%; Average loss: 2.8054
Iteration: 2533; Percent complete: 63.3%; Average loss: 2.9557
Iteration: 2534; Percent complete: 63.3%; Average loss: 2.9920
Iteration: 2535; Percent complete: 63.4%; Average loss: 2.9286
Iteration: 2536; Percent complete: 63.4%; Average loss: 2.9070
Iteration: 2537; Percent complete: 63.4%; Average loss: 3.0259
Iteration: 2538; Percent complete: 63.4%; Average loss: 2.8672
Iteration: 2539; Percent complete: 63.5%; Average loss: 2.9445
Iteration: 2540; Percent complete: 63.5%; Average loss: 2.9821
Iteration: 2541; Percent complete: 63.5%; Average loss: 2.9527
Iteration: 2542; Percent complete: 63.5%; Average loss: 3.0067
Iteration: 2543; Percent complete: 63.6%; Average loss: 3.0169
Iteration: 2544; Percent complete: 63.6%; Average loss: 3.2308
Iteration: 2545; Percent complete: 63.6%; Average loss: 3.1031
Iteration: 2546; Percent complete: 63.6%; Average loss: 2.9695
Iteration: 2547; Percent complete: 63.7%; Average loss: 3.1694
Iteration: 2548; Percent complete: 63.7%; Average loss: 3.2437
Iteration: 2549; Percent complete: 63.7%; Average loss: 2.8823
Iteration: 2550; Percent complete: 63.7%; Average loss: 2.9618
Iteration: 2551; Percent complete: 63.8%; Average loss: 3.0707
Iteration: 2552; Percent complete: 63.8%; Average loss: 2.8157
Iteration: 2553; Percent complete: 63.8%; Average loss: 2.8612
Iteration: 2554; Percent complete: 63.8%; Average loss: 3.1265
Iteration: 2555; Percent complete: 63.9%; Average loss: 2.9019
Iteration: 2556; Percent complete: 63.9%; Average loss: 2.9314
Iteration: 2557; Percent complete: 63.9%; Average loss: 3.1189
Iteration: 2558; Percent complete: 63.9%; Average loss: 3.2101
Iteration: 2559; Percent complete: 64.0%; Average loss: 2.9109
Iteration: 2560; Percent complete: 64.0%; Average loss: 3.0242
Iteration: 2561; Percent complete: 64.0%; Average loss: 2.8249
Iteration: 2562; Percent complete: 64.0%; Average loss: 2.8451
Iteration: 2563; Percent complete: 64.1%; Average loss: 3.2126
Iteration: 2564; Percent complete: 64.1%; Average loss: 3.0285
Iteration: 2565; Percent complete: 64.1%; Average loss: 3.0700
Iteration: 2566; Percent complete: 64.1%; Average loss: 2.8537
Iteration: 2567; Percent complete: 64.2%; Average loss: 3.1358
Iteration: 2568; Percent complete: 64.2%; Average loss: 3.1396
Iteration: 2569; Percent complete: 64.2%; Average loss: 2.8865
Iteration: 2570; Percent complete: 64.2%; Average loss: 2.8031
Iteration: 2571; Percent complete: 64.3%; Average loss: 2.9300
Iteration: 2572; Percent complete: 64.3%; Average loss: 2.9595
Iteration: 2573; Percent complete: 64.3%; Average loss: 2.8885
Iteration: 2574; Percent complete: 64.3%; Average loss: 2.9452
Iteration: 2575; Percent complete: 64.4%; Average loss: 2.8959
Iteration: 2576; Percent complete: 64.4%; Average loss: 2.9693
Iteration: 2577; Percent complete: 64.4%; Average loss: 2.9917
Iteration: 2578; Percent complete: 64.5%; Average loss: 2.9843
Iteration: 2579; Percent complete: 64.5%; Average loss: 3.0552
Iteration: 2580; Percent complete: 64.5%; Average loss: 3.1096
Iteration: 2581; Percent complete: 64.5%; Average loss: 3.1283
Iteration: 2582; Percent complete: 64.5%; Average loss: 3.0304
Iteration: 2583; Percent complete: 64.6%; Average loss: 3.0479
Iteration: 2584; Percent complete: 64.6%; Average loss: 2.9765
Iteration: 2585; Percent complete: 64.6%; Average loss: 3.1325
Iteration: 2586; Percent complete: 64.6%; Average loss: 3.1828
Iteration: 2587; Percent complete: 64.7%; Average loss: 3.0620
Iteration: 2588; Percent complete: 64.7%; Average loss: 3.0550
Iteration: 2589; Percent complete: 64.7%; Average loss: 2.8462
Iteration: 2590; Percent complete: 64.8%; Average loss: 2.8919
Iteration: 2591; Percent complete: 64.8%; Average loss: 3.0112
Iteration: 2592; Percent complete: 64.8%; Average loss: 3.0370
Iteration: 2593; Percent complete: 64.8%; Average loss: 3.2220
Iteration: 2594; Percent complete: 64.8%; Average loss: 2.9216
Iteration: 2595; Percent complete: 64.9%; Average loss: 2.9606
Iteration: 2596; Percent complete: 64.9%; Average loss: 3.1564
Iteration: 2597; Percent complete: 64.9%; Average loss: 3.0288
Iteration: 2598; Percent complete: 65.0%; Average loss: 2.9072
Iteration: 2599; Percent complete: 65.0%; Average loss: 3.2148
Iteration: 2600; Percent complete: 65.0%; Average loss: 2.9404
Iteration: 2601; Percent complete: 65.0%; Average loss: 2.9063
Iteration: 2602; Percent complete: 65.0%; Average loss: 3.0790
Iteration: 2603; Percent complete: 65.1%; Average loss: 3.0307
Iteration: 2604; Percent complete: 65.1%; Average loss: 2.9060
Iteration: 2605; Percent complete: 65.1%; Average loss: 2.9674
Iteration: 2606; Percent complete: 65.1%; Average loss: 2.7197
Iteration: 2607; Percent complete: 65.2%; Average loss: 3.0438
Iteration: 2608; Percent complete: 65.2%; Average loss: 2.8371
Iteration: 2609; Percent complete: 65.2%; Average loss: 3.1112
Iteration: 2610; Percent complete: 65.2%; Average loss: 2.8433
Iteration: 2611; Percent complete: 65.3%; Average loss: 3.2238
Iteration: 2612; Percent complete: 65.3%; Average loss: 3.1521
Iteration: 2613; Percent complete: 65.3%; Average loss: 2.9323
Iteration: 2614; Percent complete: 65.3%; Average loss: 2.9950
Iteration: 2615; Percent complete: 65.4%; Average loss: 2.9904
Iteration: 2616; Percent complete: 65.4%; Average loss: 2.9610
Iteration: 2617; Percent complete: 65.4%; Average loss: 2.8596
Iteration: 2618; Percent complete: 65.5%; Average loss: 3.1187
Iteration: 2619; Percent complete: 65.5%; Average loss: 3.0299
Iteration: 2620; Percent complete: 65.5%; Average loss: 2.9865
Iteration: 2621; Percent complete: 65.5%; Average loss: 2.7392
Iteration: 2622; Percent complete: 65.5%; Average loss: 2.6572
Iteration: 2623; Percent complete: 65.6%; Average loss: 2.9443
Iteration: 2624; Percent complete: 65.6%; Average loss: 3.0414
Iteration: 2625; Percent complete: 65.6%; Average loss: 3.1301
Iteration: 2626; Percent complete: 65.6%; Average loss: 3.1026
Iteration: 2627; Percent complete: 65.7%; Average loss: 3.0044
Iteration: 2628; Percent complete: 65.7%; Average loss: 2.9612
Iteration: 2629; Percent complete: 65.7%; Average loss: 2.9788
Iteration: 2630; Percent complete: 65.8%; Average loss: 2.5726
Iteration: 2631; Percent complete: 65.8%; Average loss: 3.0658
Iteration: 2632; Percent complete: 65.8%; Average loss: 2.6504
Iteration: 2633; Percent complete: 65.8%; Average loss: 3.0742
Iteration: 2634; Percent complete: 65.8%; Average loss: 2.8926
Iteration: 2635; Percent complete: 65.9%; Average loss: 2.9310
Iteration: 2636; Percent complete: 65.9%; Average loss: 3.1018
Iteration: 2637; Percent complete: 65.9%; Average loss: 2.7620
Iteration: 2638; Percent complete: 66.0%; Average loss: 2.7563
Iteration: 2639; Percent complete: 66.0%; Average loss: 2.8719
Iteration: 2640; Percent complete: 66.0%; Average loss: 3.0925
Iteration: 2641; Percent complete: 66.0%; Average loss: 2.9400
Iteration: 2642; Percent complete: 66.0%; Average loss: 3.0332
Iteration: 2643; Percent complete: 66.1%; Average loss: 3.0615
Iteration: 2644; Percent complete: 66.1%; Average loss: 2.9763
Iteration: 2645; Percent complete: 66.1%; Average loss: 2.8267
Iteration: 2646; Percent complete: 66.1%; Average loss: 3.0258
Iteration: 2647; Percent complete: 66.2%; Average loss: 3.0155
Iteration: 2648; Percent complete: 66.2%; Average loss: 3.1346
Iteration: 2649; Percent complete: 66.2%; Average loss: 3.0278
Iteration: 2650; Percent complete: 66.2%; Average loss: 2.9036
Iteration: 2651; Percent complete: 66.3%; Average loss: 3.1539
Iteration: 2652; Percent complete: 66.3%; Average loss: 2.9408
Iteration: 2653; Percent complete: 66.3%; Average loss: 2.8652
Iteration: 2654; Percent complete: 66.3%; Average loss: 2.8455
Iteration: 2655; Percent complete: 66.4%; Average loss: 2.9152
Iteration: 2656; Percent complete: 66.4%; Average loss: 2.8130
Iteration: 2657; Percent complete: 66.4%; Average loss: 2.8737
Iteration: 2658; Percent complete: 66.5%; Average loss: 3.1314
Iteration: 2659; Percent complete: 66.5%; Average loss: 2.8946
Iteration: 2660; Percent complete: 66.5%; Average loss: 3.1578
Iteration: 2661; Percent complete: 66.5%; Average loss: 2.8167
Iteration: 2662; Percent complete: 66.5%; Average loss: 2.9185
Iteration: 2663; Percent complete: 66.6%; Average loss: 3.1163
Iteration: 2664; Percent complete: 66.6%; Average loss: 2.7796
Iteration: 2665; Percent complete: 66.6%; Average loss: 2.7737
Iteration: 2666; Percent complete: 66.6%; Average loss: 3.2272
Iteration: 2667; Percent complete: 66.7%; Average loss: 3.0122
Iteration: 2668; Percent complete: 66.7%; Average loss: 3.0413
Iteration: 2669; Percent complete: 66.7%; Average loss: 3.0737
Iteration: 2670; Percent complete: 66.8%; Average loss: 3.0280
Iteration: 2671; Percent complete: 66.8%; Average loss: 3.3188
Iteration: 2672; Percent complete: 66.8%; Average loss: 3.0648
Iteration: 2673; Percent complete: 66.8%; Average loss: 2.9686
Iteration: 2674; Percent complete: 66.8%; Average loss: 2.9483
Iteration: 2675; Percent complete: 66.9%; Average loss: 2.8995
Iteration: 2676; Percent complete: 66.9%; Average loss: 3.0034
Iteration: 2677; Percent complete: 66.9%; Average loss: 2.8761
Iteration: 2678; Percent complete: 67.0%; Average loss: 2.9935
Iteration: 2679; Percent complete: 67.0%; Average loss: 3.1714
Iteration: 2680; Percent complete: 67.0%; Average loss: 3.1226
Iteration: 2681; Percent complete: 67.0%; Average loss: 3.0068
Iteration: 2682; Percent complete: 67.0%; Average loss: 3.0972
Iteration: 2683; Percent complete: 67.1%; Average loss: 3.0901
Iteration: 2684; Percent complete: 67.1%; Average loss: 3.0102
Iteration: 2685; Percent complete: 67.1%; Average loss: 2.8780
Iteration: 2686; Percent complete: 67.2%; Average loss: 2.8951
Iteration: 2687; Percent complete: 67.2%; Average loss: 2.9047
Iteration: 2688; Percent complete: 67.2%; Average loss: 2.7698
Iteration: 2689; Percent complete: 67.2%; Average loss: 3.0114
Iteration: 2690; Percent complete: 67.2%; Average loss: 2.8342
Iteration: 2691; Percent complete: 67.3%; Average loss: 3.0758
Iteration: 2692; Percent complete: 67.3%; Average loss: 3.0585
Iteration: 2693; Percent complete: 67.3%; Average loss: 3.0570
Iteration: 2694; Percent complete: 67.3%; Average loss: 3.1661
Iteration: 2695; Percent complete: 67.4%; Average loss: 3.0595
Iteration: 2696; Percent complete: 67.4%; Average loss: 2.9770
Iteration: 2697; Percent complete: 67.4%; Average loss: 2.9312
Iteration: 2698; Percent complete: 67.5%; Average loss: 3.1568
Iteration: 2699; Percent complete: 67.5%; Average loss: 3.1141
Iteration: 2700; Percent complete: 67.5%; Average loss: 2.9362
Iteration: 2701; Percent complete: 67.5%; Average loss: 2.9803
Iteration: 2702; Percent complete: 67.5%; Average loss: 2.8818
Iteration: 2703; Percent complete: 67.6%; Average loss: 3.1827
Iteration: 2704; Percent complete: 67.6%; Average loss: 3.1874
Iteration: 2705; Percent complete: 67.6%; Average loss: 2.9129
Iteration: 2706; Percent complete: 67.7%; Average loss: 2.9777
Iteration: 2707; Percent complete: 67.7%; Average loss: 2.8877
Iteration: 2708; Percent complete: 67.7%; Average loss: 2.9933
Iteration: 2709; Percent complete: 67.7%; Average loss: 2.8087
Iteration: 2710; Percent complete: 67.8%; Average loss: 3.1003
Iteration: 2711; Percent complete: 67.8%; Average loss: 3.0046
Iteration: 2712; Percent complete: 67.8%; Average loss: 3.0825
Iteration: 2713; Percent complete: 67.8%; Average loss: 2.8392
Iteration: 2714; Percent complete: 67.8%; Average loss: 3.0093
Iteration: 2715; Percent complete: 67.9%; Average loss: 2.8557
Iteration: 2716; Percent complete: 67.9%; Average loss: 3.0900
Iteration: 2717; Percent complete: 67.9%; Average loss: 3.0543
Iteration: 2718; Percent complete: 68.0%; Average loss: 2.8345
Iteration: 2719; Percent complete: 68.0%; Average loss: 3.1105
Iteration: 2720; Percent complete: 68.0%; Average loss: 3.1552
Iteration: 2721; Percent complete: 68.0%; Average loss: 2.9426
Iteration: 2722; Percent complete: 68.0%; Average loss: 3.1105
Iteration: 2723; Percent complete: 68.1%; Average loss: 2.8237
Iteration: 2724; Percent complete: 68.1%; Average loss: 2.8355
Iteration: 2725; Percent complete: 68.1%; Average loss: 2.7216
Iteration: 2726; Percent complete: 68.2%; Average loss: 3.0944
Iteration: 2727; Percent complete: 68.2%; Average loss: 3.1029
Iteration: 2728; Percent complete: 68.2%; Average loss: 2.8170
Iteration: 2729; Percent complete: 68.2%; Average loss: 2.7463
Iteration: 2730; Percent complete: 68.2%; Average loss: 3.0853
Iteration: 2731; Percent complete: 68.3%; Average loss: 2.8662
Iteration: 2732; Percent complete: 68.3%; Average loss: 2.9973
Iteration: 2733; Percent complete: 68.3%; Average loss: 2.9511
Iteration: 2734; Percent complete: 68.3%; Average loss: 2.7855
Iteration: 2735; Percent complete: 68.4%; Average loss: 3.1935
Iteration: 2736; Percent complete: 68.4%; Average loss: 2.7520
Iteration: 2737; Percent complete: 68.4%; Average loss: 3.1363
Iteration: 2738; Percent complete: 68.5%; Average loss: 2.8728
Iteration: 2739; Percent complete: 68.5%; Average loss: 2.7611
Iteration: 2740; Percent complete: 68.5%; Average loss: 3.2059
Iteration: 2741; Percent complete: 68.5%; Average loss: 3.0320
Iteration: 2742; Percent complete: 68.5%; Average loss: 3.1780
Iteration: 2743; Percent complete: 68.6%; Average loss: 2.8882
Iteration: 2744; Percent complete: 68.6%; Average loss: 2.8689
Iteration: 2745; Percent complete: 68.6%; Average loss: 2.9757
Iteration: 2746; Percent complete: 68.7%; Average loss: 3.0171
Iteration: 2747; Percent complete: 68.7%; Average loss: 2.9353
Iteration: 2748; Percent complete: 68.7%; Average loss: 2.9272
Iteration: 2749; Percent complete: 68.7%; Average loss: 2.7907
Iteration: 2750; Percent complete: 68.8%; Average loss: 3.0667
Iteration: 2751; Percent complete: 68.8%; Average loss: 3.1503
Iteration: 2752; Percent complete: 68.8%; Average loss: 3.0657
Iteration: 2753; Percent complete: 68.8%; Average loss: 2.9053
Iteration: 2754; Percent complete: 68.8%; Average loss: 3.0625
Iteration: 2755; Percent complete: 68.9%; Average loss: 2.9975
Iteration: 2756; Percent complete: 68.9%; Average loss: 2.8588
Iteration: 2757; Percent complete: 68.9%; Average loss: 3.1216
Iteration: 2758; Percent complete: 69.0%; Average loss: 2.7419
Iteration: 2759; Percent complete: 69.0%; Average loss: 2.9136
Iteration: 2760; Percent complete: 69.0%; Average loss: 2.9302
Iteration: 2761; Percent complete: 69.0%; Average loss: 2.9301
Iteration: 2762; Percent complete: 69.0%; Average loss: 2.8318
Iteration: 2763; Percent complete: 69.1%; Average loss: 2.8584
Iteration: 2764; Percent complete: 69.1%; Average loss: 2.9020
Iteration: 2765; Percent complete: 69.1%; Average loss: 2.7824
Iteration: 2766; Percent complete: 69.2%; Average loss: 2.9050
Iteration: 2767; Percent complete: 69.2%; Average loss: 2.7811
Iteration: 2768; Percent complete: 69.2%; Average loss: 2.9587
Iteration: 2769; Percent complete: 69.2%; Average loss: 2.9680
Iteration: 2770; Percent complete: 69.2%; Average loss: 2.9165
Iteration: 2771; Percent complete: 69.3%; Average loss: 2.9406
Iteration: 2772; Percent complete: 69.3%; Average loss: 2.8235
Iteration: 2773; Percent complete: 69.3%; Average loss: 3.0387
Iteration: 2774; Percent complete: 69.3%; Average loss: 2.8275
Iteration: 2775; Percent complete: 69.4%; Average loss: 3.0834
Iteration: 2776; Percent complete: 69.4%; Average loss: 2.7729
Iteration: 2777; Percent complete: 69.4%; Average loss: 2.8493
Iteration: 2778; Percent complete: 69.5%; Average loss: 2.9674
Iteration: 2779; Percent complete: 69.5%; Average loss: 3.0876
Iteration: 2780; Percent complete: 69.5%; Average loss: 2.9168
Iteration: 2781; Percent complete: 69.5%; Average loss: 2.9542
Iteration: 2782; Percent complete: 69.5%; Average loss: 2.9074
Iteration: 2783; Percent complete: 69.6%; Average loss: 2.9956
Iteration: 2784; Percent complete: 69.6%; Average loss: 2.9581
Iteration: 2785; Percent complete: 69.6%; Average loss: 2.8357
Iteration: 2786; Percent complete: 69.7%; Average loss: 2.8111
Iteration: 2787; Percent complete: 69.7%; Average loss: 2.9015
Iteration: 2788; Percent complete: 69.7%; Average loss: 2.8797
Iteration: 2789; Percent complete: 69.7%; Average loss: 3.0426
Iteration: 2790; Percent complete: 69.8%; Average loss: 3.0083
Iteration: 2791; Percent complete: 69.8%; Average loss: 2.8965
Iteration: 2792; Percent complete: 69.8%; Average loss: 2.8127
Iteration: 2793; Percent complete: 69.8%; Average loss: 3.1696
Iteration: 2794; Percent complete: 69.8%; Average loss: 2.9643
Iteration: 2795; Percent complete: 69.9%; Average loss: 3.0067
Iteration: 2796; Percent complete: 69.9%; Average loss: 2.9820
Iteration: 2797; Percent complete: 69.9%; Average loss: 3.0633
Iteration: 2798; Percent complete: 70.0%; Average loss: 3.1024
Iteration: 2799; Percent complete: 70.0%; Average loss: 3.0066
Iteration: 2800; Percent complete: 70.0%; Average loss: 2.9492
Iteration: 2801; Percent complete: 70.0%; Average loss: 2.8744
Iteration: 2802; Percent complete: 70.0%; Average loss: 2.7831
Iteration: 2803; Percent complete: 70.1%; Average loss: 3.0239
Iteration: 2804; Percent complete: 70.1%; Average loss: 3.0004
Iteration: 2805; Percent complete: 70.1%; Average loss: 3.0503
Iteration: 2806; Percent complete: 70.2%; Average loss: 2.8164
Iteration: 2807; Percent complete: 70.2%; Average loss: 2.7798
Iteration: 2808; Percent complete: 70.2%; Average loss: 2.8994
Iteration: 2809; Percent complete: 70.2%; Average loss: 2.9435
Iteration: 2810; Percent complete: 70.2%; Average loss: 2.9237
Iteration: 2811; Percent complete: 70.3%; Average loss: 3.0063
Iteration: 2812; Percent complete: 70.3%; Average loss: 2.8979
Iteration: 2813; Percent complete: 70.3%; Average loss: 2.7559
Iteration: 2814; Percent complete: 70.3%; Average loss: 2.9786
Iteration: 2815; Percent complete: 70.4%; Average loss: 3.3768
Iteration: 2816; Percent complete: 70.4%; Average loss: 2.7673
Iteration: 2817; Percent complete: 70.4%; Average loss: 2.8771
Iteration: 2818; Percent complete: 70.5%; Average loss: 2.9218
Iteration: 2819; Percent complete: 70.5%; Average loss: 2.9225
Iteration: 2820; Percent complete: 70.5%; Average loss: 2.7900
Iteration: 2821; Percent complete: 70.5%; Average loss: 3.0329
Iteration: 2822; Percent complete: 70.5%; Average loss: 3.0218
Iteration: 2823; Percent complete: 70.6%; Average loss: 2.7197
Iteration: 2824; Percent complete: 70.6%; Average loss: 3.0754
Iteration: 2825; Percent complete: 70.6%; Average loss: 3.0565
Iteration: 2826; Percent complete: 70.7%; Average loss: 2.9934
Iteration: 2827; Percent complete: 70.7%; Average loss: 2.8854
Iteration: 2828; Percent complete: 70.7%; Average loss: 3.1870
Iteration: 2829; Percent complete: 70.7%; Average loss: 2.9460
Iteration: 2830; Percent complete: 70.8%; Average loss: 2.8455
Iteration: 2831; Percent complete: 70.8%; Average loss: 2.7182
Iteration: 2832; Percent complete: 70.8%; Average loss: 3.1834
Iteration: 2833; Percent complete: 70.8%; Average loss: 2.9802
Iteration: 2834; Percent complete: 70.9%; Average loss: 2.8474
Iteration: 2835; Percent complete: 70.9%; Average loss: 2.8460
Iteration: 2836; Percent complete: 70.9%; Average loss: 2.7649
Iteration: 2837; Percent complete: 70.9%; Average loss: 3.0192
Iteration: 2838; Percent complete: 71.0%; Average loss: 3.1456
Iteration: 2839; Percent complete: 71.0%; Average loss: 2.9335
Iteration: 2840; Percent complete: 71.0%; Average loss: 3.0682
Iteration: 2841; Percent complete: 71.0%; Average loss: 3.0500
Iteration: 2842; Percent complete: 71.0%; Average loss: 2.7596
Iteration: 2843; Percent complete: 71.1%; Average loss: 3.0721
Iteration: 2844; Percent complete: 71.1%; Average loss: 3.1020
Iteration: 2845; Percent complete: 71.1%; Average loss: 2.9368
Iteration: 2846; Percent complete: 71.2%; Average loss: 2.9775
Iteration: 2847; Percent complete: 71.2%; Average loss: 3.0011
Iteration: 2848; Percent complete: 71.2%; Average loss: 2.8455
Iteration: 2849; Percent complete: 71.2%; Average loss: 2.9528
Iteration: 2850; Percent complete: 71.2%; Average loss: 3.0648
Iteration: 2851; Percent complete: 71.3%; Average loss: 2.9831
Iteration: 2852; Percent complete: 71.3%; Average loss: 3.2153
Iteration: 2853; Percent complete: 71.3%; Average loss: 2.9774
Iteration: 2854; Percent complete: 71.4%; Average loss: 2.9667
Iteration: 2855; Percent complete: 71.4%; Average loss: 3.1321
Iteration: 2856; Percent complete: 71.4%; Average loss: 2.9603
Iteration: 2857; Percent complete: 71.4%; Average loss: 2.8391
Iteration: 2858; Percent complete: 71.5%; Average loss: 2.8869
Iteration: 2859; Percent complete: 71.5%; Average loss: 2.8782
Iteration: 2860; Percent complete: 71.5%; Average loss: 2.9166
Iteration: 2861; Percent complete: 71.5%; Average loss: 3.0327
Iteration: 2862; Percent complete: 71.5%; Average loss: 2.9668
Iteration: 2863; Percent complete: 71.6%; Average loss: 2.8286
Iteration: 2864; Percent complete: 71.6%; Average loss: 2.9030
Iteration: 2865; Percent complete: 71.6%; Average loss: 2.9817
Iteration: 2866; Percent complete: 71.7%; Average loss: 3.0957
Iteration: 2867; Percent complete: 71.7%; Average loss: 2.9215
Iteration: 2868; Percent complete: 71.7%; Average loss: 2.9513
Iteration: 2869; Percent complete: 71.7%; Average loss: 2.9620
Iteration: 2870; Percent complete: 71.8%; Average loss: 2.9418
Iteration: 2871; Percent complete: 71.8%; Average loss: 2.9101
Iteration: 2872; Percent complete: 71.8%; Average loss: 2.9368
Iteration: 2873; Percent complete: 71.8%; Average loss: 2.9804
Iteration: 2874; Percent complete: 71.9%; Average loss: 2.6968
Iteration: 2875; Percent complete: 71.9%; Average loss: 3.1909
Iteration: 2876; Percent complete: 71.9%; Average loss: 3.0780
Iteration: 2877; Percent complete: 71.9%; Average loss: 2.7917
Iteration: 2878; Percent complete: 72.0%; Average loss: 3.4161
Iteration: 2879; Percent complete: 72.0%; Average loss: 2.9835
Iteration: 2880; Percent complete: 72.0%; Average loss: 2.8038
Iteration: 2881; Percent complete: 72.0%; Average loss: 2.7909
Iteration: 2882; Percent complete: 72.0%; Average loss: 3.0081
Iteration: 2883; Percent complete: 72.1%; Average loss: 2.7755
Iteration: 2884; Percent complete: 72.1%; Average loss: 2.9306
Iteration: 2885; Percent complete: 72.1%; Average loss: 2.9950
Iteration: 2886; Percent complete: 72.2%; Average loss: 2.6653
Iteration: 2887; Percent complete: 72.2%; Average loss: 2.9034
Iteration: 2888; Percent complete: 72.2%; Average loss: 3.0081
Iteration: 2889; Percent complete: 72.2%; Average loss: 2.7613
Iteration: 2890; Percent complete: 72.2%; Average loss: 2.9265
Iteration: 2891; Percent complete: 72.3%; Average loss: 3.0815
Iteration: 2892; Percent complete: 72.3%; Average loss: 3.2231
Iteration: 2893; Percent complete: 72.3%; Average loss: 2.8843
Iteration: 2894; Percent complete: 72.4%; Average loss: 2.9722
Iteration: 2895; Percent complete: 72.4%; Average loss: 2.8474
Iteration: 2896; Percent complete: 72.4%; Average loss: 2.7546
Iteration: 2897; Percent complete: 72.4%; Average loss: 3.0856
Iteration: 2898; Percent complete: 72.5%; Average loss: 3.0442
Iteration: 2899; Percent complete: 72.5%; Average loss: 3.1043
Iteration: 2900; Percent complete: 72.5%; Average loss: 2.9120
Iteration: 2901; Percent complete: 72.5%; Average loss: 2.7574
Iteration: 2902; Percent complete: 72.5%; Average loss: 3.0043
Iteration: 2903; Percent complete: 72.6%; Average loss: 3.0004
Iteration: 2904; Percent complete: 72.6%; Average loss: 2.9842
Iteration: 2905; Percent complete: 72.6%; Average loss: 2.7686
Iteration: 2906; Percent complete: 72.7%; Average loss: 3.0387
Iteration: 2907; Percent complete: 72.7%; Average loss: 2.9843
Iteration: 2908; Percent complete: 72.7%; Average loss: 2.9929
Iteration: 2909; Percent complete: 72.7%; Average loss: 3.0259
Iteration: 2910; Percent complete: 72.8%; Average loss: 3.0942
Iteration: 2911; Percent complete: 72.8%; Average loss: 3.1884
Iteration: 2912; Percent complete: 72.8%; Average loss: 2.9708
Iteration: 2913; Percent complete: 72.8%; Average loss: 2.9501
Iteration: 2914; Percent complete: 72.9%; Average loss: 2.8006
Iteration: 2915; Percent complete: 72.9%; Average loss: 2.9893
Iteration: 2916; Percent complete: 72.9%; Average loss: 2.9852
Iteration: 2917; Percent complete: 72.9%; Average loss: 2.8412
Iteration: 2918; Percent complete: 73.0%; Average loss: 2.9369
Iteration: 2919; Percent complete: 73.0%; Average loss: 3.0047
Iteration: 2920; Percent complete: 73.0%; Average loss: 2.8472
Iteration: 2921; Percent complete: 73.0%; Average loss: 2.7200
Iteration: 2922; Percent complete: 73.0%; Average loss: 3.1742
Iteration: 2923; Percent complete: 73.1%; Average loss: 2.8671
Iteration: 2924; Percent complete: 73.1%; Average loss: 3.2303
Iteration: 2925; Percent complete: 73.1%; Average loss: 3.0130
Iteration: 2926; Percent complete: 73.2%; Average loss: 2.8770
Iteration: 2927; Percent complete: 73.2%; Average loss: 2.8482
Iteration: 2928; Percent complete: 73.2%; Average loss: 2.9228
Iteration: 2929; Percent complete: 73.2%; Average loss: 2.9515
Iteration: 2930; Percent complete: 73.2%; Average loss: 2.8134
Iteration: 2931; Percent complete: 73.3%; Average loss: 2.9495
Iteration: 2932; Percent complete: 73.3%; Average loss: 3.0097
Iteration: 2933; Percent complete: 73.3%; Average loss: 2.9478
Iteration: 2934; Percent complete: 73.4%; Average loss: 3.0476
Iteration: 2935; Percent complete: 73.4%; Average loss: 2.8829
Iteration: 2936; Percent complete: 73.4%; Average loss: 2.8689
Iteration: 2937; Percent complete: 73.4%; Average loss: 3.0727
Iteration: 2938; Percent complete: 73.5%; Average loss: 2.8782
Iteration: 2939; Percent complete: 73.5%; Average loss: 2.7639
Iteration: 2940; Percent complete: 73.5%; Average loss: 3.2596
Iteration: 2941; Percent complete: 73.5%; Average loss: 2.8128
Iteration: 2942; Percent complete: 73.6%; Average loss: 2.9740
Iteration: 2943; Percent complete: 73.6%; Average loss: 2.8112
Iteration: 2944; Percent complete: 73.6%; Average loss: 3.0119
Iteration: 2945; Percent complete: 73.6%; Average loss: 2.7524
Iteration: 2946; Percent complete: 73.7%; Average loss: 3.1963
Iteration: 2947; Percent complete: 73.7%; Average loss: 2.8196
Iteration: 2948; Percent complete: 73.7%; Average loss: 3.0428
Iteration: 2949; Percent complete: 73.7%; Average loss: 2.7477
Iteration: 2950; Percent complete: 73.8%; Average loss: 2.9984
Iteration: 2951; Percent complete: 73.8%; Average loss: 2.9821
Iteration: 2952; Percent complete: 73.8%; Average loss: 2.8199
Iteration: 2953; Percent complete: 73.8%; Average loss: 2.7825
Iteration: 2954; Percent complete: 73.9%; Average loss: 2.7553
Iteration: 2955; Percent complete: 73.9%; Average loss: 2.9605
Iteration: 2956; Percent complete: 73.9%; Average loss: 2.8169
Iteration: 2957; Percent complete: 73.9%; Average loss: 3.0633
Iteration: 2958; Percent complete: 74.0%; Average loss: 2.9021
Iteration: 2959; Percent complete: 74.0%; Average loss: 2.9216
Iteration: 2960; Percent complete: 74.0%; Average loss: 2.8160
Iteration: 2961; Percent complete: 74.0%; Average loss: 2.8465
Iteration: 2962; Percent complete: 74.1%; Average loss: 2.9651
Iteration: 2963; Percent complete: 74.1%; Average loss: 3.0615
Iteration: 2964; Percent complete: 74.1%; Average loss: 3.2393
Iteration: 2965; Percent complete: 74.1%; Average loss: 2.8738
Iteration: 2966; Percent complete: 74.2%; Average loss: 2.7007
Iteration: 2967; Percent complete: 74.2%; Average loss: 3.0605
Iteration: 2968; Percent complete: 74.2%; Average loss: 2.7832
Iteration: 2969; Percent complete: 74.2%; Average loss: 2.9274
Iteration: 2970; Percent complete: 74.2%; Average loss: 2.9265
Iteration: 2971; Percent complete: 74.3%; Average loss: 2.9793
Iteration: 2972; Percent complete: 74.3%; Average loss: 2.9507
Iteration: 2973; Percent complete: 74.3%; Average loss: 2.7875
Iteration: 2974; Percent complete: 74.4%; Average loss: 2.6126
Iteration: 2975; Percent complete: 74.4%; Average loss: 2.8418
Iteration: 2976; Percent complete: 74.4%; Average loss: 2.8067
Iteration: 2977; Percent complete: 74.4%; Average loss: 2.7482
Iteration: 2978; Percent complete: 74.5%; Average loss: 3.0664
Iteration: 2979; Percent complete: 74.5%; Average loss: 2.8175
Iteration: 2980; Percent complete: 74.5%; Average loss: 2.9275
Iteration: 2981; Percent complete: 74.5%; Average loss: 2.8175
Iteration: 2982; Percent complete: 74.6%; Average loss: 3.2226
Iteration: 2983; Percent complete: 74.6%; Average loss: 2.7740
Iteration: 2984; Percent complete: 74.6%; Average loss: 2.7958
Iteration: 2985; Percent complete: 74.6%; Average loss: 2.9179
Iteration: 2986; Percent complete: 74.7%; Average loss: 3.0359
Iteration: 2987; Percent complete: 74.7%; Average loss: 2.7052
Iteration: 2988; Percent complete: 74.7%; Average loss: 2.8567
Iteration: 2989; Percent complete: 74.7%; Average loss: 2.8686
Iteration: 2990; Percent complete: 74.8%; Average loss: 2.9092
Iteration: 2991; Percent complete: 74.8%; Average loss: 2.8800
Iteration: 2992; Percent complete: 74.8%; Average loss: 3.0886
Iteration: 2993; Percent complete: 74.8%; Average loss: 2.9374
Iteration: 2994; Percent complete: 74.9%; Average loss: 3.1257
Iteration: 2995; Percent complete: 74.9%; Average loss: 3.0579
Iteration: 2996; Percent complete: 74.9%; Average loss: 2.9682
Iteration: 2997; Percent complete: 74.9%; Average loss: 2.5902
Iteration: 2998; Percent complete: 75.0%; Average loss: 2.9372
Iteration: 2999; Percent complete: 75.0%; Average loss: 3.0703
Iteration: 3000; Percent complete: 75.0%; Average loss: 2.8887
Iteration: 3001; Percent complete: 75.0%; Average loss: 2.8122
Iteration: 3002; Percent complete: 75.0%; Average loss: 2.8944
Iteration: 3003; Percent complete: 75.1%; Average loss: 2.7278
Iteration: 3004; Percent complete: 75.1%; Average loss: 2.8793
Iteration: 3005; Percent complete: 75.1%; Average loss: 2.9571
Iteration: 3006; Percent complete: 75.1%; Average loss: 2.7808
Iteration: 3007; Percent complete: 75.2%; Average loss: 3.1320
Iteration: 3008; Percent complete: 75.2%; Average loss: 2.8459
Iteration: 3009; Percent complete: 75.2%; Average loss: 2.6653
Iteration: 3010; Percent complete: 75.2%; Average loss: 2.9511
Iteration: 3011; Percent complete: 75.3%; Average loss: 2.7860
Iteration: 3012; Percent complete: 75.3%; Average loss: 2.8463
Iteration: 3013; Percent complete: 75.3%; Average loss: 2.7489
Iteration: 3014; Percent complete: 75.3%; Average loss: 2.9780
Iteration: 3015; Percent complete: 75.4%; Average loss: 2.9205
Iteration: 3016; Percent complete: 75.4%; Average loss: 2.9860
Iteration: 3017; Percent complete: 75.4%; Average loss: 3.0433
Iteration: 3018; Percent complete: 75.4%; Average loss: 2.9950
Iteration: 3019; Percent complete: 75.5%; Average loss: 2.9832
Iteration: 3020; Percent complete: 75.5%; Average loss: 2.9545
Iteration: 3021; Percent complete: 75.5%; Average loss: 2.7340
Iteration: 3022; Percent complete: 75.5%; Average loss: 2.8102
Iteration: 3023; Percent complete: 75.6%; Average loss: 3.0798
Iteration: 3024; Percent complete: 75.6%; Average loss: 3.2080
Iteration: 3025; Percent complete: 75.6%; Average loss: 2.8417
Iteration: 3026; Percent complete: 75.6%; Average loss: 2.8850
Iteration: 3027; Percent complete: 75.7%; Average loss: 2.8050
Iteration: 3028; Percent complete: 75.7%; Average loss: 3.0391
Iteration: 3029; Percent complete: 75.7%; Average loss: 2.8129
Iteration: 3030; Percent complete: 75.8%; Average loss: 2.8483
Iteration: 3031; Percent complete: 75.8%; Average loss: 3.1591
Iteration: 3032; Percent complete: 75.8%; Average loss: 2.7540
Iteration: 3033; Percent complete: 75.8%; Average loss: 2.7776
Iteration: 3034; Percent complete: 75.8%; Average loss: 2.7762
Iteration: 3035; Percent complete: 75.9%; Average loss: 3.1450
Iteration: 3036; Percent complete: 75.9%; Average loss: 3.1000
Iteration: 3037; Percent complete: 75.9%; Average loss: 2.7898
Iteration: 3038; Percent complete: 75.9%; Average loss: 3.0752
Iteration: 3039; Percent complete: 76.0%; Average loss: 3.0073
Iteration: 3040; Percent complete: 76.0%; Average loss: 2.9400
Iteration: 3041; Percent complete: 76.0%; Average loss: 2.7984
Iteration: 3042; Percent complete: 76.0%; Average loss: 2.8646
Iteration: 3043; Percent complete: 76.1%; Average loss: 2.7813
Iteration: 3044; Percent complete: 76.1%; Average loss: 2.9671
Iteration: 3045; Percent complete: 76.1%; Average loss: 2.9558
Iteration: 3046; Percent complete: 76.1%; Average loss: 2.9179
Iteration: 3047; Percent complete: 76.2%; Average loss: 2.9603
Iteration: 3048; Percent complete: 76.2%; Average loss: 3.0371
Iteration: 3049; Percent complete: 76.2%; Average loss: 2.8993
Iteration: 3050; Percent complete: 76.2%; Average loss: 2.6834
Iteration: 3051; Percent complete: 76.3%; Average loss: 2.7944
Iteration: 3052; Percent complete: 76.3%; Average loss: 2.6917
Iteration: 3053; Percent complete: 76.3%; Average loss: 2.9693
Iteration: 3054; Percent complete: 76.3%; Average loss: 2.6472
Iteration: 3055; Percent complete: 76.4%; Average loss: 2.6655
Iteration: 3056; Percent complete: 76.4%; Average loss: 2.6954
Iteration: 3057; Percent complete: 76.4%; Average loss: 2.7983
Iteration: 3058; Percent complete: 76.4%; Average loss: 2.8538
Iteration: 3059; Percent complete: 76.5%; Average loss: 2.6187
Iteration: 3060; Percent complete: 76.5%; Average loss: 2.6628
Iteration: 3061; Percent complete: 76.5%; Average loss: 3.1186
Iteration: 3062; Percent complete: 76.5%; Average loss: 2.8391
Iteration: 3063; Percent complete: 76.6%; Average loss: 2.8061
Iteration: 3064; Percent complete: 76.6%; Average loss: 2.7169
Iteration: 3065; Percent complete: 76.6%; Average loss: 2.9765
Iteration: 3066; Percent complete: 76.6%; Average loss: 3.1186
Iteration: 3067; Percent complete: 76.7%; Average loss: 2.9398
Iteration: 3068; Percent complete: 76.7%; Average loss: 2.8251
Iteration: 3069; Percent complete: 76.7%; Average loss: 2.8839
Iteration: 3070; Percent complete: 76.8%; Average loss: 2.9495
Iteration: 3071; Percent complete: 76.8%; Average loss: 2.7041
Iteration: 3072; Percent complete: 76.8%; Average loss: 3.1836
Iteration: 3073; Percent complete: 76.8%; Average loss: 2.8016
Iteration: 3074; Percent complete: 76.8%; Average loss: 2.8210
Iteration: 3075; Percent complete: 76.9%; Average loss: 2.8973
Iteration: 3076; Percent complete: 76.9%; Average loss: 3.0744
Iteration: 3077; Percent complete: 76.9%; Average loss: 2.7131
Iteration: 3078; Percent complete: 77.0%; Average loss: 2.8301
Iteration: 3079; Percent complete: 77.0%; Average loss: 3.1767
Iteration: 3080; Percent complete: 77.0%; Average loss: 2.9283
Iteration: 3081; Percent complete: 77.0%; Average loss: 2.9093
Iteration: 3082; Percent complete: 77.0%; Average loss: 2.8142
Iteration: 3083; Percent complete: 77.1%; Average loss: 2.7300
Iteration: 3084; Percent complete: 77.1%; Average loss: 3.0601
Iteration: 3085; Percent complete: 77.1%; Average loss: 2.9332
Iteration: 3086; Percent complete: 77.1%; Average loss: 2.7573
Iteration: 3087; Percent complete: 77.2%; Average loss: 2.9109
Iteration: 3088; Percent complete: 77.2%; Average loss: 2.7621
Iteration: 3089; Percent complete: 77.2%; Average loss: 2.7443
Iteration: 3090; Percent complete: 77.2%; Average loss: 2.7437
Iteration: 3091; Percent complete: 77.3%; Average loss: 2.7891
Iteration: 3092; Percent complete: 77.3%; Average loss: 2.7869
Iteration: 3093; Percent complete: 77.3%; Average loss: 3.0321
Iteration: 3094; Percent complete: 77.3%; Average loss: 2.8710
Iteration: 3095; Percent complete: 77.4%; Average loss: 2.8685
Iteration: 3096; Percent complete: 77.4%; Average loss: 2.7568
Iteration: 3097; Percent complete: 77.4%; Average loss: 2.8794
Iteration: 3098; Percent complete: 77.5%; Average loss: 2.8716
Iteration: 3099; Percent complete: 77.5%; Average loss: 2.8737
Iteration: 3100; Percent complete: 77.5%; Average loss: 2.9639
Iteration: 3101; Percent complete: 77.5%; Average loss: 3.0109
Iteration: 3102; Percent complete: 77.5%; Average loss: 2.7275
Iteration: 3103; Percent complete: 77.6%; Average loss: 2.8194
Iteration: 3104; Percent complete: 77.6%; Average loss: 2.8361
Iteration: 3105; Percent complete: 77.6%; Average loss: 2.9743
Iteration: 3106; Percent complete: 77.6%; Average loss: 2.8242
Iteration: 3107; Percent complete: 77.7%; Average loss: 2.7450
Iteration: 3108; Percent complete: 77.7%; Average loss: 2.8891
Iteration: 3109; Percent complete: 77.7%; Average loss: 2.8579
Iteration: 3110; Percent complete: 77.8%; Average loss: 2.7784
Iteration: 3111; Percent complete: 77.8%; Average loss: 3.1762
Iteration: 3112; Percent complete: 77.8%; Average loss: 2.9133
Iteration: 3113; Percent complete: 77.8%; Average loss: 2.9512
Iteration: 3114; Percent complete: 77.8%; Average loss: 2.9664
Iteration: 3115; Percent complete: 77.9%; Average loss: 3.0476
Iteration: 3116; Percent complete: 77.9%; Average loss: 3.1413
Iteration: 3117; Percent complete: 77.9%; Average loss: 2.7485
Iteration: 3118; Percent complete: 78.0%; Average loss: 2.9627
Iteration: 3119; Percent complete: 78.0%; Average loss: 2.9370
Iteration: 3120; Percent complete: 78.0%; Average loss: 3.0408
Iteration: 3121; Percent complete: 78.0%; Average loss: 2.7920
Iteration: 3122; Percent complete: 78.0%; Average loss: 2.7864
Iteration: 3123; Percent complete: 78.1%; Average loss: 3.0136
Iteration: 3124; Percent complete: 78.1%; Average loss: 2.9377
Iteration: 3125; Percent complete: 78.1%; Average loss: 2.6499
Iteration: 3126; Percent complete: 78.1%; Average loss: 2.7805
Iteration: 3127; Percent complete: 78.2%; Average loss: 2.9087
Iteration: 3128; Percent complete: 78.2%; Average loss: 2.9108
Iteration: 3129; Percent complete: 78.2%; Average loss: 2.8398
Iteration: 3130; Percent complete: 78.2%; Average loss: 2.9257
Iteration: 3131; Percent complete: 78.3%; Average loss: 2.8338
Iteration: 3132; Percent complete: 78.3%; Average loss: 2.8820
Iteration: 3133; Percent complete: 78.3%; Average loss: 2.8629
Iteration: 3134; Percent complete: 78.3%; Average loss: 3.1625
Iteration: 3135; Percent complete: 78.4%; Average loss: 2.6676
Iteration: 3136; Percent complete: 78.4%; Average loss: 2.8374
Iteration: 3137; Percent complete: 78.4%; Average loss: 2.7474
Iteration: 3138; Percent complete: 78.5%; Average loss: 3.0164
Iteration: 3139; Percent complete: 78.5%; Average loss: 2.9276
Iteration: 3140; Percent complete: 78.5%; Average loss: 2.6933
Iteration: 3141; Percent complete: 78.5%; Average loss: 2.8578
Iteration: 3142; Percent complete: 78.5%; Average loss: 2.9140
Iteration: 3143; Percent complete: 78.6%; Average loss: 2.9662
Iteration: 3144; Percent complete: 78.6%; Average loss: 2.8672
Iteration: 3145; Percent complete: 78.6%; Average loss: 2.9300
Iteration: 3146; Percent complete: 78.6%; Average loss: 2.8725
Iteration: 3147; Percent complete: 78.7%; Average loss: 2.5997
Iteration: 3148; Percent complete: 78.7%; Average loss: 2.9304
Iteration: 3149; Percent complete: 78.7%; Average loss: 2.8753
Iteration: 3150; Percent complete: 78.8%; Average loss: 2.7390
Iteration: 3151; Percent complete: 78.8%; Average loss: 2.9343
Iteration: 3152; Percent complete: 78.8%; Average loss: 2.9882
Iteration: 3153; Percent complete: 78.8%; Average loss: 2.8001
Iteration: 3154; Percent complete: 78.8%; Average loss: 2.7803
Iteration: 3155; Percent complete: 78.9%; Average loss: 3.1542
Iteration: 3156; Percent complete: 78.9%; Average loss: 2.7485
Iteration: 3157; Percent complete: 78.9%; Average loss: 2.6992
Iteration: 3158; Percent complete: 79.0%; Average loss: 2.8680
Iteration: 3159; Percent complete: 79.0%; Average loss: 2.5625
Iteration: 3160; Percent complete: 79.0%; Average loss: 2.8248
Iteration: 3161; Percent complete: 79.0%; Average loss: 3.0470
Iteration: 3162; Percent complete: 79.0%; Average loss: 2.6046
Iteration: 3163; Percent complete: 79.1%; Average loss: 2.5820
Iteration: 3164; Percent complete: 79.1%; Average loss: 2.8148
Iteration: 3165; Percent complete: 79.1%; Average loss: 2.8255
Iteration: 3166; Percent complete: 79.1%; Average loss: 2.8192
Iteration: 3167; Percent complete: 79.2%; Average loss: 2.9429
Iteration: 3168; Percent complete: 79.2%; Average loss: 2.6418
Iteration: 3169; Percent complete: 79.2%; Average loss: 2.8953
Iteration: 3170; Percent complete: 79.2%; Average loss: 2.6860
Iteration: 3171; Percent complete: 79.3%; Average loss: 2.9436
Iteration: 3172; Percent complete: 79.3%; Average loss: 2.8787
Iteration: 3173; Percent complete: 79.3%; Average loss: 2.7139
Iteration: 3174; Percent complete: 79.3%; Average loss: 3.0794
Iteration: 3175; Percent complete: 79.4%; Average loss: 2.9729
Iteration: 3176; Percent complete: 79.4%; Average loss: 3.0619
Iteration: 3177; Percent complete: 79.4%; Average loss: 2.8278
Iteration: 3178; Percent complete: 79.5%; Average loss: 2.9375
Iteration: 3179; Percent complete: 79.5%; Average loss: 2.8343
Iteration: 3180; Percent complete: 79.5%; Average loss: 3.1065
Iteration: 3181; Percent complete: 79.5%; Average loss: 2.6818
Iteration: 3182; Percent complete: 79.5%; Average loss: 2.7970
Iteration: 3183; Percent complete: 79.6%; Average loss: 2.9048
Iteration: 3184; Percent complete: 79.6%; Average loss: 2.6201
Iteration: 3185; Percent complete: 79.6%; Average loss: 2.7470
Iteration: 3186; Percent complete: 79.7%; Average loss: 2.8453
Iteration: 3187; Percent complete: 79.7%; Average loss: 2.8316
Iteration: 3188; Percent complete: 79.7%; Average loss: 2.8817
Iteration: 3189; Percent complete: 79.7%; Average loss: 3.0512
Iteration: 3190; Percent complete: 79.8%; Average loss: 2.8424
Iteration: 3191; Percent complete: 79.8%; Average loss: 2.9136
Iteration: 3192; Percent complete: 79.8%; Average loss: 2.8409
Iteration: 3193; Percent complete: 79.8%; Average loss: 2.7443
Iteration: 3194; Percent complete: 79.8%; Average loss: 2.8625
Iteration: 3195; Percent complete: 79.9%; Average loss: 2.6844
Iteration: 3196; Percent complete: 79.9%; Average loss: 2.7509
Iteration: 3197; Percent complete: 79.9%; Average loss: 3.1359
Iteration: 3198; Percent complete: 80.0%; Average loss: 2.7319
Iteration: 3199; Percent complete: 80.0%; Average loss: 2.8034
Iteration: 3200; Percent complete: 80.0%; Average loss: 2.7503
Iteration: 3201; Percent complete: 80.0%; Average loss: 2.6259
Iteration: 3202; Percent complete: 80.0%; Average loss: 2.7397
Iteration: 3203; Percent complete: 80.1%; Average loss: 2.8536
Iteration: 3204; Percent complete: 80.1%; Average loss: 2.8532
Iteration: 3205; Percent complete: 80.1%; Average loss: 2.9292
Iteration: 3206; Percent complete: 80.2%; Average loss: 2.8447
Iteration: 3207; Percent complete: 80.2%; Average loss: 2.7605
Iteration: 3208; Percent complete: 80.2%; Average loss: 2.7404
Iteration: 3209; Percent complete: 80.2%; Average loss: 2.9711
Iteration: 3210; Percent complete: 80.2%; Average loss: 2.7679
Iteration: 3211; Percent complete: 80.3%; Average loss: 2.8184
Iteration: 3212; Percent complete: 80.3%; Average loss: 2.8269
Iteration: 3213; Percent complete: 80.3%; Average loss: 2.7879
Iteration: 3214; Percent complete: 80.3%; Average loss: 2.7970
Iteration: 3215; Percent complete: 80.4%; Average loss: 2.5222
Iteration: 3216; Percent complete: 80.4%; Average loss: 3.0391
Iteration: 3217; Percent complete: 80.4%; Average loss: 2.9628
Iteration: 3218; Percent complete: 80.5%; Average loss: 2.7672
Iteration: 3219; Percent complete: 80.5%; Average loss: 2.8430
Iteration: 3220; Percent complete: 80.5%; Average loss: 3.1084
Iteration: 3221; Percent complete: 80.5%; Average loss: 2.6663
Iteration: 3222; Percent complete: 80.5%; Average loss: 2.7575
Iteration: 3223; Percent complete: 80.6%; Average loss: 2.8445
Iteration: 3224; Percent complete: 80.6%; Average loss: 3.0193
Iteration: 3225; Percent complete: 80.6%; Average loss: 2.8057
Iteration: 3226; Percent complete: 80.7%; Average loss: 2.4829
Iteration: 3227; Percent complete: 80.7%; Average loss: 2.6501
Iteration: 3228; Percent complete: 80.7%; Average loss: 2.7221
Iteration: 3229; Percent complete: 80.7%; Average loss: 3.2253
Iteration: 3230; Percent complete: 80.8%; Average loss: 2.9031
Iteration: 3231; Percent complete: 80.8%; Average loss: 2.9121
Iteration: 3232; Percent complete: 80.8%; Average loss: 3.0071
Iteration: 3233; Percent complete: 80.8%; Average loss: 2.8783
Iteration: 3234; Percent complete: 80.8%; Average loss: 2.9033
Iteration: 3235; Percent complete: 80.9%; Average loss: 2.6073
Iteration: 3236; Percent complete: 80.9%; Average loss: 2.7582
Iteration: 3237; Percent complete: 80.9%; Average loss: 2.6572
Iteration: 3238; Percent complete: 81.0%; Average loss: 2.7837
Iteration: 3239; Percent complete: 81.0%; Average loss: 2.7374
Iteration: 3240; Percent complete: 81.0%; Average loss: 2.6664
Iteration: 3241; Percent complete: 81.0%; Average loss: 2.7566
Iteration: 3242; Percent complete: 81.0%; Average loss: 2.8880
Iteration: 3243; Percent complete: 81.1%; Average loss: 2.9651
Iteration: 3244; Percent complete: 81.1%; Average loss: 2.9606
Iteration: 3245; Percent complete: 81.1%; Average loss: 2.7821
Iteration: 3246; Percent complete: 81.2%; Average loss: 2.7421
Iteration: 3247; Percent complete: 81.2%; Average loss: 2.7829
Iteration: 3248; Percent complete: 81.2%; Average loss: 2.7909
Iteration: 3249; Percent complete: 81.2%; Average loss: 2.9126
Iteration: 3250; Percent complete: 81.2%; Average loss: 2.8909
Iteration: 3251; Percent complete: 81.3%; Average loss: 2.7347
Iteration: 3252; Percent complete: 81.3%; Average loss: 2.9570
Iteration: 3253; Percent complete: 81.3%; Average loss: 2.5940
Iteration: 3254; Percent complete: 81.3%; Average loss: 2.7607
Iteration: 3255; Percent complete: 81.4%; Average loss: 2.8036
Iteration: 3256; Percent complete: 81.4%; Average loss: 3.1309
Iteration: 3257; Percent complete: 81.4%; Average loss: 2.8840
Iteration: 3258; Percent complete: 81.5%; Average loss: 2.8256
Iteration: 3259; Percent complete: 81.5%; Average loss: 2.7394
Iteration: 3260; Percent complete: 81.5%; Average loss: 2.9369
Iteration: 3261; Percent complete: 81.5%; Average loss: 2.7486
Iteration: 3262; Percent complete: 81.5%; Average loss: 2.6339
Iteration: 3263; Percent complete: 81.6%; Average loss: 2.8652
Iteration: 3264; Percent complete: 81.6%; Average loss: 3.0010
Iteration: 3265; Percent complete: 81.6%; Average loss: 2.7453
Iteration: 3266; Percent complete: 81.7%; Average loss: 2.7655
Iteration: 3267; Percent complete: 81.7%; Average loss: 2.6130
Iteration: 3268; Percent complete: 81.7%; Average loss: 2.9497
Iteration: 3269; Percent complete: 81.7%; Average loss: 2.9392
Iteration: 3270; Percent complete: 81.8%; Average loss: 2.7745
Iteration: 3271; Percent complete: 81.8%; Average loss: 2.9085
Iteration: 3272; Percent complete: 81.8%; Average loss: 2.6347
Iteration: 3273; Percent complete: 81.8%; Average loss: 2.9013
Iteration: 3274; Percent complete: 81.8%; Average loss: 2.8479
Iteration: 3275; Percent complete: 81.9%; Average loss: 2.8293
Iteration: 3276; Percent complete: 81.9%; Average loss: 2.8106
Iteration: 3277; Percent complete: 81.9%; Average loss: 2.6585
Iteration: 3278; Percent complete: 82.0%; Average loss: 2.7601
Iteration: 3279; Percent complete: 82.0%; Average loss: 2.8373
Iteration: 3280; Percent complete: 82.0%; Average loss: 2.8702
Iteration: 3281; Percent complete: 82.0%; Average loss: 2.5980
Iteration: 3282; Percent complete: 82.0%; Average loss: 2.7966
Iteration: 3283; Percent complete: 82.1%; Average loss: 2.6616
Iteration: 3284; Percent complete: 82.1%; Average loss: 2.5643
Iteration: 3285; Percent complete: 82.1%; Average loss: 2.8096
Iteration: 3286; Percent complete: 82.2%; Average loss: 2.8246
Iteration: 3287; Percent complete: 82.2%; Average loss: 2.8492
Iteration: 3288; Percent complete: 82.2%; Average loss: 2.8977
Iteration: 3289; Percent complete: 82.2%; Average loss: 2.7819
Iteration: 3290; Percent complete: 82.2%; Average loss: 2.8417
Iteration: 3291; Percent complete: 82.3%; Average loss: 3.0351
Iteration: 3292; Percent complete: 82.3%; Average loss: 2.7099
Iteration: 3293; Percent complete: 82.3%; Average loss: 2.5800
Iteration: 3294; Percent complete: 82.3%; Average loss: 2.5648
Iteration: 3295; Percent complete: 82.4%; Average loss: 2.7389
Iteration: 3296; Percent complete: 82.4%; Average loss: 2.3900
Iteration: 3297; Percent complete: 82.4%; Average loss: 2.9663
Iteration: 3298; Percent complete: 82.5%; Average loss: 2.9820
Iteration: 3299; Percent complete: 82.5%; Average loss: 2.7163
Iteration: 3300; Percent complete: 82.5%; Average loss: 2.7762
Iteration: 3301; Percent complete: 82.5%; Average loss: 2.5622
Iteration: 3302; Percent complete: 82.5%; Average loss: 2.7570
Iteration: 3303; Percent complete: 82.6%; Average loss: 3.0900
Iteration: 3304; Percent complete: 82.6%; Average loss: 2.8268
Iteration: 3305; Percent complete: 82.6%; Average loss: 2.9161
Iteration: 3306; Percent complete: 82.7%; Average loss: 2.5888
Iteration: 3307; Percent complete: 82.7%; Average loss: 2.9106
Iteration: 3308; Percent complete: 82.7%; Average loss: 2.7371
Iteration: 3309; Percent complete: 82.7%; Average loss: 2.9400
Iteration: 3310; Percent complete: 82.8%; Average loss: 2.6475
Iteration: 3311; Percent complete: 82.8%; Average loss: 2.9823
Iteration: 3312; Percent complete: 82.8%; Average loss: 2.6903
Iteration: 3313; Percent complete: 82.8%; Average loss: 2.7856
Iteration: 3314; Percent complete: 82.8%; Average loss: 2.8622
Iteration: 3315; Percent complete: 82.9%; Average loss: 2.6583
Iteration: 3316; Percent complete: 82.9%; Average loss: 3.1210
Iteration: 3317; Percent complete: 82.9%; Average loss: 2.4926
Iteration: 3318; Percent complete: 83.0%; Average loss: 2.9611
Iteration: 3319; Percent complete: 83.0%; Average loss: 2.6596
Iteration: 3320; Percent complete: 83.0%; Average loss: 2.8282
Iteration: 3321; Percent complete: 83.0%; Average loss: 2.7474
Iteration: 3322; Percent complete: 83.0%; Average loss: 2.6570
Iteration: 3323; Percent complete: 83.1%; Average loss: 2.8017
Iteration: 3324; Percent complete: 83.1%; Average loss: 2.7789
Iteration: 3325; Percent complete: 83.1%; Average loss: 2.7794
Iteration: 3326; Percent complete: 83.2%; Average loss: 2.6843
Iteration: 3327; Percent complete: 83.2%; Average loss: 2.6671
Iteration: 3328; Percent complete: 83.2%; Average loss: 2.7615
Iteration: 3329; Percent complete: 83.2%; Average loss: 2.5951
Iteration: 3330; Percent complete: 83.2%; Average loss: 2.6473
Iteration: 3331; Percent complete: 83.3%; Average loss: 3.0182
Iteration: 3332; Percent complete: 83.3%; Average loss: 2.7603
Iteration: 3333; Percent complete: 83.3%; Average loss: 2.8433
Iteration: 3334; Percent complete: 83.4%; Average loss: 2.8519
Iteration: 3335; Percent complete: 83.4%; Average loss: 2.5822
Iteration: 3336; Percent complete: 83.4%; Average loss: 2.8992
Iteration: 3337; Percent complete: 83.4%; Average loss: 2.6114
Iteration: 3338; Percent complete: 83.5%; Average loss: 2.9365
Iteration: 3339; Percent complete: 83.5%; Average loss: 2.8400
Iteration: 3340; Percent complete: 83.5%; Average loss: 3.0923
Iteration: 3341; Percent complete: 83.5%; Average loss: 2.8364
Iteration: 3342; Percent complete: 83.5%; Average loss: 2.9082
Iteration: 3343; Percent complete: 83.6%; Average loss: 3.1124
Iteration: 3344; Percent complete: 83.6%; Average loss: 2.4687
Iteration: 3345; Percent complete: 83.6%; Average loss: 3.1032
Iteration: 3346; Percent complete: 83.7%; Average loss: 2.8944
Iteration: 3347; Percent complete: 83.7%; Average loss: 2.7208
Iteration: 3348; Percent complete: 83.7%; Average loss: 2.7479
Iteration: 3349; Percent complete: 83.7%; Average loss: 2.7633
Iteration: 3350; Percent complete: 83.8%; Average loss: 3.1161
Iteration: 3351; Percent complete: 83.8%; Average loss: 2.8655
Iteration: 3352; Percent complete: 83.8%; Average loss: 2.6768
Iteration: 3353; Percent complete: 83.8%; Average loss: 2.9616
Iteration: 3354; Percent complete: 83.9%; Average loss: 2.9368
Iteration: 3355; Percent complete: 83.9%; Average loss: 2.9777
Iteration: 3356; Percent complete: 83.9%; Average loss: 2.8519
Iteration: 3357; Percent complete: 83.9%; Average loss: 2.6157
Iteration: 3358; Percent complete: 84.0%; Average loss: 2.5867
Iteration: 3359; Percent complete: 84.0%; Average loss: 2.7952
Iteration: 3360; Percent complete: 84.0%; Average loss: 2.8418
Iteration: 3361; Percent complete: 84.0%; Average loss: 2.7389
Iteration: 3362; Percent complete: 84.0%; Average loss: 2.7444
Iteration: 3363; Percent complete: 84.1%; Average loss: 2.8330
Iteration: 3364; Percent complete: 84.1%; Average loss: 2.7059
Iteration: 3365; Percent complete: 84.1%; Average loss: 3.2488
Iteration: 3366; Percent complete: 84.2%; Average loss: 2.7722
Iteration: 3367; Percent complete: 84.2%; Average loss: 2.9876
Iteration: 3368; Percent complete: 84.2%; Average loss: 2.7134
Iteration: 3369; Percent complete: 84.2%; Average loss: 2.6149
Iteration: 3370; Percent complete: 84.2%; Average loss: 2.5967
Iteration: 3371; Percent complete: 84.3%; Average loss: 2.7840
Iteration: 3372; Percent complete: 84.3%; Average loss: 2.5051
Iteration: 3373; Percent complete: 84.3%; Average loss: 2.8546
Iteration: 3374; Percent complete: 84.4%; Average loss: 2.6593
Iteration: 3375; Percent complete: 84.4%; Average loss: 2.7075
Iteration: 3376; Percent complete: 84.4%; Average loss: 2.7992
Iteration: 3377; Percent complete: 84.4%; Average loss: 2.8032
Iteration: 3378; Percent complete: 84.5%; Average loss: 2.6729
Iteration: 3379; Percent complete: 84.5%; Average loss: 2.8538
Iteration: 3380; Percent complete: 84.5%; Average loss: 2.6801
Iteration: 3381; Percent complete: 84.5%; Average loss: 2.7501
Iteration: 3382; Percent complete: 84.5%; Average loss: 2.5455
Iteration: 3383; Percent complete: 84.6%; Average loss: 2.9265
Iteration: 3384; Percent complete: 84.6%; Average loss: 2.7676
Iteration: 3385; Percent complete: 84.6%; Average loss: 2.8265
Iteration: 3386; Percent complete: 84.7%; Average loss: 2.8013
Iteration: 3387; Percent complete: 84.7%; Average loss: 2.7097
Iteration: 3388; Percent complete: 84.7%; Average loss: 2.6454
Iteration: 3389; Percent complete: 84.7%; Average loss: 3.0288
Iteration: 3390; Percent complete: 84.8%; Average loss: 2.6931
Iteration: 3391; Percent complete: 84.8%; Average loss: 2.7591
Iteration: 3392; Percent complete: 84.8%; Average loss: 2.5223
Iteration: 3393; Percent complete: 84.8%; Average loss: 2.8231
Iteration: 3394; Percent complete: 84.9%; Average loss: 2.9269
Iteration: 3395; Percent complete: 84.9%; Average loss: 2.9206
Iteration: 3396; Percent complete: 84.9%; Average loss: 2.5943
Iteration: 3397; Percent complete: 84.9%; Average loss: 2.9856
Iteration: 3398; Percent complete: 85.0%; Average loss: 2.8152
Iteration: 3399; Percent complete: 85.0%; Average loss: 2.8569
Iteration: 3400; Percent complete: 85.0%; Average loss: 2.8653
Iteration: 3401; Percent complete: 85.0%; Average loss: 2.5762
Iteration: 3402; Percent complete: 85.0%; Average loss: 2.8611
Iteration: 3403; Percent complete: 85.1%; Average loss: 2.9151
Iteration: 3404; Percent complete: 85.1%; Average loss: 2.6831
Iteration: 3405; Percent complete: 85.1%; Average loss: 2.5464
Iteration: 3406; Percent complete: 85.2%; Average loss: 2.4389
Iteration: 3407; Percent complete: 85.2%; Average loss: 2.7017
Iteration: 3408; Percent complete: 85.2%; Average loss: 2.8916
Iteration: 3409; Percent complete: 85.2%; Average loss: 2.6243
Iteration: 3410; Percent complete: 85.2%; Average loss: 2.9715
Iteration: 3411; Percent complete: 85.3%; Average loss: 2.6575
Iteration: 3412; Percent complete: 85.3%; Average loss: 2.7271
Iteration: 3413; Percent complete: 85.3%; Average loss: 2.7811
Iteration: 3414; Percent complete: 85.4%; Average loss: 2.8711
Iteration: 3415; Percent complete: 85.4%; Average loss: 2.7382
Iteration: 3416; Percent complete: 85.4%; Average loss: 2.6753
Iteration: 3417; Percent complete: 85.4%; Average loss: 2.9245
Iteration: 3418; Percent complete: 85.5%; Average loss: 2.9068
Iteration: 3419; Percent complete: 85.5%; Average loss: 2.8945
Iteration: 3420; Percent complete: 85.5%; Average loss: 2.9579
Iteration: 3421; Percent complete: 85.5%; Average loss: 2.6743
Iteration: 3422; Percent complete: 85.5%; Average loss: 2.8754
Iteration: 3423; Percent complete: 85.6%; Average loss: 2.7258
Iteration: 3424; Percent complete: 85.6%; Average loss: 2.8114
Iteration: 3425; Percent complete: 85.6%; Average loss: 2.8684
Iteration: 3426; Percent complete: 85.7%; Average loss: 2.5582
Iteration: 3427; Percent complete: 85.7%; Average loss: 2.5577
Iteration: 3428; Percent complete: 85.7%; Average loss: 2.7602
Iteration: 3429; Percent complete: 85.7%; Average loss: 2.7907
Iteration: 3430; Percent complete: 85.8%; Average loss: 2.8138
Iteration: 3431; Percent complete: 85.8%; Average loss: 2.8028
Iteration: 3432; Percent complete: 85.8%; Average loss: 2.6527
Iteration: 3433; Percent complete: 85.8%; Average loss: 3.0052
Iteration: 3434; Percent complete: 85.9%; Average loss: 2.8339
Iteration: 3435; Percent complete: 85.9%; Average loss: 2.7780
Iteration: 3436; Percent complete: 85.9%; Average loss: 2.7962
Iteration: 3437; Percent complete: 85.9%; Average loss: 3.0062
Iteration: 3438; Percent complete: 86.0%; Average loss: 2.5861
Iteration: 3439; Percent complete: 86.0%; Average loss: 2.6195
Iteration: 3440; Percent complete: 86.0%; Average loss: 2.7107
Iteration: 3441; Percent complete: 86.0%; Average loss: 2.8638
Iteration: 3442; Percent complete: 86.1%; Average loss: 2.6820
Iteration: 3443; Percent complete: 86.1%; Average loss: 2.7742
Iteration: 3444; Percent complete: 86.1%; Average loss: 2.6486
Iteration: 3445; Percent complete: 86.1%; Average loss: 2.8849
Iteration: 3446; Percent complete: 86.2%; Average loss: 2.7168
Iteration: 3447; Percent complete: 86.2%; Average loss: 2.7370
Iteration: 3448; Percent complete: 86.2%; Average loss: 2.6092
Iteration: 3449; Percent complete: 86.2%; Average loss: 2.8268
Iteration: 3450; Percent complete: 86.2%; Average loss: 2.7891
Iteration: 3451; Percent complete: 86.3%; Average loss: 2.7275
Iteration: 3452; Percent complete: 86.3%; Average loss: 2.8855
Iteration: 3453; Percent complete: 86.3%; Average loss: 2.8828
Iteration: 3454; Percent complete: 86.4%; Average loss: 2.8487
Iteration: 3455; Percent complete: 86.4%; Average loss: 2.8017
Iteration: 3456; Percent complete: 86.4%; Average loss: 2.7160
Iteration: 3457; Percent complete: 86.4%; Average loss: 2.5888
Iteration: 3458; Percent complete: 86.5%; Average loss: 2.7608
Iteration: 3459; Percent complete: 86.5%; Average loss: 2.7711
Iteration: 3460; Percent complete: 86.5%; Average loss: 2.8694
Iteration: 3461; Percent complete: 86.5%; Average loss: 2.7982
Iteration: 3462; Percent complete: 86.6%; Average loss: 2.6309
Iteration: 3463; Percent complete: 86.6%; Average loss: 2.7172
Iteration: 3464; Percent complete: 86.6%; Average loss: 2.6393
Iteration: 3465; Percent complete: 86.6%; Average loss: 2.6704
Iteration: 3466; Percent complete: 86.7%; Average loss: 2.7239
Iteration: 3467; Percent complete: 86.7%; Average loss: 2.8431
Iteration: 3468; Percent complete: 86.7%; Average loss: 2.9070
Iteration: 3469; Percent complete: 86.7%; Average loss: 2.8643
Iteration: 3470; Percent complete: 86.8%; Average loss: 2.6639
Iteration: 3471; Percent complete: 86.8%; Average loss: 2.9685
Iteration: 3472; Percent complete: 86.8%; Average loss: 2.6478
Iteration: 3473; Percent complete: 86.8%; Average loss: 2.7308
Iteration: 3474; Percent complete: 86.9%; Average loss: 2.7625
Iteration: 3475; Percent complete: 86.9%; Average loss: 2.8132
Iteration: 3476; Percent complete: 86.9%; Average loss: 2.7915
Iteration: 3477; Percent complete: 86.9%; Average loss: 2.7351
Iteration: 3478; Percent complete: 87.0%; Average loss: 2.7293
Iteration: 3479; Percent complete: 87.0%; Average loss: 2.8024
Iteration: 3480; Percent complete: 87.0%; Average loss: 2.6106
Iteration: 3481; Percent complete: 87.0%; Average loss: 2.5873
Iteration: 3482; Percent complete: 87.1%; Average loss: 2.7467
Iteration: 3483; Percent complete: 87.1%; Average loss: 2.7395
Iteration: 3484; Percent complete: 87.1%; Average loss: 2.6399
Iteration: 3485; Percent complete: 87.1%; Average loss: 2.8075
Iteration: 3486; Percent complete: 87.2%; Average loss: 2.8410
Iteration: 3487; Percent complete: 87.2%; Average loss: 2.7671
Iteration: 3488; Percent complete: 87.2%; Average loss: 2.7870
Iteration: 3489; Percent complete: 87.2%; Average loss: 2.7645
Iteration: 3490; Percent complete: 87.2%; Average loss: 2.6548
Iteration: 3491; Percent complete: 87.3%; Average loss: 2.8288
Iteration: 3492; Percent complete: 87.3%; Average loss: 2.9144
Iteration: 3493; Percent complete: 87.3%; Average loss: 2.3364
Iteration: 3494; Percent complete: 87.4%; Average loss: 2.6837
Iteration: 3495; Percent complete: 87.4%; Average loss: 2.7605
Iteration: 3496; Percent complete: 87.4%; Average loss: 2.7401
Iteration: 3497; Percent complete: 87.4%; Average loss: 2.8442
Iteration: 3498; Percent complete: 87.5%; Average loss: 2.7449
Iteration: 3499; Percent complete: 87.5%; Average loss: 3.0453
Iteration: 3500; Percent complete: 87.5%; Average loss: 2.8088
Iteration: 3501; Percent complete: 87.5%; Average loss: 2.8133
Iteration: 3502; Percent complete: 87.5%; Average loss: 2.9017
Iteration: 3503; Percent complete: 87.6%; Average loss: 2.6553
Iteration: 3504; Percent complete: 87.6%; Average loss: 2.7115
Iteration: 3505; Percent complete: 87.6%; Average loss: 2.7031
Iteration: 3506; Percent complete: 87.6%; Average loss: 2.7097
Iteration: 3507; Percent complete: 87.7%; Average loss: 2.8082
Iteration: 3508; Percent complete: 87.7%; Average loss: 2.7648
Iteration: 3509; Percent complete: 87.7%; Average loss: 2.9020
Iteration: 3510; Percent complete: 87.8%; Average loss: 2.9159
Iteration: 3511; Percent complete: 87.8%; Average loss: 2.7307
Iteration: 3512; Percent complete: 87.8%; Average loss: 2.5324
Iteration: 3513; Percent complete: 87.8%; Average loss: 2.8243
Iteration: 3514; Percent complete: 87.8%; Average loss: 3.0248
Iteration: 3515; Percent complete: 87.9%; Average loss: 2.6681
Iteration: 3516; Percent complete: 87.9%; Average loss: 2.8694
Iteration: 3517; Percent complete: 87.9%; Average loss: 2.9154
Iteration: 3518; Percent complete: 87.9%; Average loss: 2.7452
Iteration: 3519; Percent complete: 88.0%; Average loss: 2.5520
Iteration: 3520; Percent complete: 88.0%; Average loss: 2.7017
Iteration: 3521; Percent complete: 88.0%; Average loss: 2.5715
Iteration: 3522; Percent complete: 88.0%; Average loss: 2.5450
Iteration: 3523; Percent complete: 88.1%; Average loss: 2.6110
Iteration: 3524; Percent complete: 88.1%; Average loss: 2.7275
Iteration: 3525; Percent complete: 88.1%; Average loss: 2.6866
Iteration: 3526; Percent complete: 88.1%; Average loss: 2.8675
Iteration: 3527; Percent complete: 88.2%; Average loss: 2.5217
Iteration: 3528; Percent complete: 88.2%; Average loss: 2.8751
Iteration: 3529; Percent complete: 88.2%; Average loss: 2.6755
Iteration: 3530; Percent complete: 88.2%; Average loss: 2.6328
Iteration: 3531; Percent complete: 88.3%; Average loss: 3.0135
Iteration: 3532; Percent complete: 88.3%; Average loss: 2.7758
Iteration: 3533; Percent complete: 88.3%; Average loss: 2.5113
Iteration: 3534; Percent complete: 88.3%; Average loss: 2.8251
Iteration: 3535; Percent complete: 88.4%; Average loss: 2.7585
Iteration: 3536; Percent complete: 88.4%; Average loss: 2.8662
Iteration: 3537; Percent complete: 88.4%; Average loss: 2.8418
Iteration: 3538; Percent complete: 88.4%; Average loss: 2.5833
Iteration: 3539; Percent complete: 88.5%; Average loss: 2.3937
Iteration: 3540; Percent complete: 88.5%; Average loss: 2.8374
Iteration: 3541; Percent complete: 88.5%; Average loss: 2.6900
Iteration: 3542; Percent complete: 88.5%; Average loss: 2.8970
Iteration: 3543; Percent complete: 88.6%; Average loss: 2.6560
Iteration: 3544; Percent complete: 88.6%; Average loss: 2.5039
Iteration: 3545; Percent complete: 88.6%; Average loss: 2.6877
Iteration: 3546; Percent complete: 88.6%; Average loss: 2.8122
Iteration: 3547; Percent complete: 88.7%; Average loss: 2.9127
Iteration: 3548; Percent complete: 88.7%; Average loss: 3.0432
Iteration: 3549; Percent complete: 88.7%; Average loss: 2.7891
Iteration: 3550; Percent complete: 88.8%; Average loss: 2.6640
Iteration: 3551; Percent complete: 88.8%; Average loss: 2.7200
Iteration: 3552; Percent complete: 88.8%; Average loss: 2.7101
Iteration: 3553; Percent complete: 88.8%; Average loss: 2.6575
Iteration: 3554; Percent complete: 88.8%; Average loss: 2.6857
Iteration: 3555; Percent complete: 88.9%; Average loss: 2.8301
Iteration: 3556; Percent complete: 88.9%; Average loss: 2.8435
Iteration: 3557; Percent complete: 88.9%; Average loss: 2.7465
Iteration: 3558; Percent complete: 88.9%; Average loss: 2.6502
Iteration: 3559; Percent complete: 89.0%; Average loss: 2.6391
Iteration: 3560; Percent complete: 89.0%; Average loss: 2.6562
Iteration: 3561; Percent complete: 89.0%; Average loss: 2.7555
Iteration: 3562; Percent complete: 89.0%; Average loss: 2.7504
Iteration: 3563; Percent complete: 89.1%; Average loss: 2.7613
Iteration: 3564; Percent complete: 89.1%; Average loss: 2.5432
Iteration: 3565; Percent complete: 89.1%; Average loss: 2.9861
Iteration: 3566; Percent complete: 89.1%; Average loss: 2.9432
Iteration: 3567; Percent complete: 89.2%; Average loss: 2.5247
Iteration: 3568; Percent complete: 89.2%; Average loss: 2.7517
Iteration: 3569; Percent complete: 89.2%; Average loss: 2.6685
Iteration: 3570; Percent complete: 89.2%; Average loss: 2.8226
Iteration: 3571; Percent complete: 89.3%; Average loss: 2.9532
Iteration: 3572; Percent complete: 89.3%; Average loss: 2.3881
Iteration: 3573; Percent complete: 89.3%; Average loss: 2.4857
Iteration: 3574; Percent complete: 89.3%; Average loss: 2.6022
Iteration: 3575; Percent complete: 89.4%; Average loss: 2.7432
Iteration: 3576; Percent complete: 89.4%; Average loss: 2.7673
Iteration: 3577; Percent complete: 89.4%; Average loss: 2.8125
Iteration: 3578; Percent complete: 89.5%; Average loss: 2.8576
Iteration: 3579; Percent complete: 89.5%; Average loss: 2.8959
Iteration: 3580; Percent complete: 89.5%; Average loss: 2.8516
Iteration: 3581; Percent complete: 89.5%; Average loss: 2.7656
Iteration: 3582; Percent complete: 89.5%; Average loss: 2.9752
Iteration: 3583; Percent complete: 89.6%; Average loss: 2.7649
Iteration: 3584; Percent complete: 89.6%; Average loss: 2.6239
Iteration: 3585; Percent complete: 89.6%; Average loss: 2.5755
Iteration: 3586; Percent complete: 89.6%; Average loss: 2.5376
Iteration: 3587; Percent complete: 89.7%; Average loss: 2.6902
Iteration: 3588; Percent complete: 89.7%; Average loss: 2.6389
Iteration: 3589; Percent complete: 89.7%; Average loss: 2.8125
Iteration: 3590; Percent complete: 89.8%; Average loss: 2.7183
Iteration: 3591; Percent complete: 89.8%; Average loss: 2.4431
Iteration: 3592; Percent complete: 89.8%; Average loss: 2.9161
Iteration: 3593; Percent complete: 89.8%; Average loss: 2.4917
Iteration: 3594; Percent complete: 89.8%; Average loss: 2.6076
Iteration: 3595; Percent complete: 89.9%; Average loss: 2.7920
Iteration: 3596; Percent complete: 89.9%; Average loss: 2.8479
Iteration: 3597; Percent complete: 89.9%; Average loss: 2.5676
Iteration: 3598; Percent complete: 90.0%; Average loss: 2.7844
Iteration: 3599; Percent complete: 90.0%; Average loss: 2.8628
Iteration: 3600; Percent complete: 90.0%; Average loss: 2.8524
Iteration: 3601; Percent complete: 90.0%; Average loss: 2.8027
Iteration: 3602; Percent complete: 90.0%; Average loss: 2.6502
Iteration: 3603; Percent complete: 90.1%; Average loss: 2.6690
Iteration: 3604; Percent complete: 90.1%; Average loss: 2.7488
Iteration: 3605; Percent complete: 90.1%; Average loss: 2.8264
Iteration: 3606; Percent complete: 90.1%; Average loss: 2.7094
Iteration: 3607; Percent complete: 90.2%; Average loss: 2.4716
Iteration: 3608; Percent complete: 90.2%; Average loss: 2.6736
Iteration: 3609; Percent complete: 90.2%; Average loss: 2.9528
Iteration: 3610; Percent complete: 90.2%; Average loss: 2.7602
Iteration: 3611; Percent complete: 90.3%; Average loss: 2.5196
Iteration: 3612; Percent complete: 90.3%; Average loss: 2.7873
Iteration: 3613; Percent complete: 90.3%; Average loss: 2.7961
Iteration: 3614; Percent complete: 90.3%; Average loss: 2.8544
Iteration: 3615; Percent complete: 90.4%; Average loss: 2.4318
Iteration: 3616; Percent complete: 90.4%; Average loss: 2.8205
Iteration: 3617; Percent complete: 90.4%; Average loss: 2.6904
Iteration: 3618; Percent complete: 90.5%; Average loss: 2.7827
Iteration: 3619; Percent complete: 90.5%; Average loss: 2.7267
Iteration: 3620; Percent complete: 90.5%; Average loss: 2.6108
Iteration: 3621; Percent complete: 90.5%; Average loss: 2.6739
Iteration: 3622; Percent complete: 90.5%; Average loss: 2.6754
Iteration: 3623; Percent complete: 90.6%; Average loss: 2.7678
Iteration: 3624; Percent complete: 90.6%; Average loss: 2.9137
Iteration: 3625; Percent complete: 90.6%; Average loss: 2.7931
Iteration: 3626; Percent complete: 90.6%; Average loss: 2.6625
Iteration: 3627; Percent complete: 90.7%; Average loss: 2.3956
Iteration: 3628; Percent complete: 90.7%; Average loss: 2.6063
Iteration: 3629; Percent complete: 90.7%; Average loss: 2.5456
Iteration: 3630; Percent complete: 90.8%; Average loss: 2.6831
Iteration: 3631; Percent complete: 90.8%; Average loss: 2.8099
Iteration: 3632; Percent complete: 90.8%; Average loss: 2.6397
Iteration: 3633; Percent complete: 90.8%; Average loss: 2.9179
Iteration: 3634; Percent complete: 90.8%; Average loss: 2.6501
Iteration: 3635; Percent complete: 90.9%; Average loss: 2.7064
Iteration: 3636; Percent complete: 90.9%; Average loss: 2.7360
Iteration: 3637; Percent complete: 90.9%; Average loss: 2.7460
Iteration: 3638; Percent complete: 91.0%; Average loss: 2.7674
Iteration: 3639; Percent complete: 91.0%; Average loss: 2.5742
Iteration: 3640; Percent complete: 91.0%; Average loss: 2.6286
Iteration: 3641; Percent complete: 91.0%; Average loss: 2.6342
Iteration: 3642; Percent complete: 91.0%; Average loss: 2.7379
Iteration: 3643; Percent complete: 91.1%; Average loss: 2.5131
Iteration: 3644; Percent complete: 91.1%; Average loss: 2.7721
Iteration: 3645; Percent complete: 91.1%; Average loss: 2.6116
Iteration: 3646; Percent complete: 91.1%; Average loss: 2.5352
Iteration: 3647; Percent complete: 91.2%; Average loss: 2.4961
Iteration: 3648; Percent complete: 91.2%; Average loss: 2.6919
Iteration: 3649; Percent complete: 91.2%; Average loss: 2.6343
Iteration: 3650; Percent complete: 91.2%; Average loss: 2.8184
Iteration: 3651; Percent complete: 91.3%; Average loss: 2.7556
Iteration: 3652; Percent complete: 91.3%; Average loss: 2.6885
Iteration: 3653; Percent complete: 91.3%; Average loss: 2.8134
Iteration: 3654; Percent complete: 91.3%; Average loss: 2.7120
Iteration: 3655; Percent complete: 91.4%; Average loss: 2.8009
Iteration: 3656; Percent complete: 91.4%; Average loss: 2.7240
Iteration: 3657; Percent complete: 91.4%; Average loss: 2.5202
Iteration: 3658; Percent complete: 91.5%; Average loss: 2.8213
Iteration: 3659; Percent complete: 91.5%; Average loss: 2.7181
Iteration: 3660; Percent complete: 91.5%; Average loss: 2.7013
Iteration: 3661; Percent complete: 91.5%; Average loss: 2.7051
Iteration: 3662; Percent complete: 91.5%; Average loss: 2.7462
Iteration: 3663; Percent complete: 91.6%; Average loss: 2.7045
Iteration: 3664; Percent complete: 91.6%; Average loss: 2.6890
Iteration: 3665; Percent complete: 91.6%; Average loss: 2.6965
Iteration: 3666; Percent complete: 91.6%; Average loss: 2.6509
Iteration: 3667; Percent complete: 91.7%; Average loss: 2.5670
Iteration: 3668; Percent complete: 91.7%; Average loss: 2.5609
Iteration: 3669; Percent complete: 91.7%; Average loss: 2.4666
Iteration: 3670; Percent complete: 91.8%; Average loss: 3.0051
Iteration: 3671; Percent complete: 91.8%; Average loss: 2.5902
Iteration: 3672; Percent complete: 91.8%; Average loss: 2.6471
Iteration: 3673; Percent complete: 91.8%; Average loss: 2.6139
Iteration: 3674; Percent complete: 91.8%; Average loss: 3.0163
Iteration: 3675; Percent complete: 91.9%; Average loss: 2.7431
Iteration: 3676; Percent complete: 91.9%; Average loss: 2.3858
Iteration: 3677; Percent complete: 91.9%; Average loss: 2.5922
Iteration: 3678; Percent complete: 92.0%; Average loss: 2.7085
Iteration: 3679; Percent complete: 92.0%; Average loss: 2.7521
Iteration: 3680; Percent complete: 92.0%; Average loss: 2.7343
Iteration: 3681; Percent complete: 92.0%; Average loss: 2.7844
Iteration: 3682; Percent complete: 92.0%; Average loss: 2.9289
Iteration: 3683; Percent complete: 92.1%; Average loss: 2.5252
Iteration: 3684; Percent complete: 92.1%; Average loss: 2.6484
Iteration: 3685; Percent complete: 92.1%; Average loss: 2.6098
Iteration: 3686; Percent complete: 92.2%; Average loss: 2.5693
Iteration: 3687; Percent complete: 92.2%; Average loss: 2.5565
Iteration: 3688; Percent complete: 92.2%; Average loss: 2.6839
Iteration: 3689; Percent complete: 92.2%; Average loss: 2.6870
Iteration: 3690; Percent complete: 92.2%; Average loss: 2.5696
Iteration: 3691; Percent complete: 92.3%; Average loss: 2.5904
Iteration: 3692; Percent complete: 92.3%; Average loss: 2.6813
Iteration: 3693; Percent complete: 92.3%; Average loss: 2.5369
Iteration: 3694; Percent complete: 92.3%; Average loss: 2.8034
Iteration: 3695; Percent complete: 92.4%; Average loss: 2.6200
Iteration: 3696; Percent complete: 92.4%; Average loss: 2.6911
Iteration: 3697; Percent complete: 92.4%; Average loss: 2.5529
Iteration: 3698; Percent complete: 92.5%; Average loss: 2.7339
Iteration: 3699; Percent complete: 92.5%; Average loss: 2.7104
Iteration: 3700; Percent complete: 92.5%; Average loss: 2.8514
Iteration: 3701; Percent complete: 92.5%; Average loss: 2.7046
Iteration: 3702; Percent complete: 92.5%; Average loss: 2.7672
Iteration: 3703; Percent complete: 92.6%; Average loss: 2.5669
Iteration: 3704; Percent complete: 92.6%; Average loss: 2.7008
Iteration: 3705; Percent complete: 92.6%; Average loss: 2.5706
Iteration: 3706; Percent complete: 92.7%; Average loss: 2.6920
Iteration: 3707; Percent complete: 92.7%; Average loss: 2.6478
Iteration: 3708; Percent complete: 92.7%; Average loss: 2.6709
Iteration: 3709; Percent complete: 92.7%; Average loss: 2.5922
Iteration: 3710; Percent complete: 92.8%; Average loss: 2.8878
Iteration: 3711; Percent complete: 92.8%; Average loss: 2.8525
Iteration: 3712; Percent complete: 92.8%; Average loss: 2.7885
Iteration: 3713; Percent complete: 92.8%; Average loss: 2.8135
Iteration: 3714; Percent complete: 92.8%; Average loss: 2.9270
Iteration: 3715; Percent complete: 92.9%; Average loss: 2.7605
Iteration: 3716; Percent complete: 92.9%; Average loss: 2.7423
Iteration: 3717; Percent complete: 92.9%; Average loss: 2.7485
Iteration: 3718; Percent complete: 93.0%; Average loss: 2.7144
Iteration: 3719; Percent complete: 93.0%; Average loss: 2.7033
Iteration: 3720; Percent complete: 93.0%; Average loss: 2.7776
Iteration: 3721; Percent complete: 93.0%; Average loss: 2.5552
Iteration: 3722; Percent complete: 93.0%; Average loss: 2.6911
Iteration: 3723; Percent complete: 93.1%; Average loss: 2.6521
Iteration: 3724; Percent complete: 93.1%; Average loss: 2.5941
Iteration: 3725; Percent complete: 93.1%; Average loss: 2.7617
Iteration: 3726; Percent complete: 93.2%; Average loss: 2.7583
Iteration: 3727; Percent complete: 93.2%; Average loss: 2.9078
Iteration: 3728; Percent complete: 93.2%; Average loss: 2.6658
Iteration: 3729; Percent complete: 93.2%; Average loss: 2.6812
Iteration: 3730; Percent complete: 93.2%; Average loss: 2.8265
Iteration: 3731; Percent complete: 93.3%; Average loss: 2.6691
Iteration: 3732; Percent complete: 93.3%; Average loss: 2.6006
Iteration: 3733; Percent complete: 93.3%; Average loss: 2.6060
Iteration: 3734; Percent complete: 93.3%; Average loss: 2.8122
Iteration: 3735; Percent complete: 93.4%; Average loss: 2.5444
Iteration: 3736; Percent complete: 93.4%; Average loss: 2.7790
Iteration: 3737; Percent complete: 93.4%; Average loss: 2.5792
Iteration: 3738; Percent complete: 93.5%; Average loss: 2.8911
Iteration: 3739; Percent complete: 93.5%; Average loss: 2.4808
Iteration: 3740; Percent complete: 93.5%; Average loss: 2.9465
Iteration: 3741; Percent complete: 93.5%; Average loss: 2.7526
Iteration: 3742; Percent complete: 93.5%; Average loss: 2.7780
Iteration: 3743; Percent complete: 93.6%; Average loss: 2.4650
Iteration: 3744; Percent complete: 93.6%; Average loss: 2.6916
Iteration: 3745; Percent complete: 93.6%; Average loss: 2.8182
Iteration: 3746; Percent complete: 93.7%; Average loss: 2.6588
Iteration: 3747; Percent complete: 93.7%; Average loss: 2.7311
Iteration: 3748; Percent complete: 93.7%; Average loss: 2.8897
Iteration: 3749; Percent complete: 93.7%; Average loss: 2.8580
Iteration: 3750; Percent complete: 93.8%; Average loss: 2.7728
Iteration: 3751; Percent complete: 93.8%; Average loss: 2.8349
Iteration: 3752; Percent complete: 93.8%; Average loss: 2.6563
Iteration: 3753; Percent complete: 93.8%; Average loss: 2.5910
Iteration: 3754; Percent complete: 93.8%; Average loss: 2.7431
Iteration: 3755; Percent complete: 93.9%; Average loss: 2.6901
Iteration: 3756; Percent complete: 93.9%; Average loss: 2.8069
Iteration: 3757; Percent complete: 93.9%; Average loss: 2.6267
Iteration: 3758; Percent complete: 94.0%; Average loss: 2.6660
Iteration: 3759; Percent complete: 94.0%; Average loss: 2.6515
Iteration: 3760; Percent complete: 94.0%; Average loss: 2.6059
Iteration: 3761; Percent complete: 94.0%; Average loss: 2.7225
Iteration: 3762; Percent complete: 94.0%; Average loss: 2.7086
Iteration: 3763; Percent complete: 94.1%; Average loss: 2.6789
Iteration: 3764; Percent complete: 94.1%; Average loss: 2.7931
Iteration: 3765; Percent complete: 94.1%; Average loss: 2.7002
Iteration: 3766; Percent complete: 94.2%; Average loss: 2.6974
Iteration: 3767; Percent complete: 94.2%; Average loss: 2.4043
Iteration: 3768; Percent complete: 94.2%; Average loss: 2.4635
Iteration: 3769; Percent complete: 94.2%; Average loss: 2.7203
Iteration: 3770; Percent complete: 94.2%; Average loss: 2.6677
Iteration: 3771; Percent complete: 94.3%; Average loss: 2.8690
Iteration: 3772; Percent complete: 94.3%; Average loss: 2.4983
Iteration: 3773; Percent complete: 94.3%; Average loss: 2.6789
Iteration: 3774; Percent complete: 94.3%; Average loss: 2.6069
Iteration: 3775; Percent complete: 94.4%; Average loss: 2.8418
Iteration: 3776; Percent complete: 94.4%; Average loss: 2.5813
Iteration: 3777; Percent complete: 94.4%; Average loss: 2.9176
Iteration: 3778; Percent complete: 94.5%; Average loss: 2.7786
Iteration: 3779; Percent complete: 94.5%; Average loss: 2.7252
Iteration: 3780; Percent complete: 94.5%; Average loss: 2.3888
Iteration: 3781; Percent complete: 94.5%; Average loss: 2.7621
Iteration: 3782; Percent complete: 94.5%; Average loss: 2.5657
Iteration: 3783; Percent complete: 94.6%; Average loss: 2.7861
Iteration: 3784; Percent complete: 94.6%; Average loss: 2.5757
Iteration: 3785; Percent complete: 94.6%; Average loss: 2.6414
Iteration: 3786; Percent complete: 94.7%; Average loss: 2.4935
Iteration: 3787; Percent complete: 94.7%; Average loss: 2.8319
Iteration: 3788; Percent complete: 94.7%; Average loss: 2.8285
Iteration: 3789; Percent complete: 94.7%; Average loss: 2.6591
Iteration: 3790; Percent complete: 94.8%; Average loss: 2.4309
Iteration: 3791; Percent complete: 94.8%; Average loss: 2.8431
Iteration: 3792; Percent complete: 94.8%; Average loss: 2.6602
Iteration: 3793; Percent complete: 94.8%; Average loss: 2.6834
Iteration: 3794; Percent complete: 94.8%; Average loss: 2.5014
Iteration: 3795; Percent complete: 94.9%; Average loss: 2.7650
Iteration: 3796; Percent complete: 94.9%; Average loss: 2.5647
Iteration: 3797; Percent complete: 94.9%; Average loss: 2.7749
Iteration: 3798; Percent complete: 95.0%; Average loss: 2.7193
Iteration: 3799; Percent complete: 95.0%; Average loss: 2.6379
Iteration: 3800; Percent complete: 95.0%; Average loss: 2.7228
Iteration: 3801; Percent complete: 95.0%; Average loss: 2.6888
Iteration: 3802; Percent complete: 95.0%; Average loss: 2.5088
Iteration: 3803; Percent complete: 95.1%; Average loss: 2.4781
Iteration: 3804; Percent complete: 95.1%; Average loss: 2.8266
Iteration: 3805; Percent complete: 95.1%; Average loss: 2.6790
Iteration: 3806; Percent complete: 95.2%; Average loss: 2.7080
Iteration: 3807; Percent complete: 95.2%; Average loss: 2.7774
Iteration: 3808; Percent complete: 95.2%; Average loss: 2.5300
Iteration: 3809; Percent complete: 95.2%; Average loss: 2.8383
Iteration: 3810; Percent complete: 95.2%; Average loss: 2.6299
Iteration: 3811; Percent complete: 95.3%; Average loss: 2.6951
Iteration: 3812; Percent complete: 95.3%; Average loss: 2.8878
Iteration: 3813; Percent complete: 95.3%; Average loss: 2.5801
Iteration: 3814; Percent complete: 95.3%; Average loss: 2.6540
Iteration: 3815; Percent complete: 95.4%; Average loss: 2.5268
Iteration: 3816; Percent complete: 95.4%; Average loss: 2.7003
Iteration: 3817; Percent complete: 95.4%; Average loss: 2.4119
Iteration: 3818; Percent complete: 95.5%; Average loss: 2.7983
Iteration: 3819; Percent complete: 95.5%; Average loss: 2.7258
Iteration: 3820; Percent complete: 95.5%; Average loss: 2.5074
Iteration: 3821; Percent complete: 95.5%; Average loss: 2.7863
Iteration: 3822; Percent complete: 95.5%; Average loss: 2.6625
Iteration: 3823; Percent complete: 95.6%; Average loss: 2.4638
Iteration: 3824; Percent complete: 95.6%; Average loss: 2.5762
Iteration: 3825; Percent complete: 95.6%; Average loss: 2.6895
Iteration: 3826; Percent complete: 95.7%; Average loss: 2.5711
Iteration: 3827; Percent complete: 95.7%; Average loss: 2.6745
Iteration: 3828; Percent complete: 95.7%; Average loss: 2.6889
Iteration: 3829; Percent complete: 95.7%; Average loss: 2.4810
Iteration: 3830; Percent complete: 95.8%; Average loss: 2.5762
Iteration: 3831; Percent complete: 95.8%; Average loss: 2.9014
Iteration: 3832; Percent complete: 95.8%; Average loss: 2.7683
Iteration: 3833; Percent complete: 95.8%; Average loss: 2.6449
Iteration: 3834; Percent complete: 95.9%; Average loss: 2.8322
Iteration: 3835; Percent complete: 95.9%; Average loss: 2.8180
Iteration: 3836; Percent complete: 95.9%; Average loss: 2.6499
Iteration: 3837; Percent complete: 95.9%; Average loss: 2.6304
Iteration: 3838; Percent complete: 96.0%; Average loss: 2.7089
Iteration: 3839; Percent complete: 96.0%; Average loss: 2.8181
Iteration: 3840; Percent complete: 96.0%; Average loss: 2.4089
Iteration: 3841; Percent complete: 96.0%; Average loss: 2.7750
Iteration: 3842; Percent complete: 96.0%; Average loss: 2.6003
Iteration: 3843; Percent complete: 96.1%; Average loss: 2.7639
Iteration: 3844; Percent complete: 96.1%; Average loss: 2.7088
Iteration: 3845; Percent complete: 96.1%; Average loss: 2.6615
Iteration: 3846; Percent complete: 96.2%; Average loss: 2.6675
Iteration: 3847; Percent complete: 96.2%; Average loss: 2.7065
Iteration: 3848; Percent complete: 96.2%; Average loss: 2.7448
Iteration: 3849; Percent complete: 96.2%; Average loss: 2.7147
Iteration: 3850; Percent complete: 96.2%; Average loss: 2.5167
Iteration: 3851; Percent complete: 96.3%; Average loss: 2.7725
Iteration: 3852; Percent complete: 96.3%; Average loss: 2.6011
Iteration: 3853; Percent complete: 96.3%; Average loss: 2.6946
Iteration: 3854; Percent complete: 96.4%; Average loss: 2.8852
Iteration: 3855; Percent complete: 96.4%; Average loss: 2.7518
Iteration: 3856; Percent complete: 96.4%; Average loss: 2.8218
Iteration: 3857; Percent complete: 96.4%; Average loss: 2.6528
Iteration: 3858; Percent complete: 96.5%; Average loss: 2.2359
Iteration: 3859; Percent complete: 96.5%; Average loss: 2.7618
Iteration: 3860; Percent complete: 96.5%; Average loss: 2.7018
Iteration: 3861; Percent complete: 96.5%; Average loss: 2.6540
Iteration: 3862; Percent complete: 96.5%; Average loss: 2.6371
Iteration: 3863; Percent complete: 96.6%; Average loss: 2.4137
Iteration: 3864; Percent complete: 96.6%; Average loss: 2.5862
Iteration: 3865; Percent complete: 96.6%; Average loss: 2.6209
Iteration: 3866; Percent complete: 96.7%; Average loss: 2.8093
Iteration: 3867; Percent complete: 96.7%; Average loss: 2.5733
Iteration: 3868; Percent complete: 96.7%; Average loss: 2.6284
Iteration: 3869; Percent complete: 96.7%; Average loss: 2.5564
Iteration: 3870; Percent complete: 96.8%; Average loss: 2.6335
Iteration: 3871; Percent complete: 96.8%; Average loss: 2.6114
Iteration: 3872; Percent complete: 96.8%; Average loss: 2.6847
Iteration: 3873; Percent complete: 96.8%; Average loss: 2.6302
Iteration: 3874; Percent complete: 96.9%; Average loss: 2.6415
Iteration: 3875; Percent complete: 96.9%; Average loss: 2.6186
Iteration: 3876; Percent complete: 96.9%; Average loss: 2.5566
Iteration: 3877; Percent complete: 96.9%; Average loss: 2.5641
Iteration: 3878; Percent complete: 97.0%; Average loss: 2.9389
Iteration: 3879; Percent complete: 97.0%; Average loss: 2.5559
Iteration: 3880; Percent complete: 97.0%; Average loss: 2.5949
Iteration: 3881; Percent complete: 97.0%; Average loss: 2.7277
Iteration: 3882; Percent complete: 97.0%; Average loss: 2.6388
Iteration: 3883; Percent complete: 97.1%; Average loss: 2.7204
Iteration: 3884; Percent complete: 97.1%; Average loss: 2.6936
Iteration: 3885; Percent complete: 97.1%; Average loss: 2.5500
Iteration: 3886; Percent complete: 97.2%; Average loss: 2.5803
Iteration: 3887; Percent complete: 97.2%; Average loss: 2.6271
Iteration: 3888; Percent complete: 97.2%; Average loss: 2.5951
Iteration: 3889; Percent complete: 97.2%; Average loss: 2.4191
Iteration: 3890; Percent complete: 97.2%; Average loss: 2.3665
Iteration: 3891; Percent complete: 97.3%; Average loss: 2.7640
Iteration: 3892; Percent complete: 97.3%; Average loss: 2.8572
Iteration: 3893; Percent complete: 97.3%; Average loss: 2.6333
Iteration: 3894; Percent complete: 97.4%; Average loss: 2.8319
Iteration: 3895; Percent complete: 97.4%; Average loss: 2.6734
Iteration: 3896; Percent complete: 97.4%; Average loss: 2.6259
Iteration: 3897; Percent complete: 97.4%; Average loss: 2.7083
Iteration: 3898; Percent complete: 97.5%; Average loss: 2.7460
Iteration: 3899; Percent complete: 97.5%; Average loss: 2.7239
Iteration: 3900; Percent complete: 97.5%; Average loss: 2.6245
Iteration: 3901; Percent complete: 97.5%; Average loss: 2.9027
Iteration: 3902; Percent complete: 97.5%; Average loss: 2.4674
Iteration: 3903; Percent complete: 97.6%; Average loss: 2.6627
Iteration: 3904; Percent complete: 97.6%; Average loss: 2.4876
Iteration: 3905; Percent complete: 97.6%; Average loss: 2.7621
Iteration: 3906; Percent complete: 97.7%; Average loss: 2.7965
Iteration: 3907; Percent complete: 97.7%; Average loss: 2.5371
Iteration: 3908; Percent complete: 97.7%; Average loss: 2.5516
Iteration: 3909; Percent complete: 97.7%; Average loss: 2.4596
Iteration: 3910; Percent complete: 97.8%; Average loss: 2.4602
Iteration: 3911; Percent complete: 97.8%; Average loss: 2.4098
Iteration: 3912; Percent complete: 97.8%; Average loss: 2.6966
Iteration: 3913; Percent complete: 97.8%; Average loss: 2.6590
Iteration: 3914; Percent complete: 97.9%; Average loss: 2.6947
Iteration: 3915; Percent complete: 97.9%; Average loss: 2.8635
Iteration: 3916; Percent complete: 97.9%; Average loss: 2.7221
Iteration: 3917; Percent complete: 97.9%; Average loss: 2.7478
Iteration: 3918; Percent complete: 98.0%; Average loss: 2.4599
Iteration: 3919; Percent complete: 98.0%; Average loss: 2.5365
Iteration: 3920; Percent complete: 98.0%; Average loss: 2.6077
Iteration: 3921; Percent complete: 98.0%; Average loss: 2.5156
Iteration: 3922; Percent complete: 98.0%; Average loss: 2.6820
Iteration: 3923; Percent complete: 98.1%; Average loss: 2.9707
Iteration: 3924; Percent complete: 98.1%; Average loss: 2.7237
Iteration: 3925; Percent complete: 98.1%; Average loss: 2.7227
Iteration: 3926; Percent complete: 98.2%; Average loss: 2.7043
Iteration: 3927; Percent complete: 98.2%; Average loss: 2.6790
Iteration: 3928; Percent complete: 98.2%; Average loss: 2.4915
Iteration: 3929; Percent complete: 98.2%; Average loss: 2.6707
Iteration: 3930; Percent complete: 98.2%; Average loss: 2.9010
Iteration: 3931; Percent complete: 98.3%; Average loss: 2.7449
Iteration: 3932; Percent complete: 98.3%; Average loss: 2.7910
Iteration: 3933; Percent complete: 98.3%; Average loss: 2.6825
Iteration: 3934; Percent complete: 98.4%; Average loss: 2.7469
Iteration: 3935; Percent complete: 98.4%; Average loss: 2.6510
Iteration: 3936; Percent complete: 98.4%; Average loss: 2.8094
Iteration: 3937; Percent complete: 98.4%; Average loss: 2.4853
Iteration: 3938; Percent complete: 98.5%; Average loss: 2.5768
Iteration: 3939; Percent complete: 98.5%; Average loss: 2.4804
Iteration: 3940; Percent complete: 98.5%; Average loss: 2.5995
Iteration: 3941; Percent complete: 98.5%; Average loss: 2.6931
Iteration: 3942; Percent complete: 98.6%; Average loss: 2.8542
Iteration: 3943; Percent complete: 98.6%; Average loss: 2.5319
Iteration: 3944; Percent complete: 98.6%; Average loss: 2.7523
Iteration: 3945; Percent complete: 98.6%; Average loss: 2.5202
Iteration: 3946; Percent complete: 98.7%; Average loss: 2.5198
Iteration: 3947; Percent complete: 98.7%; Average loss: 2.5545
Iteration: 3948; Percent complete: 98.7%; Average loss: 2.6065
Iteration: 3949; Percent complete: 98.7%; Average loss: 2.4935
Iteration: 3950; Percent complete: 98.8%; Average loss: 2.9162
Iteration: 3951; Percent complete: 98.8%; Average loss: 2.5903
Iteration: 3952; Percent complete: 98.8%; Average loss: 2.9641
Iteration: 3953; Percent complete: 98.8%; Average loss: 2.3266
Iteration: 3954; Percent complete: 98.9%; Average loss: 2.4152
Iteration: 3955; Percent complete: 98.9%; Average loss: 2.5981
Iteration: 3956; Percent complete: 98.9%; Average loss: 2.6306
Iteration: 3957; Percent complete: 98.9%; Average loss: 2.9396
Iteration: 3958; Percent complete: 99.0%; Average loss: 2.6039
Iteration: 3959; Percent complete: 99.0%; Average loss: 2.4050
Iteration: 3960; Percent complete: 99.0%; Average loss: 2.7904
Iteration: 3961; Percent complete: 99.0%; Average loss: 2.4928
Iteration: 3962; Percent complete: 99.1%; Average loss: 2.7148
Iteration: 3963; Percent complete: 99.1%; Average loss: 2.6888
Iteration: 3964; Percent complete: 99.1%; Average loss: 2.4986
Iteration: 3965; Percent complete: 99.1%; Average loss: 2.6423
Iteration: 3966; Percent complete: 99.2%; Average loss: 2.7480
Iteration: 3967; Percent complete: 99.2%; Average loss: 2.6646
Iteration: 3968; Percent complete: 99.2%; Average loss: 2.5776
Iteration: 3969; Percent complete: 99.2%; Average loss: 2.5013
Iteration: 3970; Percent complete: 99.2%; Average loss: 2.9720
Iteration: 3971; Percent complete: 99.3%; Average loss: 2.7475
Iteration: 3972; Percent complete: 99.3%; Average loss: 2.7526
Iteration: 3973; Percent complete: 99.3%; Average loss: 2.5612
Iteration: 3974; Percent complete: 99.4%; Average loss: 2.8626
Iteration: 3975; Percent complete: 99.4%; Average loss: 2.5520
Iteration: 3976; Percent complete: 99.4%; Average loss: 2.7400
Iteration: 3977; Percent complete: 99.4%; Average loss: 2.7702
Iteration: 3978; Percent complete: 99.5%; Average loss: 2.3496
Iteration: 3979; Percent complete: 99.5%; Average loss: 2.6557
Iteration: 3980; Percent complete: 99.5%; Average loss: 2.6825
Iteration: 3981; Percent complete: 99.5%; Average loss: 2.4317
Iteration: 3982; Percent complete: 99.6%; Average loss: 2.7846
Iteration: 3983; Percent complete: 99.6%; Average loss: 2.6667
Iteration: 3984; Percent complete: 99.6%; Average loss: 2.6494
Iteration: 3985; Percent complete: 99.6%; Average loss: 2.5522
Iteration: 3986; Percent complete: 99.7%; Average loss: 2.3606
Iteration: 3987; Percent complete: 99.7%; Average loss: 2.7477
Iteration: 3988; Percent complete: 99.7%; Average loss: 2.4788
Iteration: 3989; Percent complete: 99.7%; Average loss: 2.5228
Iteration: 3990; Percent complete: 99.8%; Average loss: 2.7775
Iteration: 3991; Percent complete: 99.8%; Average loss: 2.4166
Iteration: 3992; Percent complete: 99.8%; Average loss: 2.6849
Iteration: 3993; Percent complete: 99.8%; Average loss: 2.7486
Iteration: 3994; Percent complete: 99.9%; Average loss: 2.6657
Iteration: 3995; Percent complete: 99.9%; Average loss: 2.5910
Iteration: 3996; Percent complete: 99.9%; Average loss: 2.8605
Iteration: 3997; Percent complete: 99.9%; Average loss: 2.5496
Iteration: 3998; Percent complete: 100.0%; Average loss: 2.5666
Iteration: 3999; Percent complete: 100.0%; Average loss: 2.6485
Iteration: 4000; Percent complete: 100.0%; Average loss: 2.6671

Run Evaluation

To chat with your model, run the following block.

# Set dropout layers to ``eval`` mode
encoder.eval()
decoder.eval()

# Initialize search module
searcher = GreedySearchDecoder(encoder, decoder)

# Begin chatting (uncomment and run the following line to begin)
# evaluateInput(encoder, decoder, searcher, voc)

Conclusion

That’s all for this one, folks. Congratulations, you now know the fundamentals to building a generative chatbot model! If you’re interested, you can try tailoring the chatbot’s behavior by tweaking the model and training parameters and customizing the data that you train the model on.

Check out the other tutorials for more cool deep learning applications in PyTorch!